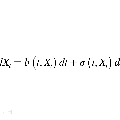Levy扩散过程与非局部偏微分方程

项目名称： Levy扩散过程与非局部偏微分方程

项目编号： No.11271294

项目类型： 面上项目

立项/批准年度： 2013

项目学科： 数理科学和化学

项目作者： 张希承

作者单位： 武汉大学

项目金额： 60万元

中文摘要： 本项目主要研究由Levy过程（特别地α稳定过程）驱动的随机微分方程与非局部积分偏微分方程。众所周知，Levy扩散过程的生成子为一非局部的积分偏微分算子，就像Brown扩散过程与二阶偏微分方程的联系一样，我们主要想探讨随机分析或者说概率的方法在非局部积分偏微分方程中的应用，反过来，通过研究非局部积分偏微分方程来研究带跳的随机微分方程。特别地我们主要侧重于以下几个方面的研究：1、拟线性积分偏微分方程的概率方法。2、由Levy过程驱动的随机微分方程的Krylov估计。3、非局部方程的Harnack不等式以及Holder估计。4、非局部积分偏微分方程的Lp理论。5、由Levy过程驱动的随机偏微分方程的遍历性。以上研究内容之间有着密切的联系。进一步，我们期望能应用到各种非线性问题中去，比方临界多维Burgers方程，准地转方程等等。

中文关键词： 非局部算子；Levy过程；随机微分方程；导数公式；遍历性

英文摘要： This project is mainly concentrated on stochastic differential equations driven by Levy processes (including α-stable processes) and nonlocal integro-differential equations. It is well-known that the generator of Levy diffusion process is an integro-differential (nonlocal) operator, like the relation between Brownian diffusion processes and second-order partial differential equations. We mainly want to use the stochastic analysis or probabilisitc techniques to study the problems in nonlocal integro-differential equations, and viceversa, by stduying the nonlocal equations, we want to solve the stochastic differential equations driven by Levy processes. In particular, we are mainly concerned with the following aspects: 1. Probabilistic approach for quasi-linear integro-partial differential equations. 2. Krylov's estimate for stochastic differential equations driven by Levy processes. 3. Harnack's inequality and Holder's estimate for nonlocal equations. 4. Lp-theory for nonlocal equations. 5. Ergodicity of stochastic partial differential equations driven by Levy processes. Among these problems, there are deep connections. After studying these problems, we expect to apply them to various nonlinear problems such as multidimensional critical Burgers equation and quasi-geostrophic equations etc.

英文关键词： Nonlocal operator；Levy process；stochastic differential equation；derivative formula；ergodicity