【NeurIPS2022】时序解纠缠表示学习

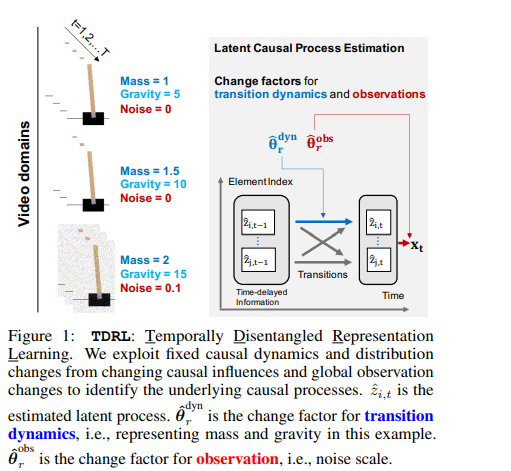
近年来，在无监督表示学习领域中，除了独立性之外，还通过利用类标签等侧面信息建立了因果相关潜变量解纠缠的强可识别性结果。然而，大多数现有的工作都受到函数形式假设(如独立源或进一步的线性过渡)和分布假设(如平稳、指数家族分布)的限制。如果潜在的潜在变量之间有任意的、非参数的因果影响，那么它们和它们的因果关系是否可识别是未知的。在这项研究中，我们从固定时间因果影响下的非线性混合中建立了非参数潜在因果过程的可识别性理论，并分析了分布变化如何进一步有利于解纠缠。我们提出了TDRL，这是一个原则性的框架，用于从平稳环境和不同分布位移下的测量序列数据中恢复时滞潜在因果变量并识别它们之间的关系。具体而言，该框架可以将未知分布位移分解为固定时变潜在因果关系下的跃迁分布变化，以及观测中观测变化下的跃迁分布变化。通过实验，我们表明延时的潜在因果影响被可靠地识别出来，我们的方法大大优于现有的基线，这些基线没有正确地利用这种变化的模块化表示。我们的代码可在以下网站获得:https://github.com/weirayao/tdrl。

https://www.zhuanzhi.ai/paper/69aeb6d5a927520a93b4b477e64e9cab