牛津大学等《多智能体系统的博弈论验证》最新论文，Rational verification: game-theoretic verification of multi-agent systems

摘要

我们对理性验证的最新技术进行了调查：检测给定时间逻辑公式 φ 是否在多智能体系统的部分或全部博弈论均衡中得到满足的问题——即系统是否会表现出行为 φ 表示假设系统内的智能体在追求他们的偏好时会理性地行事。在激励和介绍了理性验证的总体框架之后，我们讨论了过去几年取得的关键成果以及逻辑、人工智能和计算机科学方面的相关工作。

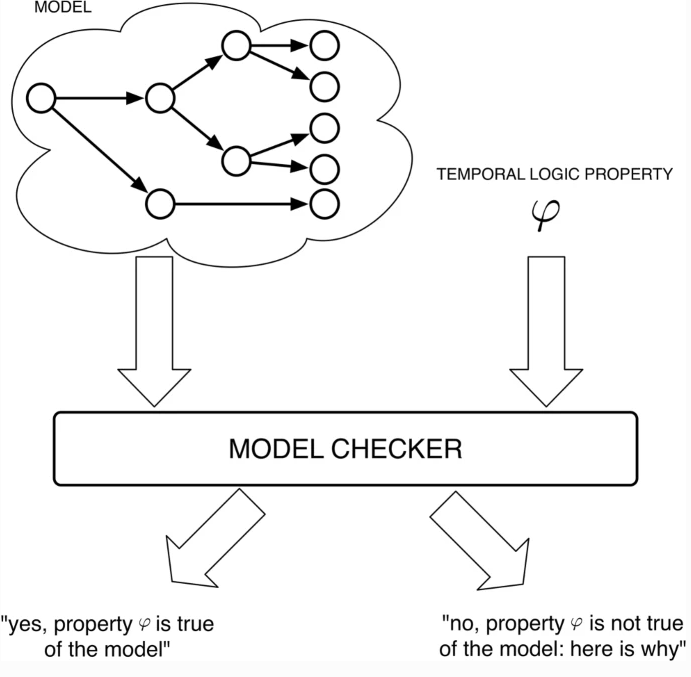
图1：模型检测。模型检测器将模型作为输入，该模型表示系统的有限状态抽象，以及关于系统行为的声明，以时间逻辑表示。然后它确定该声明是否适用于该模型；如果没有，最实用的模型检测器将提供一个反例

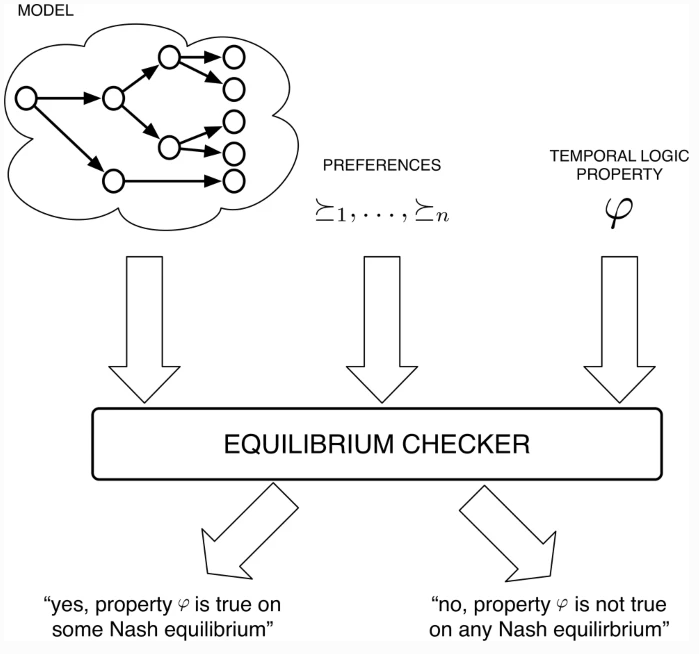
图2：均衡检测。模型检测的关键区别在于，我们还将每个系统组件的偏好作为输入，并且提出的关键问题是时间属性φ是否适用于系统的部分/全部均衡

引言

在过去十年中，人工智能技术在广泛的应用领域中的部署使验证此类系统的问题成为焦点。验证是计算机科学中最重要和最广泛研究的问题之一 [14]。验证是检测程序正确性的问题：与验证有关的关键决策问题是确定给定系统P是否满足给定规范φ. 当代最成功的验证方法是模型检测，其中系统的抽象有限状态模型表示为 Kripke 结构（标记的转换系统），规范表示为时间逻辑公式，即其模型旨在对应于系统的“正确”行为 [31]。然后，验证过程简化为确定 Kripke 结构是否满足规范公式，该过程可以在环境中实现自动化 [9,28]。

在本文中，我们将关注多智能体系统[73,82]。软件智能体最初是在 1980 年代后期提出的，但只是在过去十年中，软件智能体范式才被广泛采用。在撰写本文时，软件智能体无处不在：我们的手机中有软件智能体（例如，Siri），在线处理请求，在全球市场自动交易，控制复杂的导航系统（例如，自动驾驶汽车中的导航系统），以及甚至在家中代表我们执行任务（例如，Alexa）。通常，这些智能体不会孤立地工作：它们可能与人类或其他软件智能体交互。多智能体系统领域关注的是具有这些特征的理解和工程系统。

由于智能体通常由不同的委托人“拥有”，因此没有要求或假设委托给不同智能体的偏好以任何方式保持一致。他们的偏好可能是相容的，但也可能是相反的。博弈论提供了一个自然且被广泛采用的框架，通过该框架来理解具有这些属性的系统，参与者理性和战略性地追求他们的偏好 [61]，这一观察在过去十年中引发了大量研究，试图应用和将博弈论技术应用于多智能体系统的分析[63,73]。

研究问题

在本文中，我们关心的问题是我们应该如何思考多智能体系统中的正确性和验证问题（在这一点上，我们应该澄清，在这项工作中，我们只关心仅由软件智能体：在第 5节中，我们简要评论了验证智能体系统的问题）。

我们认为，在多智能体环境中，在智能体为追求他们的偏好而采取理性行动的假设下，询问系统将表现出什么样的行为是适当的。我们推进了多智能体系统的理性验证范式，作为经典验证的对应物。理性验证涉及确定给定的时间逻辑公式φ是否在多智能体系统的部分或所有博弈论均衡中得到满足——也就是说，系统是否会表现出系统在追求他们的偏好/目标时理性地行事。

我们首先详细描述我们方法的正确性和验证问题，以及用于验证的非常成功的模型检测范式。然后我们讨论了多智能体系统环境中正确性意味着什么，这导致我们引入理性验证和均衡检测的范式。在本次调查一系列用于理性验证的语义模型之后，总结了这些模型已知的关键复杂性结果，然后研究了用于理性验证的三个关键工具。最后，我们调查了当前研究的一些活跃领域。