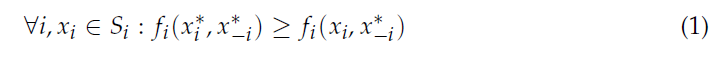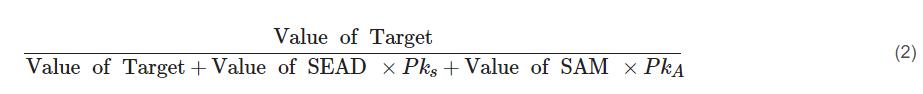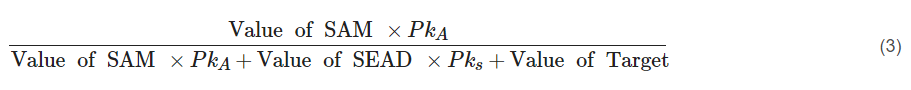万字长文!《博弈论在国防中的应用综述》悉尼大学与澳大利亚国防科技2022最新40页pdf综述论文
悉尼大学与澳大利亚国防科技最新《博弈论在国防中的应用综述》,值得关注!
【作 者】
Edwin Ho 1, Arvind Rajagopalan 2, Alex Skvortsov 3, Sanjeev Arulampalam 3, Mahendra Piraveenan 1*
1 悉尼大学工程学院
2 澳大利亚国防科技 (DST) 集团武器和作战系统部
3 澳大利亚国防科技 (DST) 集团海事部
关键词: 决策;博弈论;国防科学;地面战;海战;空战;跟踪;传感
1. 引 言
表 1. 本次综述中使用的分类系统
| 聚焦领域 | 智慧与控制战 | ||||
|---|---|---|---|---|---|
| 模式 | 传统(T) | 现代 (M) | |||
| 战域 | 地 (L) | 海 (S) | 空(A) | 赛博 (C) | 空间 (Sp) |
| 战争类型 | 资源分配战 (RAW) or 信息战(IW) or 武器控制战 (WCW) or 敌方监控战 (AMW) |
||||
| 博弈论分类1 | 非合作 (NCo) or 合作 (Co) |
||||
| 博弈论分类2 | 序贯 (Seq) or 同步 (Sim) |
||||
| 博弈论分类3 | 离散 (D) or 连续 (C) |
||||
| 博弈论分类4 | 零和(ZS) or 非零和 (NZS) |
||||
| Number of Players | 2人 (2P) or 3人(3P) or 多人(NP) |
||||
2.1 战争类型
-
资源分配战(RAW):为实现军事目标而进行的军事资源分配。 -
信息战(IW):操纵信息以实现军事目标。 -
武器控制战(WCW):控制武器以实现军事目标。 -
对手监控战(AMW):跟踪敌人的行为以实现军事目标。
2.2 战争领域
2.2.1 陆战
2.2.2 海战
2.2.3 空战
2.2.4 网络战
2.2.5 太空战
2.2.6 混合/其他战争
2.3 博弈论
2.3.1 纯策略与混合策略
博弈中的纯策略提供了玩家如何玩博弈的完整定义。玩家的策略集是该玩家可用的纯策略集 [10]。
2.3.2 纳什均衡
纳什均衡的概念是博弈论的基础。它是战略博弈中的一种状态(一组策略),就收益而言,没有参与者有动机单方面偏离。可以定义纯策略和混合策略纳什均衡。一个战略博弈通常可以有多个纳什均衡[7]。每个玩家可以从有限多个纯策略中进行选择的每个玩家数量有限的博弈在混合策略中至少有一个纳什均衡,这已被证明 [7]。
纳什均衡的正式定义如下。让 ( S, f ) 是一个有 n 个玩家的博弈,其中 Si 是给定玩家 i 的策略集。因此,由所有参与者的策略集组成的策略配置文件 S 将是,S=S1 × S2 × S3… × Sn。令 f(x)=(f1(x),…,fn(x)) 为策略集 x∈S 的支付函数。假设 xi 是参与者 i 的策略,x−i 是除参与者 i 之外的所有参与者的策略集。因此,当每个玩家 i∈1,…,n 选择策略 xi 时,策略集 x=(x1,…,xn),给特定玩家的收益 fi(x),这取决于该玩家选择的策略 (xi) 和其他玩家选择的策略 (xi-i)。如果任何单个参与者的策略单方面偏差都不会为该特定参与者带来更高的效用,则策略集 x∗∈S 处于纳什均衡[10]。正式地说,x∗ 处于纳什均衡当且仅当:
2.3.3 非合作博弈和合作博弈
通常,博弈被认为是为了玩家的自身利益而进行的,即使玩家合作,那也是因为在他们看来,在最大化玩家个人收益的情况下,合作似乎是最佳策略。在这样的博弈中,合作行为(如果出现)是由自私的目标驱动的,并且是短暂的。这些博弈可以称为“非合作博弈”。这些有时被称为“竞技博弈”,相当不准确。非合作博弈论是分析此类博弈的博弈论分支。另一方面,在合作博弈(有时也称为联盟博弈)中,玩家形成联盟或群体,有时是由于合作行为的外部强制执行,如果出现竞争,则在这些联盟之间发生竞争 [7,8, 9]。合作博弈使用合作博弈论进行分析,该理论预测将形成哪些联盟以及这些联盟的收益。合作博弈论侧重于联盟之间的盈余或利润分享[49],其中联盟通过形成联盟而得到一定的回报。通常,在系统中进行的合作博弈的结果等同于受限优化过程的结果 [50]。
2.3.4 零和博弈
零和博弈是一类所有参与者的收益总和为零的竞争博弈。在两人博弈中,这意味着一个玩家在收益中的损失等于另一个玩家在收益中的收益。因此,两人零和博弈可以用一个只显示一个玩家的收益的收益矩阵来表示。零和博弈可以用 mini-max 定理来解决 [51],它指出在零和博弈中,有一组策略可以最小化每个玩家的最大损失(或最大化最小收益)。这种解决方案有时被称为“纯鞍点”。可以说股市是一场零和博弈。相比之下,大多数有效的经济交易都是非零和的,因为每一方都认为,它收到的东西(对自己)比它分享的东西更有价值[10]。
2.3.5 完美与不完美的信息博弈
在一个完美的信息博弈中,每个玩家都知道所有其他玩家之前行为的完整历史,以及博弈的初始状态。在不完全信息博弈中,部分或所有玩家无法获得关于其他玩家先前行为的全部信息 [52,53]。
2.3.6 同步博弈和序贯博弈
同步博弈要么是正常形式的博弈,要么是扩展形式的博弈,在每次迭代中,所有玩家同时做出决策。因此,每个玩家都被迫在不知道其他玩家(在该迭代中)做出的决定的情况下做出决定。相反,顺序博弈是一种广泛形式的博弈,其中玩家以某种预定义的顺序做出决定(或选择他们的策略) [52,53]。例如,如果一方总是有权提出第一个要约,而另一方在此之后提出要约或还价,则可以将谈判过程建模为顺序博弈。在顺序博弈中,至少有一些玩家可以在做出自己的决定之前观察到其他玩家的至少一些动作(否则,即使玩家的动作在时间上没有同时发生,博弈也会变成同时博弈)。然而,对于给定的玩家来说,前一个玩家的每一个动作并不是必须要观察到的。如果一个玩家可以观察到每个前一个玩家的一举一动,那么这种顺序博弈就具有“完美信息”。否则,已知博弈具有“不完美信息”[10]。
2.3.7 差异博弈
微分博弈通常是广泛形式的博弈,但它们不是具有离散的决策点,而是在连续的时间范围内建模 [10]。在这样的博弈中,每个状态变量根据微分方程随时间连续演化。此类博弈非常适合模拟快速发展的防御场景,其中每个玩家都参与了某些参数的自私优化。例如,在导弹跟踪问题中,追击者和目标都试图控制它们之间的距离,而追击者不断地试图缩小这个距离,而目标不断地试图增加它。在这种情况下,决策的迭代轮次过于离散,无法对每个玩家的连续运动和计算进行建模。微分博弈是模拟此类场景的理想选择。
2.3.8 共同兴趣博弈
共同兴趣博弈是另一类非合作博弈,其中有一个所有玩家都严格比所有其他配置文件更喜欢的动作配置文件[52]。换句话说,在共同利益博弈中,玩家的利益是完全一致的。可以说,共同利益博弈是零和博弈的对立面,在这种博弈中,玩家的利益是完全对立的,因此一个玩家的财富增加必然导致其他玩家的财富集体减少。共同利益博弈最初是在冷战政治的背景下研究的,以理解和规定处理国际关系的策略[54]。因此,将非合作博弈分为共同利益博弈和非共同利益博弈是有意义的,就像将它们分为零和博弈和非零和博弈一样有意义,因为这两个概念(零和博弈和共同利益博弈)代表了非合作博弈的极端情况。
2.3.9 信号博弈
信号博弈 [52] 是一种不完全信息博弈,其中一个玩家拥有完美信息,而另一个则没有。拥有完全信息的玩家(Sender S)通过信号将消息传递给其他玩家(Receiver R),其他玩家在推断出隐藏在消息中的信息后会根据这些信号采取行动。发送者S有几种可能的类型,其中博弈中的确切类型t对接收者R来说是未知的。t决定了S的收益。R只有一种类型,并且两个玩家都知道该收益。
博弈分为发送阶段和表演阶段。S 将发送 M={m1,m2,m3,…,mj} 消息之一。R 将接收该消息并以集合 A={a1,a2,a3,…,ak} 中的操作进行响应。每个玩家收到的收益取决于发送者的类型和消息的组合,以及接收者响应的操作。信号博弈的一个例子是 Beer-Quiche 博弈 [52],在该博弈中,接收者 B 选择是否与玩家 A 决斗。玩家 A 要么乖巧要么懦弱,而玩家 B 只想与后者。玩家 A 选择早餐吃啤酒或乳蛋饼。虽然他们更喜欢乳蛋饼,但乳蛋饼从刻板印象中发出信息,即吃乳蛋饼的人很懦弱。玩家 B 必须根据玩家 A 选择的早餐,分析每个决定(决斗或不决斗)如何给他们带来更好的回报。
2.3.10 行为博弈论
行为博弈论将经典博弈论与实验经济学和实验心理学相结合,从而放宽了经典博弈论中许多不切实际的简化假设。它偏离了简化假设,例如完美理性 [55]、独立公理,以及不考虑将利他主义或公平作为人类决策动机的假设 [56,57]。我们将在这篇评论中展示与行为博弈论相关的方法对于模拟军事场景(例如信号博弈)至关重要。
2.3.11 进化博弈论
进化博弈论是将博弈论应用到进化生物学领域的结果[58]。进化博弈论中提出的一些关键问题包括:哪些种群/策略是稳定的?在其他策略盛行的人群中,哪些策略可以“入侵”(变得流行)?在重复的博弈设置中,玩家如何回应其他玩家获得或被认为正在获得更好的回报?进化博弈通常被建模为迭代博弈,其中一群玩家在混合良好或空间分布的环境中迭代地玩相同的博弈。
如果一种策略在流行时有可能阻止任何突变策略渗透其环境,则可以将其识别为进化稳定策略 (ESS)。或者,ESS 是一种策略,如果在给定环境中被人群采用,则不会被任何替代策略入侵。因此,玩家从 ESS 切换到另一种策略没有任何好处。因此,本质上,ESS 确保了扩展的纳什均衡。为了使策略 S1 成为对抗另一个“入侵”策略 S2 的 ESS,就预期收益 E 而言,需要满足下面提到的两个条件之一。
E(S1,S1)>E(S2,S1):通过单方面改变策略到 S2,玩家将输给另一个坚持 ESS S1 的玩家。
E(S1,S1)=E(S2,S1) & E(S1,S2)>E(S2,S2):一个玩家,通过转换为 S2,对另一个坚持 ESS S1 的玩家既不赢也不输,但是与已经“转换”到 S2 的玩家对抗,玩家最好玩 ESS S1。
如果满足这两个条件中的任何一个,则新策略 S2 无法入侵现有策略 S1,因此,S1 是针对 S2 的 ESS。进化博弈通常被建模为迭代博弈,即群体中的玩家迭代地玩相同的博弈[52]。
三、博弈论在国防科技应用中的应用
如前所述,在博弈建模防御场景中影响收益矩阵的主要参数是目标的价值、资源的价值和目标的优先级。除此之外,国防应用程序中使用的博弈可能会有很大差异,我们将在下面看到。因此,本节的结构基于每篇论文所涵盖的领域(战争类型)。如果一篇论文涵盖多个领域,则将其包含在最相关的小节/领域中。然而,我们详细分析了每篇论文所使用的博弈类型、收益函数的结构方式、可用策略和均衡等。
3.1 研究 陆战 的论文
在博弈论的陆战相关应用中,大多数研究都集中在防御战上,即军方决定如何最好地将地面防御分配给多种威胁。一些研究还关注历史上的陆上冲突,并在事后提供博弈论分析,揭示了在历史冲突中凭直觉做出的一些决定如何具有理性和数学上的合理性。陆战可能导致非常严重的人员伤亡,因此了解如何最大限度地减少人员损失是陆战的关键组成部分(尽管不是唯一目标)。很多时候,优先考虑军事资源也是成功的基础,并且经常在战略决策中占据突出地位。此外,通常在涉及地面战的场景中,评估有关对手、他们可能的战术或地形的知识很重要:可能需要与在某些地方部署的空降部队作战,或者可能需要穿越不确定的领土。在每一种情况下,了解一支部队的信息不完善之处将有助于该部队做出理性的决定。
几篇论文使用博弈论来模拟当前和历史背景下的陆战。比尔等人[65] 设计一个博弈,以最好地将防御资源分配给一组需要保护的位置/资源。然后攻击者必须决定他们如何选择分裂他们的力量来攻击不同的目标。该博弈被建模为正常形式的两人博弈。这个博弈的收益是绝对的,对位置 i 的攻击要么成功,要么失败,攻击者获得 ai,防御者失去 di。由于攻击命令是在攻击之前确认的,因此攻击者必须使用一组纯策略。博弈既可以同时进行,也可以依次进行。也就是说,可以根据攻击者在做出决定之前是否知道防御者如何分配他们的资源来玩博弈。这导致了一个理想的战略,即让一些目标不设防,并通过让一些地区易受攻击来加强关键地区的防御。
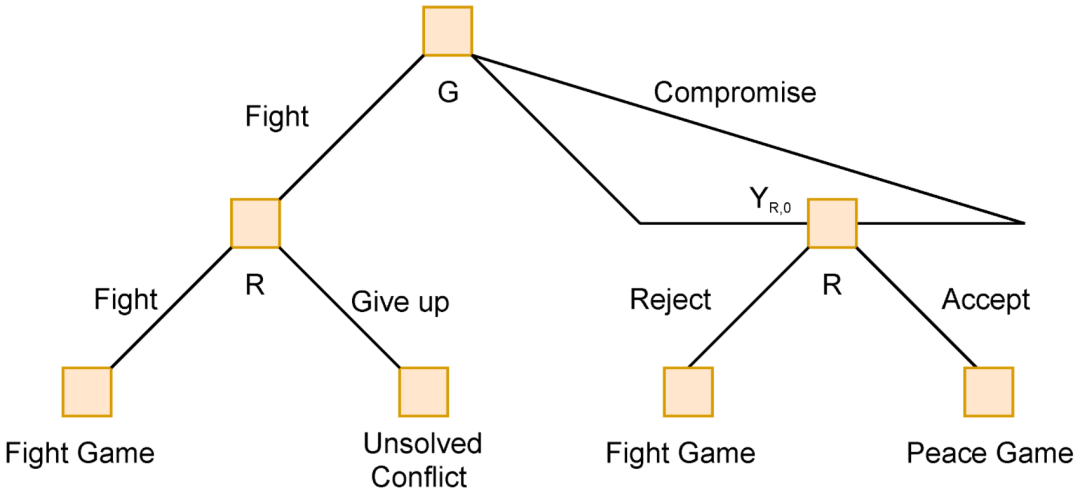
我们审查的下一篇论文是 Gries 等人[66] 这是对博弈论原理在游击战/破坏稳定战中的效用的全面调查。他们建模的重要因素是:破坏稳定的叛乱分子经常随机攻击,造成持续的威胁,必须有持续的缓解和检测策略;战争的持续时间很重要,并且会改变分配给目标和资产的价值;时间偏好在确定优先事项方面起着至关重要的作用,因为价值判断决定了战略决策,而战略决策又决定了成功或失败。他们提出的博弈模型既包括顺序非合作博弈,也包括同时非合作博弈,其中两个参与者分别是游击队和政府。对于这些冲突,经济和社会影响比军事损失和收益更重要,因此在计算结果价值方面发挥着更重要的作用。博弈特别模拟了双方试图寻求和平或与对方发生冲突的时刻。在这些时刻,政府军必须考虑每种选择的财务成本,而叛军则检查交战的优先顺序,以及他们将为每次交战提供多少战斗力。图 1 展示了从破坏稳定战争的这些时刻出现的决策树示例,其中 G 代表政府决策,R 代表叛军决策。
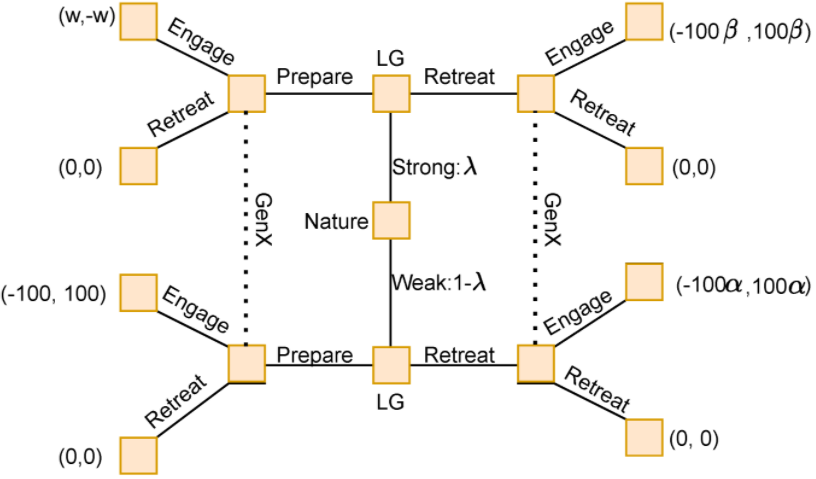
图 2. 100 Horsemen 信号博弈 [68]
在图 2中:
LG代表汉军李广将军的决策点。
GenX代表了敌对匈奴势力的决策点。
收益被列为(LG,GenX)
λ∈(0,1) 代表将军的能力,
α 和 β 代表在撤退中丧生的汉族骑兵比例
w 是一个正参数
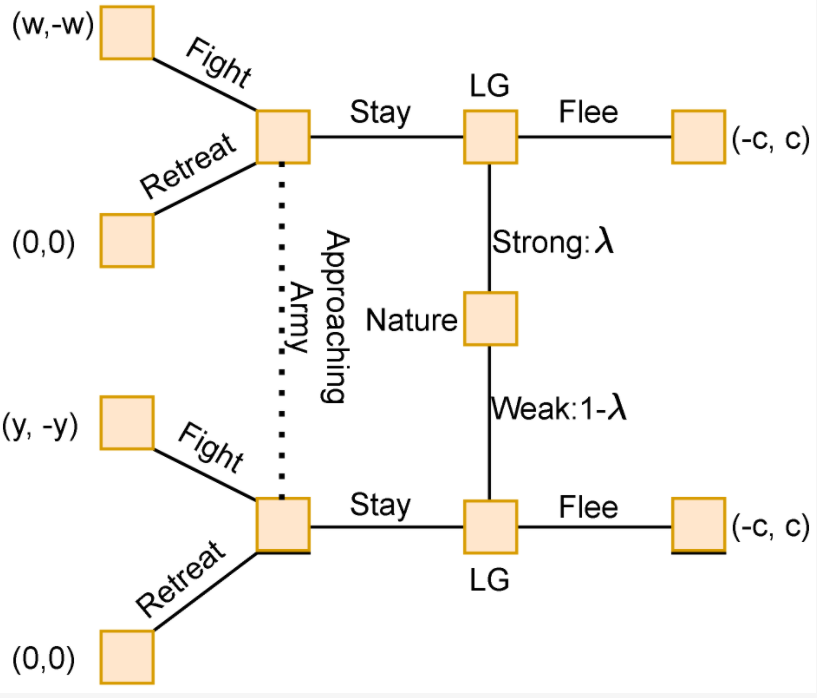
第二场比赛与第一场非常相似。在这个博弈中,一座小城由强大的诸葛亮将军守卫。他得知一支强大的敌对军队正在接近这座城市。他面临两个选择。他可以逃跑,然后他会脱离城市,很可能会被接近的军队追杀,或者他可以留下来保卫城市。如果他选择了后者,大军出手,他很可能会失去性命、军队和城市。面对这种困境,他命令他的手下隐藏起来,让城市从外面看起来空无一人。他爬到城市最重要的塔顶,演奏音乐。对方将军知道梁将军的经验和实力,怀疑将军在空城的塔楼中采取这种不起眼的位置来伏击他的军队,他们离开了城市以避免被伏击。梁将军在这里有效地发出了两个信号。首先是他的声誉,这是一个包含他的战略和军事实力的信号。第二个是他选择留下来保卫这座城市。有了这两条信息,梁将军的军队的行踪和规模就没有了,对方军队选择了零损失的安全选项,离开了。这段历史被建模为另一个两人信号博弈,如下图 3 所示:
在图 3 中:
ZL代表诸葛亮将军的决策点
收益被列为(ZL,反对军)
λ∈(0,1) 代表将军的能力,
c代表城市的价值
w 代表 ZL 的军队与对方军队匹配时的收益
y表示ZL的军队比对方军队弱时的损失,并且y>c因为它包括失去城市
这两段历史都代表了面对近乎确定的失败时做出的杰出军事决策,实际上是将军们对信号的细微差别有深刻理解的例子,并在战略互动中做出理性决策,迫使他们取得有利于自己的结果。
3.2 研究 海战 的论文
令人惊讶的是,直接和主要使用博弈论处理海战的论文相对较少,尽管海战在人类历史上比空战早了相当大的优势。莱文 [69] 使用博弈论的概念研究过去几个世纪海战的各个方面。在 18 世纪和 19 世纪,当时的强国建造了军舰,并在其两侧放置了大炮。这意味着船只通常只能从侧面攻击。当作为无敌舰队航行时,标准的做法是形成“战线”,即一列盟军海军舰艇朝一个方向航行,使他们的两侧面向敌人,也排成一条线。两个平行的对立舰队然后可以用大量的大炮互相攻击。“战线”战略被认为是纳什均衡,因为任何一支舰队都不会从掠夺中获益(这是当时的一种战术,攻击舰船会试图驶过对手的船尾,在那里集中炮火,而由于船尾的大炮位置较少,敌人只能做出最低限度的反应。攻击舰会损坏对手的船尾和一些舷侧)。根据莱文 [69 ] 倾斜在舰队中不是首选,因为这意味着必须先在敌人前面航行,然后转向它——当船只的速度大致相等且机动困难时,这是一项具有挑战性的任务。由于两支舰队都不会从转向敌人中获益,也不会取得领先,莱文得出的结论是,这种策略——形成一条战线并与另一支舰队平行航行——是每个舰队的最佳反应,因此代表了纳什均衡。
莱文接着提到了英国舰队偏离上述战略并正交驶向法国和法国-西班牙舰队的战斗。在莱文提到的第一场战斗中,这很可能是无计划的。第二次是 1805 年的特拉法加海战,这是经过精心设计的:英国舰队将自己分成两列,每列都垂直于法西线航行,扫射了大约 45 分钟,然后坠毁并开始了一场一般混战。英国人将继续孤立法西舰队的中部,以取得决定性的胜利。莱文认为这两场战斗都是他论文的反例。然而,在特拉法加战役中,英国的战略可能是对可能的法西战略形成正统战线的最佳回应。英国海军上将,纳尔逊勋爵希望阻止法西舰队逃跑——如果两支舰队形成平行战线,他们可以逃跑——从而减少了他将自己的舰队组成战线所获得的奖励。此外,他可能估计法国和西班牙舰船的低劣炮火会减少扫射的效果,从而减少他直接向法西舰队冲锋所获得的负面回报。在他看来,与正统的战线相比,这可能使非正统的选择成为对可能的法西战略的更好回应。虽然莱文没有明确地将这些战略在那个时代的海战中归因于博弈论,但所采用的策略仍然可以通过博弈论分析来证明:这是博弈论“直观”应用的一个例子,而没有正式研究它。
Maskery 等人2007 (a) [70] 研究使用网络使能作战 (NEOPS) 框架部署反舰导弹反措施的问题,其中多艘舰船进行通信和协调以防御导弹威胁。在这里,导弹威胁被建模为离散马尔可夫过程,它们出现在固定物理空间内的随机位置,并按照一些已知的目标动力学和制导规律向舰船移动。配备有诱饵和电磁干扰信号等对抗措施(CM)的船舶被建模为瞬态随机博弈的玩家,其中个体玩家的行为包括使用 CM 最大限度地提高自身安全,同时与其他基本上旨在实现相同目标的参与者。这个博弈论问题的最优策略是一个相关的均衡策略,并且证明是通过一个具有双线性约束的优化问题来实现的。这与纳什均衡解提出的 tepmaskery2007 分散到一个相关问题但没有玩家协调的问题形成对比。本文的一个值得注意的贡献是,它还量化了实施 NEOPS 均衡策略所需的沟通量。本文强调了博弈论方法在分析现代战争中至关重要的网络系统中的最优策略中的实用性。这与纳什均衡解提出的 tepmaskery2007 分散到一个相关问题但没有玩家协调的问题形成对比。本文的一个值得注意的贡献是,它还量化了实施 NEOPS 均衡策略所需的沟通量。本文强调了博弈论方法在分析现代战争中至关重要的网络系统中的最优策略中的实用性。这与纳什均衡解提出的 tepmaskery2007 分散到一个相关问题但没有玩家协调的问题形成对比。本文的一个值得注意的贡献是,它还量化了实施 NEOPS 均衡策略所需的沟通量。本文强调了博弈论方法在分析现代战争中至关重要的网络系统中的最优策略中的实用性。
在 [71],Maskery等人2007(b)考虑以网络为中心的部队保护一个任务组免受反舰导弹的问题。该模型中的决策者是配备硬杀伤/软杀伤武器(反措施)的舰船,这些舰船也被认为是博弈论环境中制定该问题的参与者。这些平台必须独立地就反措施的最佳部署做出关键决策,同时它们同时朝着保护任务组成员的共同目标努力。本质上,这是海军环境中分散的导弹偏转问题,它被表述为一种瞬态随机博弈,舰艇可以计算出一个处于纳什均衡的联合反措施策略。在这里,船只相互玩博弈,而不是使用导弹。这种方法自然适用于分散的解决方案,当完全通信不可行时可以实施。此外,该公式导致将该问题解释为已知存在纳什均衡解的随机最短过去博弈。
Bachmann等人[72] 使用非合作的两人零和博弈分析雷达和干扰机之间的相互作用。在他们的方法中,雷达和干扰机被认为是具有相反目标的“参与者”:雷达试图最大化检测到目标的概率,而干扰机试图通过干扰来最小化雷达的检测。Bachmann等人。[ 72] 假设存在瑞利分布杂波时的 Swerling Type II 目标,针对不同干扰情况下的单元平均 (CA) 和阶数统计 (OS) CFAR 处理器描述了某些效用函数。这种博弈论公式是通过优化这些效用函数来解决的尺寸。由此产生的矩阵形式的博弈被求解为雷达和干扰机的最佳策略,他们从中确定雷达和干扰机有效实现其各自目标的条件。
3.3 研究 空战 的论文
空战通常是一种正常形式的博弈,根据对武器库不同要素强度的假设和知识,在交战之前就使用资源做出决定。例如,压制敌方防空车辆(SEAD)对地对空防御和地对空导弹(SAM)有效,但对战斗机无效。因此,当军事人员决定在一场交战中使用哪些资源时,他们需要权衡每项资源的价值,以及目标对冲突双方的重要性。如果攻击部队对目标的重视程度远高于其实际价值,那么他们增加的资源支出可能对其整体军事行动不利。人类通常操作空中武器,
以博弈论为模型的空战文献有限。汉密尔顿 [73] 为博弈论在多种空战情况下的应用提供了综合指南。汉密尔顿建议使用博弈论来设计战略,不仅要基于自己的军事选择,还要基于对敌人行动的预期。博弈论解释了与敌人的不同互动,而不是简单地考虑哪一方拥有更大的最大努力力量。如今,许多军队可以适应瞬息万变的形势,根据新形势调整行动。因此,汉密尔顿建议首先确定双方可用的所有战术选项。如前所述,将博弈论用于军事的最基本要素之一是准确了解每项资产的价值——详细说明双方的库存和战略可能性将最好地阐明所有战略选择。对于每个选项,汉密尔顿建议分配一个数值——有效性度量 (MoE)。关于教育部的决策很重要,因为对教育部的准确判断将支持战略性选择。不正确的教育部可能导致不正确的战略决策,也可能导致对决策错误原因的理解不足。这方面的一个例子(尽管不是在空战背景下)是越南战争,美国早期的战略是最大限度地压制越共士兵。由于北越领导层没有非常重视他们的步兵,美国的战略最终导致了战争的失败。接下来,汉密尔顿建议计算冲突双方策略之间所有可能相互作用的组合值。这将产生一个收益矩阵,从中可以得出每个参与者的最优或优势策略,然后是一个均衡解决方案。因此,在军事领导人可能参与的任何交战之前,他们对博弈的预期结果有一个完整的概念。汉密尔顿在这些指导方针中添加的一个警告是从整体上考虑军事行动的长度。如果替换成本低或数量多,可为一场战斗或打击攻击分配给资源的值可能很小。但是,根据整个战役中此类冲突的数量,这些资源可能变得至关重要。
为了说明这些观点,汉密尔顿将它们应用于 SEAD 和时间关键目标的标准空战博弈。在这场战斗中,“蓝方”试图消灭一些地面目标。为此,他们使用 SEAD。作为回应,“红方”将发射 SAM,这是 SEAD 难以避免的。然而,在预料到这种反应的情况下,蓝方也拥有可以防御 SEAD 并抵消 SAM 但无法攻击目标的攻击机。蓝队的问题是:目标的价值是多少,应该为目标部署多少比例的 SEAD 和攻击机?同样,对于红队来说:目标的价值有多大,应该解雇多少(如果有的话)SAM?汉密尔顿认为,最佳的红方策略是只为一小部分交战开火,这等于:
最优蓝色策略是将部分飞机分配为SEADs,等于:
在这里,
Pks 是 SAMS 摧毁 SEAD 的概率
PkA 是攻击机摧毁 SAM 的概率
鉴于飞机和导弹发射的每一种可能分配,这个公式对交战的可能结果给出了简明的预测。必须指出的是,在实践中要准确量化不同目标和资源的数值是非常困难的。
Garcia等人2019 [74] 调查保卫海上海岸线免受两架敌机攻击的问题,两架敌机的主要目标是入侵防御飞机控制的领土。另一方面,防御者试图通过尽可能远离边界连续拦截两架敌机来防止这种情况发生。这是一个典型的追逃场景,代表了机器人、控制和防御领域的许多重要问题。在本文中,Garcia等人,地方连续捕获两个攻击者/逃避者,而攻击者在面对之前合作并最小化他们与边界的组合距离。Garcia等人,然后通过求解一组非线性方程,找到攻击者和防御者的最优策略。本文讨论的合作策略为能力较弱(可能较慢)的代理在执行任务时提供了一种重要的协调方法。
Garcia等人2017 [75] 考虑一个空战场景,其中被攻击导弹交战的目标飞机利用防御导弹来保护自己,因为它试图通过最大化自身与攻击者之间的距离来逃脱攻击者,而防御者尽可能靠近它攻击导弹。该博弈被称为主动目标防御差异博弈(ATDDG)。在这篇论文中,作者扩展了之前在这个三方问题上所做的工作,为 ATDDG 开发了一种封闭形式的分析解决方案,如果防御者导弹进入指定半径 rc > 0 的捕获圈内,则防御者导弹可以击败攻击者。此外,尽管攻击者采用了未知的制导律,而不是假设它是比例导航(PN)或追踪(P),但论文中展示的封闭形式的最佳状态反馈解决方案应该可以工作。最后,作者为目标飞机提供了一组初始条件,如果目标防御团队在攻击导弹采用未知制导法则的情况下发挥最佳作用,则目标飞机的生存得到保证。
Deligiannis等人[76] 考虑在存在多个干扰器的情况下多输入多输出 (MIMO) 雷达网络中的竞争功率分配问题。雷达网络的主要目标是最小化雷达发射的总功率,同时为每个目标实现特定的检测标准。在这个问题中,雷达面临着智能干扰机,这些干扰机可以观察雷达发射功率,从而决定其干扰功率,以最大限度地干扰雷达。Deligiannis等人,将此功率分配问题视为非合作博弈,其中参与者是中央雷达控制器和干扰机,并使用凸优化技术解决此问题。此外,它们为这种情况下纳什均衡的存在性和唯一性提供了证据,
同样,He等人[77]考虑多基地雷达网络中的雷达对抗问题,在智能干扰器存在的情况下研究联合功率分配和波束成形的博弈论公式。该网络中每个雷达的目标是满足目标的预期检测性能,同时最小化其总发射功率并减轻潜在干扰。另一方面,干扰机的目标是调整自己的发射功率来干扰雷达,以保护目标不被检测到。首先,He等人研究功率分配博弈,每个玩家(雷达和干扰器)的策略集由他们各自的发射功率组成。然后他们着手解决相应的优化问题,得出雷达和干扰机的最佳响应函数,并证明纳什均衡的存在性和唯一性。接下来,他们再次将存在干扰时的联合功率分配和波束形成器设计问题视为非合作博弈,并提出了一种功率分配和波束形成算法,该算法被证明可以收敛到其纳什平衡点。
McEneaney等人[78] 研究无人驾驶飞行器 (UAV) 针对地面目标和防御单位(如地对空导弹 (SAM) 系统)的指挥和控制问题。这项工作的动机源于无人驾驶空中作战场景中对作战计划和实时调度的要求。该问题被建模为蓝色玩家 (UAV) 和红色玩家之间的随机博弈,包括 SAM 和地面目标。每一方都可以有许多目标:例如,一名蓝色玩家可能会尝试摧毁一个战略目标,同时尽量减少对自己的伤害。另一方面,红色玩家可能会试图对无人机造成最大的伤害,同时保护自己免受无人机的攻击。
无人机的控制策略由一组离散变量组成,这些变量对应于要攻击的特定目标或 SAM,而 SAM 的控制策略是“打开”或“关闭”雷达。请注意,当雷达“开启”时,SAM 对蓝色玩家造成伤害的概率会增加,蓝色玩家对 SAM 造成伤害的概率也会增加。这个随机博弈的解是通过动态规划获得的,并用一些数值例子来说明。这项工作的主要贡献是分析了一种基于风险敏感控制的方法,用于不完全信息下的随机博弈。特别是,这种方法不仅可以处理由于随机噪声引起的噪声观察,还可以处理在观察中包含对抗性成分的情况。
Wei等人[79] 开发了一个任务决策系统,用于多个无人作战飞行器 (UCAV) 协同工作。UCAV的武器是空对空导弹。在论文中,一支由一架无人驾驶战斗轰炸机组成的红色-UCAV 小组,两侧是两架 UCAV,试图打击一个蓝色小组的地面目标。蓝队拥有自己的一套 UCAV,旨在击败红队。给定导弹对抗其选定威胁的成功取决于攻击者与威胁之间的距离、它们的相对速度和相对角度。该场景被表示为同时正常形式的博弈,团队的策略对应于蓝队实体与红队实体的分配,反之亦然。在论文中,红队或蓝队的回报是基于考虑给定分配的有效性,这又取决于对方球队分配分组之间的相对几何形状。Dempster-Shafer (DS) 理论适用于利用 DS 组合公式来制定收益的情况。这些为每个策略计算的收益为每个团队然后放入双矩阵,即每个团队一个,并使用线性规划优化方法求解。如果不存在最优纳什均衡,则应用并解决混合策略方法。然后,作者开发了一些具有不同几何形状的任务场景,并说明了他们的博弈论分配策略的使用。他们使用包含红色和蓝色团队的实体几何注释图来证明由他们的收益公式确定的分配策略是令人满意的。
Ma等人[80] 开发了一种博弈论方法,为在超视距 (BVR) 空战对抗中相互交战的多个无人机 (UAV) 团队生成协作占用决策方法。超视距作战之所以成为可能,是因为导弹技术的发展能够实现远程交战。在论文中,每一方的团队首先决定其无人机实体的占用位置(笛卡尔空间中的立方体),然后为每个无人机团队成员选择参与的目标。目标是让每一方都获得最大的优势,同时经历最小的威胁条件。应用零和同时双矩阵博弈来分析问题。对于给定的无人机占用率,考虑射程和武器最小/最大性能标准的高度和距离优势公式用于生成效用函数的收益值。随着博弈的规模随着每个团队的占用立方体和无人机数量的增加而导致规模(以及策略)的爆炸式增长,作者选择增强旨在解决大型问题的双 Oracle (DO) 算法通过将其与邻域搜索 (NS) 算法结合到双 Oracle 邻域搜索 (DO-NS) 中来缩放早期作品中的零和博弈问题。通过仿真,作者说明结果表明 DO-NS 算法在计算时间和解决方案质量方面优于 DO 算法。随着博弈的规模随着每个团队的占用立方体和无人机数量的增加而导致规模(以及策略)的爆炸式增长,作者选择增强旨在解决大型问题的双 Oracle (DO) 算法通过将其与邻域搜索 (NS) 算法结合到双 Oracle 邻域搜索 (DO-NS) 中来缩放早期作品中的零和博弈问题。通过仿真,作者说明结果表明 DO-NS 算法在计算时间和解决方案质量方面优于 DO 算法。随着博弈的规模随着每个团队的占用立方体和无人机数量的增加而导致规模(以及策略)的爆炸式增长,作者选择增强旨在解决大型问题的双 Oracle (DO) 算法通过将其与邻域搜索 (NS) 算法结合到双 Oracle 邻域搜索 (DO-NS) 中来缩放早期作品中的零和博弈问题。通过仿真,作者说明结果表明 DO-NS 算法在计算时间和解决方案质量方面优于 DO 算法。通过将其与邻域搜索 (NS) 算法结合到双 Oracle 邻域搜索 (DO-NS) 中。通过仿真,作者说明结果表明 DO-NS 算法在计算时间和解决方案质量方面优于 DO 算法。通过将其与邻域搜索 (NS) 算法结合到双 Oracle 邻域搜索 (DO-NS) 中。通过仿真,作者说明结果表明 DO-NS 算法在计算时间和解决方案质量方面优于 DO 算法。
Başpınar、Barış等人的工作[81] 专注于使用基于优化的控制和博弈论方法对两架无人机 (UAV) 之间的空对空作战进行建模。在这项工作中,车辆运动用特定变量表示,并且通过确定满足平坦输出空间中定义条件的平滑曲线来解决从一个航路点移动到另一个航路点的任何轨迹规划。确定后,所有涉及描述平滑曲线的变量都可以恢复到原始状态/输入空间。其影响是通过减少所需变量的数量来加速解决任何轨迹优化。然后利用博弈论,将两架无人机之间的空战建模为使用极小极大方法的零和博弈。那是,当对手采取最佳策略时,每一方都试图最大化其收益。在这里,目标是让每架无人机直接落后于另一方,并在满足机载武器有效射程限制的射程阈值内。
在 [81],作者提供了与基于方位角和方位角追尾目标的程度相关的成本函数,以及当对手处于最佳射击范围的某个阈值内时与生成最大得分相关的成本函数. 成本函数相乘以创建总成本。成本函数被放入后退水平控制方案中,其中通过选择控制确定的轨迹规划在给定的前瞻时间段内执行,其中两个参与者都使用相反的策略。每个玩家都将其对手视为视野内的可到达集合,并使用它来选择其控制选择以最大化其收益。这个过程每隔几个控制步骤就重复一次。与该领域的大多数其他作品不同,作者在性能包络内使用全套控制输入而不是一个子集(例如,转弯、保持倾斜、以特定角度向左滚动、伊梅尔曼转、分裂S或螺旋俯冲),因此指出生成更优化的解决方案对于每个玩家的策略。提供了两种模拟场景,第一种情况是无人机从空中优势位置开始,然后执行后退地平线成本函数优化以在最佳射程内与对手进行尾追。作者表明,应用控制时的速度、负载系数和坡度角在飞行期间不会违反界限,并且会生成可行的轨迹。对于第二次模拟,无人机最初处于追尾状态,但不满足射程内标准。当追赶者继续追赶时,被追赶的对手通过应用成本函数进行机动逃跑。在交战结束时,满足射击范围标准并且目标直接在前方但处于次优方位,这导致其逃跑。这些场景用于证明所开发的控制策略的有效性,从而为两架相互交战的无人机提供战斗策略的自动选择。
Casbeer等人[82],考虑这样一种情况,其中一个攻击者导弹追击一个无人驾驶飞行器目标,两枚防御导弹从与目标结盟的实体发射,并与目标合作。它延伸自典型的三方博弈场景,其中只有一枚防御导弹与攻击者合作,与目标合作。作者在这里将其称为主动目标防御差异博弈(ATDDG)。除了在 ATDDG 的扩展中计算玩家的最优策略外,本文还试图确定目标在使用两名防御者而不是一名防御者时降低脆弱性的程度。制定了一个约束优化问题来解决这种情况。结果表明,通过选择与任一防御者合作,目标可以更成功地逃脱攻击者。此外,两个防御者的存在使攻击者更容易被拦截。当两枚防御者导弹处于有利位置时,两者都可以拦截攻击者。
Han等人 [83] 提出了一个综合空中和导弹防御 (IADS) 问题,其中配备拦截导弹 (IM) 的地对空导弹 (SAM) 电池与攻击者导弹 (AM) 攻击目标城市。该问题被视为具有完全信息的简化的两方零和博弈,具有三个阶段。这三个阶段对应于防御者将 SAM 分配给城市,随后攻击者将导弹齐射分配给城市,最后防御者分配拦截导弹以反击攻击者导弹齐射。在这个问题中所做的简化假设是在城市附近只分配了一个 SAM,每个站点只安装一个。此外,对每枚攻击导弹发射的拦截器不超过一个。此外,一个 DM 只能分配一个 IM,每个 SAM 具有相同数量和类型的 IM,并且 AM 是相同的,并且在一次齐射中发射。尝试使用扩展形式博弈树、α-β 剪枝和对需要保护的六城市网络使用双 Oracle (DO) 算法来解决三级博弈。DO 算法是一种启发式算法,不能保证找到完美子博弈纳什均衡 (SPNE)。研究了每种算法选择达到子博弈完美纳什均衡的效率。对于博弈树方法,得出的结论是,由于问题的组合性质,策略空间的大小被确定为增加到难以处理的大小。在应用 α-β 剪枝时,与 DO 算法相比,本文确定确定 SAM 电池、AM 和 IM 的数量在计算时间方面不能很好地扩展。但是,DO 算法确实在少数情况下无法找到 SPNE。尽管如此,作者还是更喜欢 DO 算法,因为即使将问题的规模从 6 个城市增加到 55 个城市,它也不会违反单调性(收益增加)和解决方案质量趋势(计算时间非指数增加)。
3.4 研究 网络战 的论文
与网络安全不同,涉及博弈论在网络战中应用的论文很少。其中值得注意的是,Keith 等人。[84] 考虑一个多域(网络与防空相结合)防御安全博弈问题。两个玩家在零和广泛形式博弈中相互交战,一个防御者代表配备网络战保护的综合防空系统 (IADS),另一个攻击者能够释放空对地威胁(导弹、炸弹)以及网络攻击(针对 IADS 网络)。在这里,收益被选择为预期的生命损失。防御者想要最小化它,而攻击者想要最大化它。保护 IADS 的网络安全博弈问题嵌套在物理安全博弈问题中。玩家的动作对应于分配激活 IADS/网络安全响应节点对应于防御者的人口中心,以及分配给攻击者攻击 IADS/相关网络安全节点的分配。通过提供不完善的信息来增加博弈的真实性;也就是说,防御者和攻击者都没有完全意识到节点的脆弱程度。此外,防御者只能在概率上感知对节点的网络攻击,这意味着其将网络防御团队分配给特定 IADS 仅在概率上有效。对于攻击者,它还可以在物理攻击节点后确定其网络攻击的有效性。这项工作旨在通过引入集成域、代理动作的多个时期以及让玩家不断混合形式的策略来推进安全博弈文献。作者认为这是蒙特卡洛(MC)的第一部作品,并且已经在安全博弈中比较了基于折扣和稳健的反事实遗憾最小化 (CRM) 的方法。最初,对于问题的小规模版本,为防御者确定序列形式的线性规划形式的纳什均衡 (NE)。然后,这个问题逐渐扩大到包括额外的人口中心,以达到上限。在这里,引入了一种近似 CRM 算法,以减少计算时间,同时尽可能地保持特定策略的最优性。当规模进一步增加时,会引入折扣 CRM,从而进一步减少计算时间。为防御者确定序列形式的线性程序形式的纳什均衡(NE)。然后,这个问题逐渐扩大到包括额外的人口中心,以达到上限。在这里,引入了一种近似 CRM 算法,以减少计算时间,同时尽可能地保持特定策略的最优性。当规模进一步增加时,会引入折扣 CRM,从而进一步减少计算时间。为防御者确定序列形式的线性程序形式的纳什均衡(NE)。然后,这个问题逐渐扩大到包括额外的人口中心,以达到上限。在这里,引入了一种近似 CRM 算法,以减少计算时间,同时尽可能地保持特定策略的最优性。当规模进一步增加时,会引入折扣 CRM,从而进一步减少计算时间。
探索问题和算法的参数空间以选择调整参数的最佳选择并从算法中提取最佳性能。通过引入有限理性使参与者的理性受到限制,因此他们不一定做出最佳反应。他们只能管理近似稳健的最佳响应动作。玩家的稳健最佳响应定义为完全保守的 NE 策略和完全激进的最佳响应策略之间的折衷。它引入了玩家策略中的弱点。对于玩家而言,他们的策略利用对手策略的能力被称为剥削。相反,他们的策略相对于对手的脆弱性被称为可利用性。当运行所有引入的不同算法时,结果表明纳什均衡解是最安全的策略,因为正在播放的最佳动作是不可利用的,但是它不会为玩家产生最高的效用。性能图表显示,稳健的线性程序产生最高的平均效用和最高的可利用性比率,同时也消耗了最大的计算时间。数据有偏的 CFR 被认为提供了最佳的权衡,它提供了一个高平均效用、一个有利于利用的利用与利用比,同时在最短的计算时间内运行。它不会为玩家带来最高的效用。性能图表显示,稳健的线性程序产生最高的平均效用和最高的可利用性比率,同时也消耗了最大的计算时间。数据有偏的 CFR 被认为提供了最佳的权衡,它提供了一个高平均效用、一个有利于利用的利用与利用比,同时在最短的计算时间内运行。它不会为玩家带来最高的效用。性能图表显示,稳健的线性程序产生最高的平均效用和最高的可利用性比率,同时也消耗了最大的计算时间。数据有偏的 CFR 被认为提供了最佳的权衡,它提供了一个高平均效用、一个有利于利用的利用与利用比,同时在最短的计算时间内运行。
3.5 研究 太空战 的论文
Zhong等人[85] 设定了优化卫星网络带宽分配和传输功率的宏伟目标。他们的研究基于讨价还价博弈论,必须在干扰约束、服务质量要求、信道条件以及网络中每个点的卫星传输和接收能力之间达成妥协。干扰约束和带宽限制是需要在讨价还价博弈中协商的盈余,每颗卫星使用不同的策略来提高其效用/资源份额。这在复杂性上迅速升级,从模型中最重要的收获是将问题映射到合作谈判博弈框架。
同样,Qiao 和 Zhao [86] 详细介绍了卫星网络中节点的有限能量可用性的一些关键问题。他们的论文通过路由算法的博弈论模型提供了解决方案,并使用它来找到不均匀网络流量的平衡解决方案。该模型定位特定的网络热点,这些热点储备了大量的能量,并采取措施平均分配资源。这是网络中多个参与者之间的讨价还价/合作博弈的另一个案例。
3.6 与 目标跟踪 有关的论文
由于目标跟踪是一个成熟的研究领域,我们发现了几篇应用博弈论跟踪问题的论文。其中大多数具有重叠的战争领域,并没有过分强调在特定领域的适用性。例如,Gu等人[87] 研究使用传感器网络跟踪移动目标的问题,该传感器网络由能够提供一些与位置相关的目标测量的传感器组成。每个传感器节点都有一个用于观察目标的传感器和一个用于估计其状态的处理器。虽然传感器之间可以进行一些通信,但这种能力是有限的,因为每个传感器节点只能与其邻居通信。目标是一个智能代理,能够最小化对手的检测能力,从而有可能增加跟踪代理的跟踪误差,这一事实使问题更加复杂。Gu等人[87] 在零和博弈的框架内解决这个问题,并通过最小化跟踪代理的估计误差,开发了一个鲁棒的极小极大滤波器。此外,为了处理传感器节点有限的通信能力,他们提出了这种过滤器的分布式版本,每个节点只需要来自其直接邻居的当前测量和估计状态形式的信息。然后,他们在具有智能目标的模拟场景中展示了他们的算法的性能,并表明虽然标准卡尔曼滤波器误差发散,但考虑到对手噪声的极小极大滤波器可以显着优于卡尔曼滤波器。
Qilong等人[88] 类似地解决了跟踪智能目标的问题,但它们模拟了跟踪玩家也在追逐的场景,重点是保护目标。此外,目标可以向攻击者/跟踪者发射防御导弹。攻击者对目标和防御导弹都有视线。目标计划让跟踪器慢慢拉近自己与目标之间的距离,同时进行机动以了解攻击者的反应。当攻击者接近碰撞时,防御导弹被释放。然后目标和导弹进行通信,利用对攻击者运动模式的了解,并遵守最佳线性制导法则来摧毁攻击者。这被建模为攻击者、目标、和防御导弹。但是,本文也关注目标与防御导弹之间的合作博弈,这是一种非零和博弈。对他们来说,收益是通过最小化的未命中距离(理想情况下等于零——与攻击者的碰撞)以及引导防御导弹所需的控制努力来计算的。
Faruqi [89] 讨论了将微分博弈论应用于导弹制导的一般问题。他们指出,导弹轨迹遵循比例导航 (PN),这是一种通常用于制导导弹的制导法则。这些系统的性能通过线性系统二次性能指数 (LQPI) 来衡量。关于微分博弈论,他们通过用一组微分方程表示导弹导航和轨迹来模拟导弹制导问题。这个问题的一般形式是
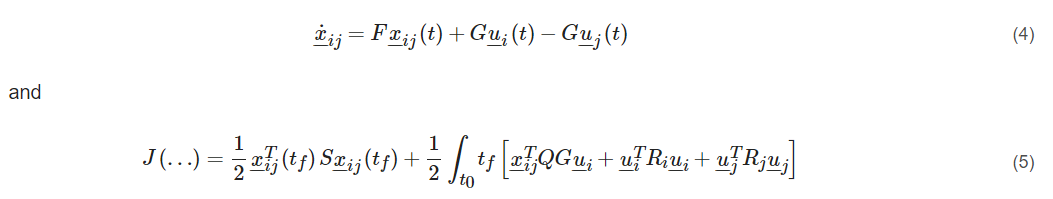
在这里,
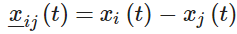
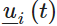
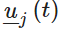
F:是状态系数矩阵
G:是玩家输入系数矩阵
Q:是当前相对状态的性能指数 (PI) 权重矩阵
S:是最终相对状态的 PI 权重矩阵
Ri,Rj:输入的 PI 权重矩阵
Faruqi 主要专注于两人和三人博弈,而效用函数是基于导弹和目标之间的相对距离向量建模的。Faruqi 表明博弈论可以有效地用于现代导弹中涉及 PN 的导弹制导任务。
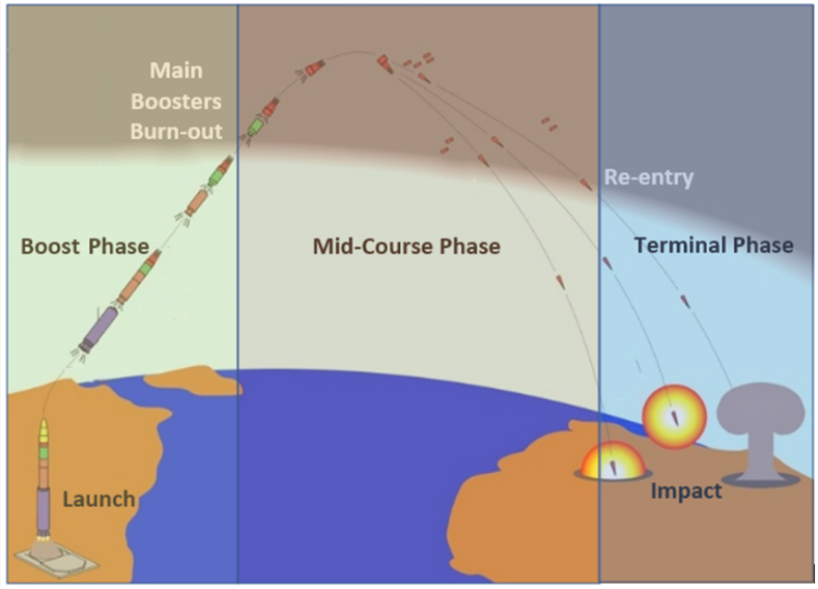
Evers [90] 另一方面,使用博弈论分析了对战区弹道导弹 (TBM) 的防御。弹道导弹和核技术的扩散对军事冲突产生了重要影响,失败的代价可能导致整个城市的毁灭。很难确定它们的发射,因为它们的射程很大,非常强大,尽管它们的有效载荷可能会有很大差异。在对抗这种威胁时,防御国确实具有通常有很长的飞行轨迹的优势,通常分为三个阶段,在此期间可以拦截 TBM。Boost 阶段标志着发射和大部分 TBM 上升。推进阶段的结束以烧毁为标志,之后 TBM 进入其中段阶段。这一阶段是飞行中最长的阶段,为防御者提供了拦截 TBM 的最佳机会。在中段阶段之后,TBM 从重新进入大气层进入其终端阶段。这是防御者拦截导弹的最后机会。飞行路线如图所示下图4。
图 4. 战区弹道导弹的飞行路径
导弹在相当长的飞行时间内飞行很长一段距离。然而,从其物理地理位置来看,一个防御的军事力量或国家只能在飞行的终止阶段运用其资源来防御它,此时风险要高得多,失败的成本也最大。出于这个原因,埃弗斯提出了一种合作战略,即防御国与周围的国家结成联盟,这样他们也可以在 TBM 到达撞击地点的早期阶段尝试拦截它。因此,博弈分为两个较小的博弈:第一个是合作多人博弈,设计一套策略供国家联盟在整个 TBM 的飞行路径中使用,第二个是防御国与潜在的盟友之间的讨价还价和合作博弈。
击落 TBM 的合作博弈的基础是一种称为“射击-观察-射击”的策略。它依赖于一组 N 个国家使用一组策略攻击目标 - 他们的拦截导弹 - M 每个国家都有自己的自己的拦截概率 Pi。当 TBM 飞行时,N 中的每个国家 n 将发射其导弹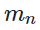
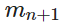
Evers描述的第二个博弈是基于与其他国家谈判结成联盟。对于这些其他国家来说,参与这场博弈是一种风险,因为这使它们成为攻击力量的另一个潜在目标。为了解决这场博弈,防御国必须准确评估拦截器成本节省,即通过阻止 TBM 的影响可以获得多少收益。随着这些储蓄成为合作国家可以分享的盈余,潜在的盟友随后就如何分享这些储蓄进行谈判,与他们必须提供的拦截资源成比例。
Shinar 和 Shima [91] 通过高度机动的弹道导弹避开拦截导弹的零和博弈,继续研究追逃博弈和弹道导弹防御。更具体地说,它将一个不完美的信息元素与博弈联系起来,弹道导弹知道它正在受到反导弹导弹的攻击,但对它们的轨迹或发射位置知之甚少。在这场比赛中,两名球员分别是弹道导弹和拦截器。如果弹道导弹使用纯粹的策略,它很可能会被击中,因为它要么 (a) 无法对它几乎没有信息的对手做出足够快的反应,要么 (b) 会以可预测的方式移动并允许直接的碰撞轨迹。因此,弹道导弹博弈的最佳解决方案是混合策略。
混合策略将在其飞行模式中加入随机性,在一组纯策略上分配概率分布。这些纯粹的策略将基于基本的导航启发式,拦截器可能知道或很容易发现。通过在策略上应用少量快速和随机的切换,弹道导弹可以最大限度地发挥其避免拦截的潜力,并将复杂的计时计算推回到拦截器上。
Bogdanovic等人[92] 使用博弈论视角研究多目标跟踪的目标选择问题。这是多功能雷达网络中的一个重要问题,因为它需要同时执行体积监视和火控等多种功能,同时有效地管理可用雷达资源以实现特定目标。因此,实际上,他们在 [92] 中解决了雷达资源管理问题,并使用非合作博弈论方法来找到该问题的最佳解决方案。他们在每个雷达都被认为是自主的框架中制定问题;没有中央控制引擎通知雷达它们的最佳策略,雷达之间也没有任何通信。首先,他们考虑了一个所有雷达对目标有共同兴趣的情况,针对这个问题,他们提出了一种基于最佳响应动力学的分布式算法来找到纳什均衡点。然后将此问题扩展到雷达和部分目标可观测性之间的异构利益的更现实的情况。对于这种情况,他们采用相关均衡的解决方案概念,并提出了一种基于遗憾匹配的高效分布式算法,该算法被证明可以实现与计算密集型集中方法相当的性能。
最后,Parras 等人[93] 研究了一种追逃博弈,涉及无人驾驶飞行器 (UAV) 的抗干扰策略。博弈在连续的时间框架内运行,因此是动态的,在微分博弈论的帮助下得到解决。在某种程度上是上述工作的高潮,它结合了通信优化、传感器规避和导航的元素。鉴于无人机需要强大的通信来控制和传递信息,这种依赖性使得无人机极易受到干扰攻击。干扰和反干扰这些通信有多种策略,这可以被认为是无人机必须尝试优化其通信能力的零和博弈。干扰代理的位置和运动通常存在不确定性,因此该博弈是一个不完全信息微分博弈。无人机最重要的回报是避免因干扰而失去通信,它可以通过机动来近似干扰代理的距离,从而避免它们。
3.7. 涉及国家安全的论文
博弈论解决的国土安全的关键组成部分是网络安全、恐怖主义威胁建模和国防合同。在计算机科学中有许多应用 [94,95,96],博弈论非常适合网络安全问题。博弈论结合了计算机科学严格的数学严谨性,以及更多的心理和哲学元素,如攻击者的动机和心态,以及人类在网络安全中的脆弱性。恐怖主义建模同样受益于博弈论的心理学风格,因为恐怖活动的许多影响不容易量化,包括受恐怖威胁影响的社会、经济和其他领域,所有这些都是在博弈论环境中建模的。最后,博弈论适用于承包和分包等主题,因为它有效地捕捉了自私个体之间的相互作用 [1,2],这已被用于模拟国防承包商的行为。
Litti [97] 的论文简要总结了如何更精确地更新传统网络安全启发式方法,以及博弈论如何帮助网络安全工程师设计策略以正确预测、缓解和处理受威胁的网络。他开发了一种定性方法来评估网络攻击的潜在风险和成本。虽然是一篇相当短的论文,但它确实提供了一些实践中博弈论的网络安全情境示例。例如,他模拟了一个两人零和博弈来代表攻击者和安全系统。节点有自己的相互依存关系、漏洞和安全资产,但要合作以最大限度地减少攻击者破坏系统的可能性。
Jhawar等人[98] 提供了一种更具体的博弈论方法,即攻击防御树 (ADT),用于对涉及网络安全威胁的场景进行建模。在这里,ADT 用于在配备自动防御协议的系统上映射潜在的攻击和防御场景。该系统需要全面解决所有可能的漏洞,并生成适应网络安全攻击不断变化的情况的响应。目前,ADT 仅提供前期系统分析。为网络安全制定反应策略很重要,因为攻击者会不断改变攻击策略,因此实时响应的时间可以决定系统防御的成功与否。在 Jhawar 等人[98] 他们模拟了一个简单的攻击者和防御者博弈——黑客和安全网络管理员。黑客试图破坏系统的完整性,并且对于他们所做的每一步,管理员都会根据攻击者的尝试设计一种反应策略。这种方法的最大效用在于能够将长而广泛的形式博弈转换为图形布局,以便于理解和交流。
Gonzalez[99] 清楚地勾勒出攻击者和防御者的标准两人竞争博弈,然后利用基于实例的学习理论和行为博弈论。前者将认知信息编译成称为实例的表示。每个实例都有一个由情境、决策和效用三部分组成的结构——一个标准的博弈。然而,实例之间的交互对这种方法至关重要。基于实例的学习理论使用从每个实例的结果中学习来反馈到下一个实例的情况,希望在以后的迭代中产生更好的决策。这与机器学习中的强化学习技术非常相似。另一方面,行为博弈论涉及设计一种策略,我们评估各种因素,对目标和资源进行更精确的长期评估,使效用分数更接近地反映现实生活价值。博弈论再次促进了网络安全应用程序中社交信息的访问,并评估了这将如何影响博弈中双方玩家的行为。其他关键因素包括玩家的动机因素、每个玩家的信息完整性以及玩家和技术之间的技术限制和低效率。Gonzalez 强调,在任何网络安全模型中考虑这些因素的重要性将有助于制定更现实和有用的网络防御政策。博弈论有助于在网络安全应用程序中访问社交信息,并评估这将如何影响博弈中两个玩家的行为。其他关键因素包括玩家的动机因素、每个玩家的信息完整性以及玩家和技术之间的技术限制和低效率。Gonzalez 强调,在任何网络安全模型中考虑这些因素的重要性将有助于制定更现实和有用的网络防御政策。博弈论有助于在网络安全应用程序中访问社交信息,并评估这将如何影响博弈中两个玩家的行为。其他关键因素包括玩家的动机因素、每个玩家的信息完整性以及玩家和技术之间的技术限制和低效率。Gonzalez 强调,在任何网络安全模型中考虑这些因素的重要性将有助于制定更现实和有用的网络防御政策。
网络安全的一种常见用途是预防恐怖主义。Hausken等人 [100] 使用一些指导性博弈论原则涵盖了恐怖主义和自然灾害建模。恐怖主义和自然灾害通过反恐、防灾和防万灾投资进行防御来解决。对这些事件中的每一个发生的可能性进行预测,防御者必须对每个防御的投资金额做出战略决策。在每种情况的效用函数中要考虑的成本包括恐怖分子的情报或自然灾害的随机性/环境控制;攻击/灾难的强度,以及恐怖分子和防御者对目标价值的评估差异。本分析中使用的博弈论方法捕捉了防御者在对抗每种威胁方面所做的努力。根据每个事件发生的可能性,结合每个防御系统的成本,防御者可以获得最佳的资金分配。
Kanturska等人[101] 对在不同位置的攻击概率未知时如何使用博弈论评估传输网络可靠性进行了严格检查。只要旅行成本相对于攻击造成的潜在损失较小,该方法就倾向于使用极小极大算法在多条路径上分配风险。这将有助于评估与安全护送贵宾通过城市相关的潜在风险。博弈论在这种情况下很有帮助,因为它可以在攻击概率未知时分析网络可靠性。
Bier[102] 为政策见解和投资决策、保单保费等提供基于博弈论的有用建议。她的工作讨论了最薄弱环节模型:一种将所有资源集中在防止最坏效用情景的策略。这在实践中通常并不理想,她建议考虑通过针对不同潜在目标的各种防御策略来对冲这些投资。该论文考虑了恐怖分子/防御者博弈,以及安全投资如何改变整个社区的攻击者与防御者互动的格局。这主要是通过它自己的范围研究来完成的,其中一个关键结论是恐怖主义缓解系统可以从博弈论中受益,因为它增加了对恐怖分子对任何防御机制的反应的额外考虑。因此,博弈论,
Cioaca [103] 调查了与 Bier 等人类似的问题。[65] 如前所述,但特别关注航空安全。通过针对机场安全措施的成本和维持稳定和有弹性的防御系统的成本来总结这个问题。关键策略是:完全防止攻击或威胁(通过删除对目标位置的所有访问权限或在航空公司未能遵守规定的指导方针时限制他们的权限);管理攻击的时间维度(攻击的长度和随后从中恢复的时间);了解所有直接和间接损失(包括人员伤亡和相关损害,如污染或感染、二级安全措施受损或声誉/信号影响);以及缓解、响应和恢复的成本。
该模型是围绕几个因素和参数建立的。首先也是最关键的是人员损失和物质损失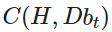
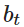
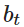
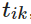
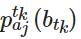
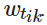
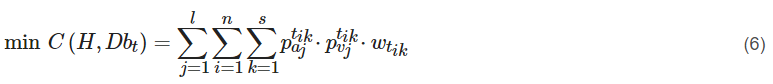
对于任何资源划分系统,Ciaoca 主张建立衡量系统弹性的维度。这分为静态弹性,资源的有效分配;动态弹性,冲击后系统的恢复速度,包括长期投资流入。这两种形式的弹性表示攻击之前、期间和之后的系统强度。在博弈论方面,Ciaoca 的研究清晰地定义了一个博弈,并结合了无数复杂且相互关联的参数,勾勒出一个有效且可计算的博弈模型。
我们讨论的关于国家安全的最后一篇论文是由 Gardener 和 Moffat [104] 撰写的。本文涵盖了制定战略以评估国防承包商及其履行合同义务的潜在绩效/能力的概念。用博弈论的说法,这个问题可以用合作和背叛来表达。加德纳和莫法特提出了量化方法,国防部可以通过这些方法更严格地评估合同和招标方案,从而明智地选择承包商并保护他们的预算。Gardener 和 Moffat 进一步了解了国防采购项目不同招标阶段项目管理的变更要求。他们关注的因素是乐观的阴谋,由于对项目进度的不合理预期,项目逐渐失控——超过了预算限制和必要的最后期限。通常,这种“阴谋”是为了获得短期收益,实际上会导致整体损失。所玩的投标博弈不再是关于项目的成功,而更多地是关于利润资本化,并可能进一步退化为相关国防部与整个承包商行业对抗的两人博弈。
3.8 研究 其他/混合战争 的论文
一些论文在防御环境中使用博弈论,但不能轻易归类为上述任何类型,或者与混合战有关。例如,Zhang和 Meherjerdi [105] 研究如何在不同的通信框架中使用博弈论方法来使用和控制多组无人驾驶车辆。将单个无人驾驶车辆的任务分配给多个无人驾驶车辆会产生更有效的任务分配和性能。将劳动力从一辆强大的单一车辆分离到几辆较小的车辆提供了灵活性、适应性和改进的容错能力。这种网络的用途是监视、探索、卫星集群、结合无人驾驶水下航行器 (UUV) 和潜艇、飞机和无人驾驶飞行器 (UAV) 以及协作机器人侦察。从这个列表中可以明显看出,该策略非常强大,因为它能够跨多个域组合资源。
同样,可以注意到,搜索是一种“捉迷藏”游戏,在军事应用中有着悠久的历史[106,107,108,109,110,111,112,113,114,115]。该理论是由 Koopman [106] 率先在军事背景下(寻找逃跑目标)提出的,随后是 Stone 等人的发展[107],应用包括潜艇狩猎、探雷、救援行动、第一响应者的风险以及危险源的定位 [106,107,108,109,110,111,112,113,114,115]。该框架提供了最优的先验给定检测模型、目标运动和搜索成本的搜索计划。搜索成本可能包括搜索时间、逃生概率(对于目标)、暴露风险(对于搜索者)、信息熵或态势感知(目标位置概率图)。搜索器可以是移动平台(UAV、UUV、巡逻艇、直升机、机器人、人),目标可以是静态的、可移动的、盲目的、无声的或发射的。在这种情况下,经常使用同时定位和映射(SLAM)算法[116]。这一利基市场的新研究方向(受一些生物学应用的启发)采用了信息趋向的思想 [117],或基于从环境中提取的信息(熵)增益(零星测量、禁区、搜索者之间的通信)实时控制搜索者的移动。博弈论的原理可以应用在可以建模为“捉迷藏”游戏的环境中。
四、分类及影响
4.1 论文分类
在上一节中,很明显,许多论文在多个领域都有适用性,并且使用了无数类型的博弈并为一系列玩家建模。因此,必须以有原则的方式对已审查的论文进行分类。为此,我们使用第 2 节表 1中已经介绍的分类方案。
特别是,可以根据 (1) 战争的领域或类型 (2) 论文中使用的一种或多种博弈类型,以及 (3) 论文中建模的玩家的性质对所审查的论文进行分类。该领域可以大致分为传统(T)或现代(M),更具体地说,可以分为陆战、海战、空战、网络战和太空战。根据博弈是非合作的还是合作的、顺序的还是同时的、离散的还是连续的、零和还是非零和,所使用的博弈类型也可以有一个复杂的分类。最后,博弈可以是两人、三人或多人(多于三人)博弈。所有这些都在表 1中进行了简要介绍。
在表 2中,我们提供了基于上述分类方案的所有评论论文的不言自明、详尽的分类。
| Title | Authors | Classification Code Using Table 1 |
|---|---|---|
| Game Theoretic analysis of adaptive radar jamming 自适应雷达干扰博弈论分析 |
Bachmann et al. | T-N-IW-NCo-Sim- -D-ZS-2P |
| Target selection for tracking in multifunction radar networks: Nash and Correlated equilibria 多功能雷达网络中跟踪目标的选择: 纳什均衡和相关均衡 |
Bogdanovic et al. | T-A-AMW-NCo- -Sim-D-ZS-NP |
| Target selection for tracking in multifunction radar networks: Nash and Correlated equilibria 雷达网络与多干扰机的功率分配博弈 |
Deligiannis et al. | T-A-IW-NCo-Sim-D-ZS-NP |
| Strategies for defending a coastline against multiple attackers 防御海岸线抵御多重攻击的策略 |
Garcia et al. | T-A-IW-NCo-Sim-C-ZS-3P |
| A game theory approach to target tracking in sensor networks 一种基于博弈论的传感器网络目标跟踪方法 |
Gu et al. | T-L-IW-NCo-Sim-D-ZS-NP |
| Joint Power allocation and beamforming between a multi-static-radar and jammer based on game theory 基于博弈论的多静雷达与干扰机联合功率分配与波束形成 |
He et al. | T-A-IW-NCo-Sim-D-ZS-2P |
| Game theoretic situation and transmission in unattended ground sensor networks: a correlated equilibrium approach 无人值守地面传感器网络的博弈情境与传输:一种相关均衡方法 |
Krishnamurthy et al. | T-L-(RAW & AMW)- -NCo-Sim-D-ZS-NP |
| Network enabled missile deflection: games and correlated equilibrium 网络使导弹偏转:博弈和相关平衡 |
Maskery et al. 2007 a | T-N-(RAW & IW) -Co-Sim-D-NZS-NP |
| Decentralised algorithms for netcentric Force Protection against anti-ship missiles 反舰导弹网络中心力量防护的分散算法 |
Maskery et al. 2007 b | T-N-(RAW & IW)- -Co-Sim-D-NZS-NP |
| Search and Screening 搜索和筛选 |
Koopman | T-(LSA)-AMW-NCo- -Slt-D-ZS-NP |
| Optimal Strategy for Target Protection with a defender in the pursuit-evasion scenario 有防御者的追逃场景下目标保护的最优策略 |
Qilong et al. | T-A-WCW- -NCo-Sim-C-ZS-3P |
| Differential game theory with applications to missiles and autonomous systems guidance 微分博弈论及其在导弹和自主系统制导中的应用 |
Faruqi | T-A-(AMW,WCW)- -NCo-Slt-C-ZS- -(2P,3P,NP) |
|
一种用于弹道导弹防御的博弈论拦截制导律 |
Shinar et al. | T-A-(AMW,WCW)- -NCo-Slt-C-ZS-2P |
| Pursuit-Evasion games: a tractable framework for anti-jamming in aerial attacks 追捕-逃避博弈:一个易于处理的框架,在空中打击抗干扰 |
Parras et al. | T-A-(WCW,IW) -NCo-Slt-C-ZS-2P |
| A simple game theoretic approach to suppression of enemy defences and other time-critical target analyses 一个简单的博弈论方法压制敌人防御和其他时间关键的目标分析 |
Hamilton et al. | T-A-(RAW,WCW)- -NCo-Slt-D-ZS-2P |
| Choosing What to Protect: Strategic Defence allocation against an unknown attacker 选择保护:针对未知攻击者的战略防御配置 |
Bier et al. | T-L-RAW-NCo- -Slt-D-ZS-2P |
| Considerations on Optimal Resource allocation in avation security 航空安全中最优资源配置问题的思考 |
Cioaca | M-C-RAW-NCo -Slt-D-ZS-2P |
| Horsemen and the empty city: A game theoretic examination of deception in Chinese military legend 骑士和空城:中国军事传说中欺骗的博弈论考察 |
Cotten et al. | T-L-RAW- -NCo-Slt-D-ZS-2P |
| An Economic Theory of Destabilisation War 不稳定战争的经济理论 |
Gries et al. | (T,M)-(IW,RAW)- -NCo-Slt-D-ZS-NP |
| Game theoretic approach towards network security: A review 网络安全的博弈论研究综述 |
Litti | M-C-IW-NCo-Slt-D-ZS-2P |
| Automating cyber defence responses using attack-defence trees and game theory 利用攻击防御树和博弈论自动化网络防御反应 |
Jhawar et al. | M-C-RAW-NCo- -Slt-D-ZS-2P |
| From individual decisions from experience to behavioural game theory 从个人决策从经验到行为博弈论 |
Gonzalez | M-C-IW-NCo- -Slt-D-ZS-2P |
| Game Theoretic Approaches to Attack Surface Shifting. Moving Target Defense II 攻击曲面移动的博弈论方法:移动目标防御II |
Manadhata | M-C-IW-NCo- -Slt-D-ZS-2P |
| Improving reliability through Multi-Path routing and Link Defence: An Application of Game Theory to Transport 通过多路径路由和链路防御提高可靠性:博弈论在交通运输中的应用 |
Kanturska et al. | M-C-RAW- -NCo-Slt-D-ZS-2P |
| Game Theoretic and Reliability’ models in counter-terrorism and security 反恐与安全中的博弈论与可靠性模型 |
Bier et al. | M-C-RAW- -NCo-Slt-D-ZS-2P |
| Changing behaviours in defence acqusition: a game theory approach 国防收购中的改变行为:一种博弈论方法 |
Gardener et al. | (T,M)- -(L,A,S,C,Sp)- -IW-NCo- -Slt-D-ZS-NP |
| Joint Transmit Power and Bandwidth Allocation for Cognitive Satellite Network based on Bargaining Game Theory 基于议价博弈的认知卫星网络联合发射功率和带宽分配 |
Zhong et al. | M-Sp-RAW-Co- -Slt-D-NZS-NP |
| The Research and Simulation of a Satellite Routing Algorithm based on Game Theory 一种基于博弈论的卫星路由算法研究与仿真 |
Qiao et al. | M-Sp-WCW- -NCo-Slt-D-ZS-NP |
| A survey of multiple unmanned vehicles formation control and coordiation. Normal and fault situations 多机器人编队控制与协调研究综述:正常和故障情况 |
Zhang et al. | T-A-WCW-Co- -Slt-D-NZS-NP |
4.2. 审查论文的影响相关指标
我们现在考虑这些论文中哪些最引起研究界的兴趣或导致后续或相关工作的问题。衡量这种影响的一个常用指标是引用计数,尽管显然这个指标偏向于早期的论文。尽管如此,在表 3中,我们展示了所考虑的 29 篇论文的 Google Scholar 引用数。哪些论文被引用次数最多,读者不言而喻,我们不再赘述。然而,我们强调,引用次数并不是衡量影响力的唯一指标,也不一定是衡量一篇论文在研究领域的影响力的最有效方法。但是,它是一种容易获得的度量,可以传达有用的信息。
| paper | 国家 | 谷歌学术 引用数 |
|---|---|---|
| Game Theoretic analysis of adaptive radar jamming 自适应雷达干扰的博弈论分析(Bachmann 等人) |
澳大利亚 | 53 |
| Target selection for tracking in multifunction radar networks: Nash and Correlated equilibria 多功能雷达网络中跟踪的目标选择:纳什和相关均衡(Bogdanovic 等人) |
荷兰 | 10 |
| Target selection for tracking in multifunction radar networks: Nash and Correlated equilibria 雷达网络和多个干扰器之间的功率分配博弈(Deligiannis 等人) |
英国 | 32 |
| Strategies for defending a coastline against multiple attackers 防御海岸线免受多个攻击者的策略(Garcia 等人) |
美国 | 7 |
| A game theory approach to target tracking in sensor networks 一种基于博弈论的传感器网络目标跟踪方法(Gu et al.) |
英国 | 72 |
| Joint Power allocation and beamforming between a multi-static-radar and jammer based on game theory 基于博弈论的多静态雷达和干扰机之间的联合功率分配和波束成形(He et al.) |
中国 | 3 |
| Game theoretic situation and transmission in unattended ground sensor networks: a correlated equilibrium approach 无人值守地面传感器网络中的博弈论情况和传输:相关平衡方法(Krishnamurthy 等人) |
美国 | 4 |
| Network enabled missile deflection: games and correlated equilibrium 网络使能导弹偏转:博弈和相关均衡 (Maskery et al. 2007 a) |
美国 | 9 |
| Decentralised algorithms for netcentric Force Protection against anti-ship missiles 针对反舰导弹的网心力量保护的分散算法(Maskery et al. 2007 b) |
美国 | 18 |
| Search and Screening 搜索和筛选 (Koopman) |
美国 | 8 |
| Optimal Strategy for Target Protection with a defender in the pursuit-evasion scenario 追逃场景中防御者目标保护的最优策略(Qilong et al.) |
中国 | 1 |
| Differential game theory with applications to missiles and autonomous systems guidance 应用于导弹和自主系统制导的微分博弈论 (Faruqi) |
澳大利亚 | 7 |
| A game theoretical interceptor guidance law for ballistic missile defence 一种用于弹道导弹防御的博弈论拦截器制导律(Shinar 等人) |
以色列 | 34 |
| Pursuit-Evasion games: a tractable framework for anti-jamming in aerial attacks Pursuit-Evasion 博弈:一种易于处理的空袭抗干扰框架(Parras 等人) |
西班牙 | 2 |
| A simple game theoretic approach to suppression of enemy defences and other time-critical target analyses 一种简单的博弈论方法来压制敌人的防御和其他时间关键的目标分析(Hamilton 等人) |
美国 | 17 |
| Choosing What to Protect: Strategic Defence allocation against an unknown attacker 选择要保护的内容:针对未知攻击者的战略防御分配(Bier 等人) |
美国 | 388 |
| Considerations on Optimal Resource allocation in avation security 航空安全中最佳资源分配的考虑 (Cioaca) |
罗马尼亚 | 3 |
| Horsemen and the empty city: A game theoretic examination of deception in Chinese military legend 骑士与空城:中国军事传奇中欺骗的博弈论检验(Cotten et al.) |
美国 | 9 |
| An Economic Theory of Destabilisation War 破坏稳定战争的经济理论(Gries 等人) |
德国 | 3 |
| Game theoretic approach towards network security: A review 网络安全的博弈论方法:综述 (Litti) |
印度 | 7 |
| Automating cyber defence responses using attack-defence trees and game theory 使用攻击防御树和博弈论自动化网络防御响应(Jhawar 等人) |
荷兰 | 3 |
| From individual decisions from experience to behavioural game theory 从经验到行为博弈论的个人决策(冈萨雷斯) |
美国 | 9 |
| Game Theoretic Approaches to Attack Surface Shifting. Moving Target Defense II 攻击面移动的博弈论方法:移动目标防御 II (Manadhata) |
美国 | 70 |
| Improving reliability through Multi-Path routing and Link Defence: An Application of Game Theory to Transport 通过多路径路由和链路防御提高可靠性:博弈论在运输中的应用(Kanturska 等人) |
英国 | 13 |
| Game Theoretic and Reliability’models in counter-terrorism and security 反恐和安全中的博弈论和可靠性模型(Bier 等人) |
美国 | 99 |
| Changing behaviours in defence acqusition: a game theory approach 在防御获取中改变行为:一种博弈论方法(Gardener 等人) |
英国 | 20 |
| Joint Transmit Power and Bandwidth Allocation for Cognitive Satellite Network based on Bargaining Game Theory 基于讨价还价博弈论的认知卫星网络联合发射功率和带宽分配(Zhong et al.) |
中国 | 13 |
| The Research and Simulation of a Satellite Routing Algorithm based on Game Theory 基于博弈论的卫星路由算法研究与仿真(Qiao等) |
中国 | 2 |
| A survey of multiple unmanned vehicles formation control and coordiation. Normal and fault situations 多辆无人驾驶车辆编队控制与协调研究:正常和故障情况 (Zhang et al.) |
加拿大 | 98 |
表 3还显示了所考虑的每篇论文的来源国,被定义为出现在通讯作者的第一个单位中的国家。可以看出,被考虑的论文是由来自美国、英国、澳大利亚、中国、荷兰、加拿大、以色列、印度、德国、西班牙和罗马尼亚的研究人员撰写的。似乎将博弈论应用于国防科学的主要兴趣存在于美国、欧洲(尤其是西欧)和中国,而我们承认可能有几篇我们没有考虑到的用英语以外的其他语言撰写的论文。
为了了解上述分类中描述的不同领域的想法是否有足够的交叉授粉,我们考虑了 29 篇审查论文中有多少论文引用了同一组中的其他论文。根据谷歌学术,引用如表 4 所示。令人惊讶的是,没有一篇论文被其他审查过的论文引用超过两次,而且大多数论文根本没有被该集中的其他论文引用。尽管该集合中论文的总体引用次数是健康的——根据表 3,审查的论文平均被引用 34.97 次,有几篇论文被引用超过 50 次。然而,这些引用大多来自与国防科学和技术有关的论文,这些论文使用各种方法和工具来解决类似的问题,很明显,在国防应用中使用博弈论的研究人员之间几乎没有交叉授粉。因此,除了我们在下面介绍的文献中的“空白”(表明潜在的研究机会)之外,还应该强调的是,应该提高对该领域类似作品的认识,这可能会导致在特定领域产生想法在与国防相关的其他领域和其他应用中被重新使用。
| paper | 国家 | 被引用 |
|---|---|---|
| Game Theoretic analysis of adaptive radar jamming 自适应雷达干扰的博弈论分析(Bachmann 等人) |
澳大利亚 | Bogdanovic et al., Deligiannis et al. |
| Target selection for tracking in multifunction radar networks: Nash and Correlated equilibria 多功能雷达网络中跟踪的目标选择:纳什和相关均衡(Bogdanovic 等人) |
荷兰 | He等人 |
| Target selection for tracking in multifunction radar networks: Nash and Correlated equilibria 雷达网络和多个干扰器之间的功率分配博弈(Deligiannis 等人) |
英国 | He等人 |
| Strategies for defending a coastline against multiple attackers 防御海岸线免受多个攻击者的策略(Garcia 等人) |
美国 |
|
| A game theory approach to target tracking in sensor networks 一种基于博弈论的传感器网络目标跟踪方法(Gu et al.) |
英国 | None |
| Joint Power allocation and beamforming between a multi-static-radar and jammer based on game theory 基于博弈论的多静态雷达和干扰机之间的联合功率分配和波束成形(He et al.) |
中国 | None |
| Game theoretic situation and transmission in unattended ground sensor networks: a correlated equilibrium approach 无人值守地面传感器网络中的博弈论情况和传输:相关平衡方法(Krishnamurthy 等人) |
美国 | None |
| Network enabled missile deflection: games and correlated equilibrium 网络使能导弹偏转:博弈和相关均衡 (Maskery et al. 2007 a) |
美国 | Bachmann et al. |
| Decentralised algorithms for netcentric Force Protection against anti-ship missiles 针对反舰导弹的网心力量保护的分散算法(Maskery et al. 2007 b) |
美国 | Bachmann et al. |
| Search and Screening 搜索和筛选 (Koopman) |
美国 | None |
| Optimal Strategy for Target Protection with a defender in the pursuit-evasion scenario 追逃场景中防御者目标保护的最优策略(Qilong et al.) |
中国 | None |
| Differential game theory with applications to missiles and autonomous systems guidance 应用于导弹和自主系统制导的微分博弈论 (Faruqi) |
澳大利亚 | None |
| A game theoretical interceptor guidance law for ballistic missile defence 一种用于弹道导弹防御的博弈论拦截器制导律(Shinar 等人) |
以色列 | Faruqi |
| Pursuit-Evasion games: a tractable framework for anti-jamming in aerial attacks Pursuit-Evasion 博弈:一种易于处理的空袭抗干扰框架(Parras 等人) |
西班牙 | None |
| A simple game theoretic approach to suppression of enemy defences and other time-critical target analyses 一种简单的博弈论方法来压制敌人的防御和其他时间关键的目标分析(Hamilton 等人) |
美国 | None |
| Choosing What to Protect: Strategic Defence allocation against an unknown attacker 选择要保护的内容:针对未知攻击者的战略防御分配(Bier 等人) |
美国 | None |
| Considerations on Optimal Resource allocation in avation security 航空安全中最佳资源分配的考虑 (Cioaca) |
罗马尼亚 | None |
| Horsemen and the empty city: A game theoretic examination of deception in Chinese military legend 骑士与空城:中国军事传奇中欺骗的博弈论检验(Cotten et al.) |
美国 | None |
| An Economic Theory of Destabilisation War 破坏稳定战争的经济理论(Gries 等人) |
德国 | None |
| Game theoretic approach towards network security: A review 网络安全的博弈论方法:综述 (Litti) |
印度 | None |
| Automating cyber defence responses using attack-defence trees and game theory 使用攻击防御树和博弈论自动化网络防御响应(Jhawar 等人) |
荷兰 | None |
| From individual decisions from experience to behavioural game theory 从经验到行为博弈论的个人决策(冈萨雷斯) |
美国 | None |
| Game Theoretic Approaches to Attack Surface Shifting. Moving Target Defense II 攻击面移动的博弈论方法:移动目标防御 II (Manadhata) |
美国 | None |
| Improving reliability through Multi-Path routing and Link Defence: An Application of Game Theory to Transport 通过多路径路由和链路防御提高可靠性:博弈论在运输中的应用(Kanturska 等人) |
英国 | None |
| Game Theoretic and Reliability’models in counter-terrorism and security 反恐和安全中的博弈论和可靠性模型(Bier 等人) |
美国 |
|
| Changing behaviours in defence acqusition: a game theory approach 在防御获取中改变行为:一种博弈论方法(Gardener 等人) |
英国 | None |
| Joint Transmit Power and Bandwidth Allocation for Cognitive Satellite Network based on Bargaining Game Theory 基于讨价还价博弈论的认知卫星网络联合发射功率和带宽分配(Zhong et al.) |
中国 | None |
| The Research and Simulation of a Satellite Routing Algorithm based on Game Theory 基于博弈论的卫星路由算法研究与仿真(Qiao等) |
中国 | None |
| A survey of multiple unmanned vehicles formation control and coordiation. Normal and fault situations 多辆无人驾驶车辆编队控制与协调研究:正常和故障情况 (Zhang et al.) |
加拿大 | None |
5. 进一步研究的机会
审查的论文表明,博弈论可以提供一个统一的框架来分析代理在防御环境中的决策行为。在本节中,我们将简要讨论迄今为止尚未应用博弈论但如果在未来应用将做出有用贡献的一系列潜在防御场景。
国防高级研究计划局 (DARPA) 最近对“马赛克战”[118] 的调查是博弈论未来潜在应用的一个例子。Zhang[105]中提到了这个想法,在操作多辆无人驾驶车辆的情况下,并建议在“马赛克”网络中互连许多具有成本效益的小型资源,这样,如果多个单元被破坏,网络的整体完整性仍然存在,就像一个即使移除了几块瓷砖,马赛克也会保留其图像。目标是,如此庞大的资源阵列具有不同的能力,将能够以其完整性和复杂性压倒敌人。它利用并发原理来解决数百万传感器和执行器系统中连接的复杂性。这些系统又必须处理系统间通信。如果成功实施,这样的系统系统可以为军事战略家提供极其强大的武器和资源网络,它可以凭借其动态的庞大规模和复杂性击败对手。这种组合武器库不同部分的方法最大限度地提高了每个部分的利益,并重新引入了对资源可消耗性的关注,而不是专注于几件高价值武器。这反过来又在策略中建立了弹性和适应性,从重量级的单一焦点攻击方法转变。由于有大量低成本资源需要合作以获得最佳结果,这种情况可以建模为一个层次的多人合作博弈,而与对手的冲突可以建模为多人非合作博弈。可以指出的是,“马赛克战争”的概念在本质上类似于更普遍的基于主体的建模概念,该概念已被用于几种不同的情况,从不老航空航天飞行器设计[119]到传染病动力学建模[120],博弈论已经成功地应用于其中一些情况[120,121]。
在海战背景下,博弈论可以有效应用的另一个领域是海军敏感性。在分析海军敏感性时,海军舰艇会考虑其环境、运动模式和潜在的对手传感器,以计算它们在秘密移动时被检测到的风险[122]。这种应用在国防科学中常用的跟踪问题之间存在重叠,正如 Gu [87] 中所解释的,它描述了使用传感器网络进行跟踪。如前所述,这种情况可以建模为两人非合作差异博弈,检测是每个玩家的主要收益参数。
事实上,基于地面的跟踪问题也可以从博弈论的应用中受益,到目前为止,该领域的论文很少。地面跟踪问题可能出现在地面军事应用(此处归类为陆战)以及国内安全和反恐应用(此处归类为国家安全应用)中,其中安全机构跟踪个人的能力'整个社会的运动——包括他们的位置、他们的社交网络和他们的动机——是一项至关重要的能力[123]。后一种情况可以建模为追求和逃避的两人博弈,或者可能只是追求和侦察,目的是不向目标透露追求,而目标会尝试识别追求。在这种情况下,从隐蔽跟踪中获得的预测信息量将是回报。
网络战建模是博弈论可以应用的另一个领域,同样,正如前面相关部分所述,除了主要来自计算机科学领域的论文之外,很少有论文涉及这一领域网络安全。金等人。[124] 描述了所有军事行动不可或缺的网络战场景,并强调了物联网 (IoT) 和脑机接口等新技术范式所发挥的关键作用。防御专家越来越需要预测和先发制敌的网络战策略。使用新颖的技术接口对涉及网络战场景的决策制定场景进行建模是博弈论可以发挥重要作用的领域。
如上所述,根据表 4 ,在所呈现的文献中,似乎很少有交叉、思想交流,甚至对其他类似作品的认识,这也可能被认为是一个“空白” 。因此,在国防应用中使用博弈论的研究人员之间加强合作是可取的,这将导致博弈论方法在多个战争领域的重用。
6. 讨论
除了总结最新技术和找出文献中的空白之外,这里还需要讨论这样的评论如何为该领域增加价值。据观察,在选定的论文集中,从一篇论文到另一篇论文的引用很少见。虽然很难确定其原因,但可以观察到,大多数研究都集中在特定的战争领域,例如陆战、海战或空战,并试图解决特定战争领域的特定问题。因此,一篇专注于不同战争领域的论文不一定被认为是另一篇将博弈论应用于国防领域的论文,而是一篇属于不同战争领域的论文,因此没有被研究。然而很明显,这种方法可能会导致错失机会,因为通常没有考虑到其他地方可以类似地应用相同的博弈论工具集。像这样的评论论文将在某种程度上纠正这个问题。此外,可以观察到,收益函数通常是根据传统上被认为是特定类型战争的重要参数的东西来严格和狭隘地定义的。例如,陆战侧重于最大限度地减少伤亡,而国家安全应用侧重于增强公众信心。然而,在大多数类型的战争中,有一系列因素促成最终的回报,从伤亡和军事资产损失到公众信心、间接经济成本、机会成本、盟友成本、以及政治和战略考虑。这篇评论论文可能会通过对多个战争领域的收益结构进行广泛概述,来激发在使用博弈论的每个战争领域中对更全面的收益函数进行建模。此外,在一般意义上,本次审查将有助于强调与国防相关的决策制定是一个有条理和理性的过程,可以进行结构化分析,而不是像过去在辩护的某些部分中所认为的那样是一个直观的过程社区 [125]。同时,所提出的分析一方面有助于避免微观管理,另一方面有助于避免冲动的决策[126],而不是鼓励国防应用中的定量决策过程。
特别是,除了运营和战术决策过程之外,所提出的审查还具有管理和社会影响。
6.1 管理影响
博弈论的应用对一个国家的国防力量非常有用,不仅在战术和作战事务方面,而且在和平时期的国防资产战略管理方面也是如此。例如,出于威慑和战备目的而对战舰、潜艇和战斗机等军事资源的战略布局,可以被视为合作博弈或等效的优化问题,可以通过线性规划或非线性规划。同样,关于战略军事设施的布局和建设的决定,例如基地、简易机场、港口,甚至公路和铁路 [127,128] 可以通过使用合作博弈论对相关场景进行建模来辅助。另一个可以应用博弈论的管理决策过程是预备役军事人员的管理,包括何时召集预备役。因此,博弈论不仅对做出作战决策的军事人员有用,而且对必须做出与国防相关的决策的文职管理人员和政治家有用,包括在和平时期,这可能会产生长期后果。
6.2 社会影响
将博弈论应用于国防场景的社会效益主要来自国家安全的观点。公众对国土安全的看法是国防考虑的重要组成部分,对国防开支有相当大的影响[129]。国防和执法部门的决策者不仅要考虑实际的风险和威胁,还要考虑感知到的风险以及受其影响的因素,例如保险成本、对旅游业的影响、信用评级机构的评级、投资者在一个国家投资的意愿、安全措施的实际成本和预期成本等,以决定国防开支。博弈论可以是一个非常有用的工具,可以对如此复杂的一组因素和参数进行建模,以及在不同场景中产生的总体收益。相反,此类决定一旦做出,显然会影响国家安全,进而影响公众对国家安全的信心和认知。因此,风险感知和国家安全支出相互影响[130,131],博弈论提供的工具集对于模拟这样一个复杂的反馈循环非常有用。显然,公众情绪和对事件的看法在战时情景中也很重要,在所有战争领域做出的决定都会影响公众的看法,这反过来又可能影响冲突的轨迹。因此,博弈论在防御场景中的应用具有明显的社会意义。
同样重要的是要注意,这篇评论增加了新的见解,有助于理解指挥和控制战。一个这样的见解是智能代理之间的合作和敌对竞争并没有乍看起来那么根本不同:事实上,从某种意义上说,它们都可以用相同的框架(博弈论)来表示,并且都涉及聪明的玩家数量、策略和收益。不同之处在于敌对竞争由非合作博弈论表示,其中一个玩家的收益增加通常会导致另一个玩家失败(零和博弈是这种情况的一个特例)。另一方面,合作以合作博弈论为代表,我们在其中模拟联盟,有时讨论“公共利益”的概念。当敌对玩家可能变成盟友或反之亦然时,这种洞察力特别有用。另一个见解是,将防御场景建模为博弈的主要困难不是来自识别可能的策略或参与者,而是来自量化收益。很多时候,我们审查过的论文在量化收益时做出了一些假设、简化和估计,并且可以设想这些过程引入的累积误差可能已经严重改变了博弈的结果,从而呈现了建模无效。因此,许多论文在应用博弈论时面临的主要挑战是准确或明智地对收益进行建模。除非对博弈论的几种防御应用进行广泛审查,否则无法获得这样的见解,
7. 结论
博弈论已被证明是一种通用且强大的工具,可用于深入了解许多领域的智能体和参与者的决策过程。在这篇评论文章中,我们详细阐述了博弈论可以应用于国防科学技术的几种场景,并简要回顾了该方向的现有研究。我们根据所研究的战争类型、使用的博弈类型和玩家的性质,对 29 篇评论论文进行了广泛的分类。基于所观察到的结果,我们发现了博弈论目前尚未得到广泛应用但在未来具有巨大应用潜力的文献中的空白;我们讨论了博弈论防御应用在未来可能扩展的潜在方向。
基于领域的分类是采用的主要分类模式,在此背景下,我们将审查的论文分为陆地、空中、海洋、网络和空间领域。我们还考虑了主要与跟踪和国家安全有关的论文。对于所考虑的每篇论文,都定义了参与者的数量和角色以及博弈类型,并在可能的情况下讨论了策略和收益函数。本练习的目的是确定最常分析的领域以及经常使用的博弈类型,并利用这些知识来确定文献中的空白,并在国防背景下跨各种领域和战争类型交叉传播想法。
希望这次审查将产生几个积极的结果。我们发现了文献中的空白,并指出博弈论提供的工具集在分析某些战争模式时并未得到充分利用。例如,我们指出,使用博弈论分析的海战论文相对较少。我们还注意到,可以通过应用博弈论来分析新兴的战争模式,例如马赛克战。因此,本次审查可能会导致更多的博弈论方法来模拟这种战争模式。此外,我们强调了该领域内的引文网络非常稀疏:也就是说,在国防应用中使用博弈论的各种研究人员之间的思想交叉授粉是很少见的。这篇综述可能会成为该领域研究人员之间合作和交叉授粉的催化剂。然而,最重要的是,这篇评论旨在向迄今为止尚未使用博弈论的国防科学家强调博弈论在国防应用中的效用,因此将为国防科学家引入一套新的工具,他们可以将其应用于他们的研究.
随着世界应对和平与稳定面临的新挑战,人类的未来取决于我们和平解决问题的能力。虽然这是一个崇高的目标,但权力的投射绝对比实际的武装冲突要好,后者在许多层面上都会付出很高的代价,博弈论确实可以在决定一些可能发生的“软冲突”中发挥作用在未来几年和几十年里。随着未来几年对国防战略和能力的关注可能会增加,博弈论可以作为一种额外的工具,国防科学家可以在许多抽象层次上使用它来解决部署、感知、跟踪和资源分配问题。
资金
专知便捷查看
便捷下载,请关注专知公众号(点击上方蓝色专知关注)
后台回复“GTDA” 就可以获取《万字长文!《博弈论在国防中的应用综述》悉尼大学与澳大利亚国防科技2022最新40页pdf综述论文》专知下载链接

请扫码加入专知人工智能群(长按二维码),或者加专知小助手微信(zhuanzhi02),加入专知主题群(请备注主题类型:AI、NLP、CV、 KG、论文等)交流~