【2022新书】熵和多样性公理化方法，452页pdf

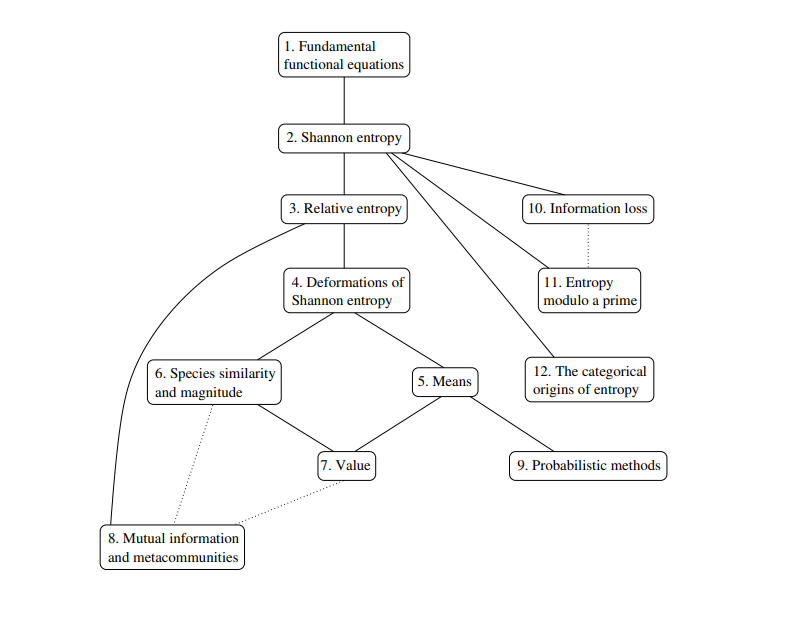
全球生物多样性危机是人类面临的最紧迫问题之一，但即使是对生物多样性进行量化也是一个数学和概念上的难题。这本书给正在进行的辩论带来了新的数学严谨性。它诞生于范畴理论的研究，通过信息论，并由古老的函数方程领域提供支持。它将公理方法的力量应用于迫切关注的生物学问题，但它也提出了独立于任何应用而独立于数学本身的新定理。“什么是多样性?”’具有惊人的数学深度，这本书涵盖了广泛的数学，从函数方程到几何测量理论，从概率论到数论。尽管范围很广，但数学先决条件很少: 本书的主要叙事线索只需要本科阶段的分析课程。

为探索衡量生物多样性的好方法带来了新的数学严谨性 假设只有适度的数学背景 展示了数学中许多明显不同的分支之间的联系 向读者介绍了一套新的数学思想和一种新的方式来理解已建立的概念熵

https://www.cambridge.org/hk/academic/subjects/mathematics/logic-categories-and-sets/entropy-and-diversity-axiomatic-approach?format=PB&isbn=9781108965576#contentsTabAnchor