【ICML2022】从block-Toeplitz矩阵到图上的微分方程:迈向可扩展掩码Transformers的一般理论

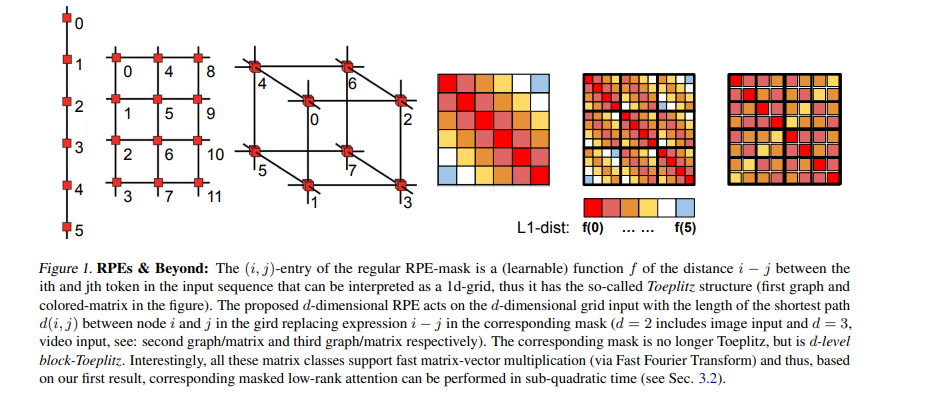
据我们所知，在本文中，我们提供了第一个全面的方法，以可扩展的方式将各种掩码机制整合到transformer架构中。我们表明，线性因果注意力(Choromanski et al.， 2021)和对数线性RPE -注意力(Luo et al.， 2021)的最新结果是这种一般机制的特殊情况。然而，通过将问题转化为未被掩盖的注意力的拓扑(基于图的)调制，我们获得了一些未知的结果，包括有效的d维RPE-掩码和图核掩码。我们利用了许多数学技术，从光谱分析、动态规划和随机漫步到解决图上马尔可夫过程的新算法。我们给出了相应的实证评价。 https://www.zhuanzhi.ai/paper/3183b33e9b7618679826d3ed338c41d8