Nature综述：金融网络中的物理学

摘要

随着全球金融市场总价值超过实体经济，金融机构构建了一个具有系统性风险的全球互动网络。理解这些网络需要新的理论方法和定量分析工具。统计物理学在此挑战中贡献显著，开发了研究金融网络结构、动力学及其稳定性与不稳定性的新度量与模型。在本综述中，作者介绍了起源于不同金融关系的网络表征方法，包括直接交互（如贷款）、相似关系（如共持股）以及更高阶关系（如涉及多方的信用违约互换 (credit default swaps)）或多层连接（可能扩展到实体经济）。随后，回顾了捕捉冲击在各系统中传播及影响的金融传染（financial contagion）模型。最后，讨论了经济学与统计物理学中不同的“平衡”概念，以及它们如何导出图的最大熵集，并为金融网络推断和全局不稳定性早期预警信号识别提供工具。

**

**

**关键词：金融网络，统计物理，金融传染，系统性风险 ，最大熵 ，多层网络 **********************************

彭晨丨作者

论文题目：The physics of financial networks 论文链接：https://www.nature.com/articles/s42254-021-00322-5 发表时间：2021年6月10日 论文来源：Nature Reviews Physics **

**

网络结构的多样化表征

在金融全球化与资产价值持续膨胀的背景中，将金融系统建模为网络已成为揭示其内在复杂性交互与系统性风险的核心视角。通过将银行、保险公司、投资基金、企业甚至家庭等经济主体视为网络节点（nodes），并用代表贷款、股权、担保等合同关系的边（edges）连接它们，研究者得以直观地描述金融系统的微观结构与宏观风险特征。 最简单的单层网络 (single-layer networks) 聚焦于两类基本关系：一类是所有权网络 (ownership networks)，体现了通过股权链条传递的控制与影响；另一类是信贷网络 (credit networks)，展现了银行之间借贷的风险互联 。 然而，金融主体往往同时存在多种关系，因而更真实的表征是多层网络 (multiplex networks)：同一节点在不同层上通过不同类型的边连接，其结构可以随时间演化。更高级的模型则引入高阶交互 (higher-order interactions)，如多方参与的衍生品合约，使网络表征超越二元连接，捕捉更丰富的风险传导机制。

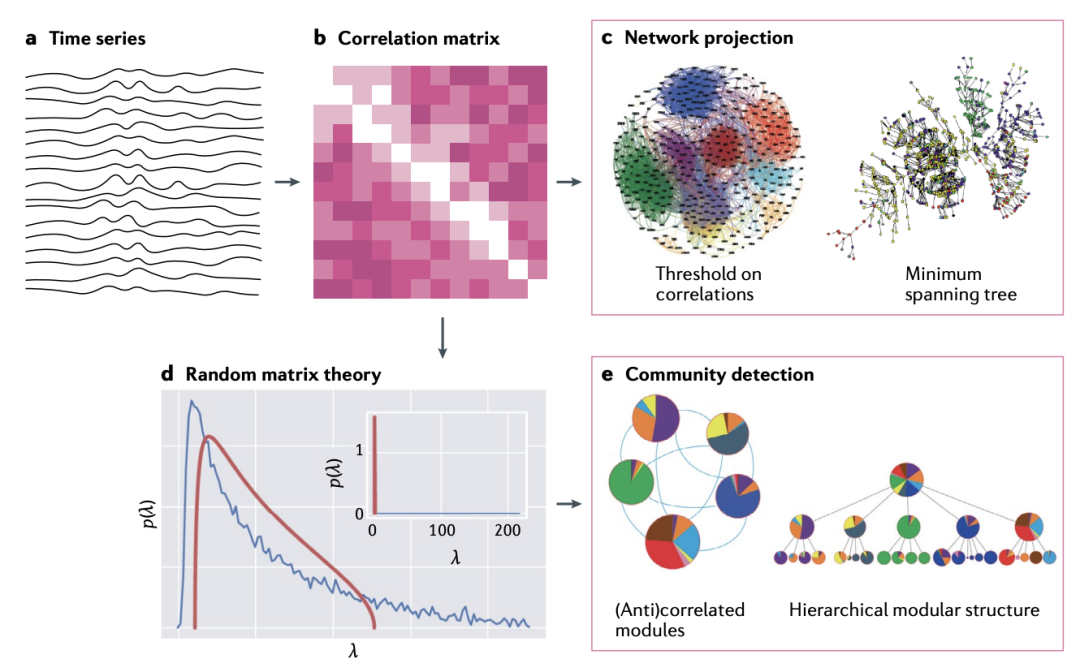
图 1. 基于多元时间序列的相关性网络。a：原始数据由 n 个时间序列组成，每个序列跨越 m 个时间步。b：数据被转换为一个 n×n 的相关矩阵 C，其中的元素cij是第 i 个和第 j 个时间序列之间的相关系数。c-e：可以利用相关矩阵 C 从原始的 n 个对象中生成不同类型的网络结构，要么直接创建一个由相关系数cij超过给定阈值的节点对连接而成的网络（部分 c），要么将其归入某种嵌入几何结构（如最小生成树或最大平面图）（部分 c），要么通过将 C 的特征值的经验分布（蓝色线）与随机相关矩阵（随机矩阵理论中的 Wishart 集合）所呈现的预期的 Marchenko-Pastur 密度（红色线）进行比较来过滤掉噪声和全局成分，随后识别出内部相关性最大且相互间相关性最小的时间序列社区（部分 e）。部分 c 和 e 中的网络是通过这种方式获得的。从标准普尔 500 市场的股票时间序列出发，不同颜色代表股票所属的不同板块：在所有情况下，板块并不能预测网络结构，这表明网络结构编码了高于标准分类的高阶信息。

**

**

金融传染：直接与间接

金融传染的核心在于，当单个主体因资产价值骤降或负债层级触及违约临界时，如何通过网络结构将冲击扩散至其他主体。直接传染机制主要包括偿付能力传染 (solvency contagion) 与流动性传染 (liquidity contagion)。在偿付传染中，当银行A因资产减值导致自身资产枯竭，其债权人在对其资产进行重估后也可能陷入资不抵债，从而触发连锁违约。这一过程可用“债权人—债务人”双向加权网络加以模拟，其代表性模型为Eisenberg-Noe框架，通过迭代算法计算部分支付与违约损失在网络中的传染路径 。 流动性传染则关注短期负债与可变现资产的动态匹配：当主体无法通过现金或高流动性资产满足到期债务时，被迫抛售持有资产以补充流动性。快速抛售造成价格下跌，进一步加剧其他同质资产持有者的损失，并可能在网络中形成雪崩式的冲击放大效应。 除直接合同关系外，主体还可能因共同持有同一类资产而相互关联，形成**重叠投资组合 **(overlapping portfolios) 网络。这一网络是典型的二分网络 (bipartite networks)，一类节点为金融机构，另一类为资产。当某机构因风险管理或杠杆要求被迫抛售资产时，资产价格下跌会给所有持有相同资产的机构带来损失，并可能引发进一步抛售。研究者通常利用市场冲击函数和线性阈值模型刻画此类动态，发现投资多样化虽能降低个体风险，却不一定提高系统整体稳定性；在某些参数区间，过度多样化反而加剧系统脆弱性，呈现典型的“鲁棒却脆弱”（robust-yet-fragile）特征。

**

**

多层网络与混合传播

真实金融系统中，不同传染渠道并行存在：合同违约、融资撤回、资产抛售等渠道各自构成网络层，且层间风险可能相互叠加或抵消。将多层网络与多渠道传染模型结合，能够更全面评估系统性风险。研究表明，弱耦合的多层网络相比单层网络风险更为集中，且在临界点处常伴随更陡峭的相变；而不同层风险的非线性交互可能使单层视角严重低估整体风险，可多达 90% 的系统风险在单层模型中被忽略 。

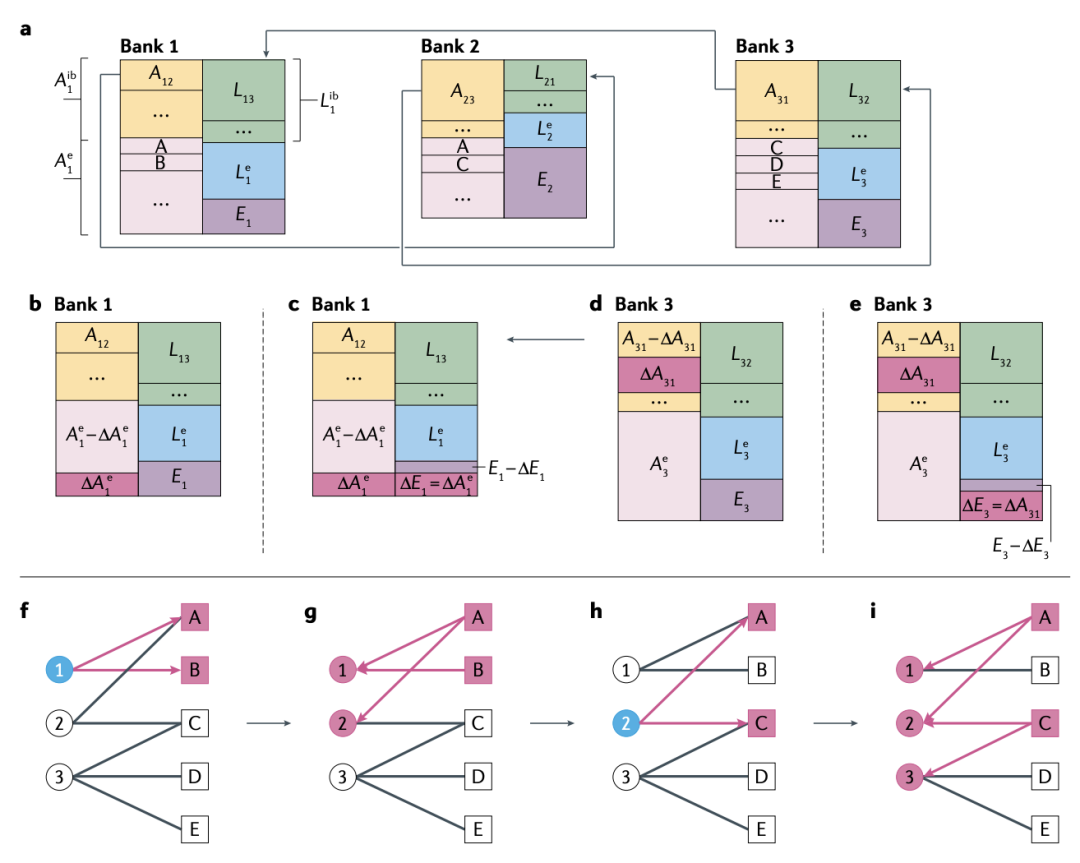
图 2. 银行间网络及其动态。一个由三家银行组成的程式化银行间网络，每家银行都用其资产负债表表示。资产方面是银行间资产，进一步分解为单个风险敞口，以及外部资产a。负债方面是银行间负债，同样被分解为外部负债和股权负债。b-e：通过银行间资产重估的偿付能力传染。外生冲击冲击银行1的外部资产（b部分），并被银行1的权益（c部分）吸收。由于银行3对银行1有风险敞口，它重新评估其银行间资产（part d）。具体的估值方法取决于具体的模型。最后，银行3的资产减少被其股本所吸收（第e部分）。f-i：重叠投资组合的传染。例如，银行1出售资产A和资产B，以实现其杠杆目标（第f部分）。这样做会导致A和B贬值。持有A和B的银行1和银行2的资产价值减少（第g部分）。因此，银行2现在需要去杠杆化并出售资产a和C（h部分）。这些资产折旧和银行1、2和3的资产价值减少（i部分）。

**

**

统计物理视角下的金融网络

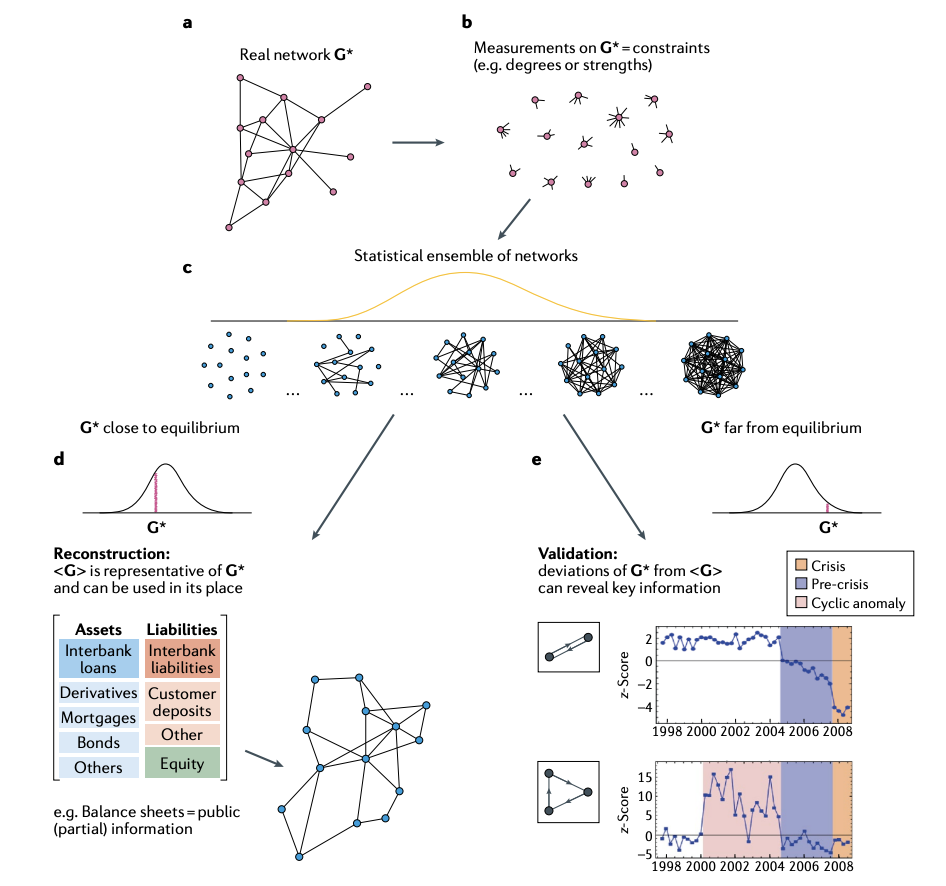
面对金融网络高维、缺失数据与保密限制，统计物理学提供了**最大熵网络集成 **(maximum entropy ensembles) 的方法论：在只知节点度（degree）或节点强度（strength）等局部约束的情况下，通过最大化香农熵构造图谱的概率分布，既可作为缺失数据条件下的“最佳猜测”进行网络重构 (network reconstruction)，也可作为已观测网络的平衡态 (equilibrium) 基准，识别异常亚结构作为危机前兆 。例如，对荷兰银行业网络中二元与三元环的统计显著性变化能够早于2008年危机发生而给出预警。此外，将经济学中的瓦尔拉斯均衡 (Walrasian equilibrium)与热力学平衡相结合，进一步揭示如果真实网络确实源于市场均衡，则在相同供需约束下所允许的所有配置应同属热力学平衡态，从而为理论与实证研究提供统一视角。

图 3. 金融网络统计集合的构建及其在网络重构和模式检测中的应用。从现实世界的网络G* （图a）开始，选择结构属性的集合C(G*)作为约束——例如，所有节点的度和/或强度（图b）。然后，通过计算在选定的约束条件下使香农熵最大化的概率分布P(G|θ)和使似然最大化的参数θ*，构造一个典型网络集合（图c）。这种构造保证了约束的期望值与经验值相匹配。如果C(G*)是关于原始网络G的唯一可用信息，并且后者被认为处于由所选约束引起的热力学平衡状态，则集合可以用作网络重建的方法。或者，集合作为零模型来检测G与平衡的经验偏差，例如，小子图（二组或三组）发生的系统变化，甚至可能作为网络结构重大转变的预警信号（图e）。在所示的例子中，荷兰银行间网络中2阶和3阶周期的统计显著性变化被证明是2008年危机的预警信号。

结语

综上所述，统计物理学在金融网络研究中扮演了桥梁角色，不仅为理解复杂网络结构、风险扩散机制与系统稳定性提供了新范式，也为政策制定者和监管机构提供了定量工具。未来，随着多源异构数据的获取与高性能计算的发展，多层次、多尺度的网络模型有望进一步提升金融系统的可解释性与预测能力，为防范系统性风险与维护金融稳定贡献更大力量。

---