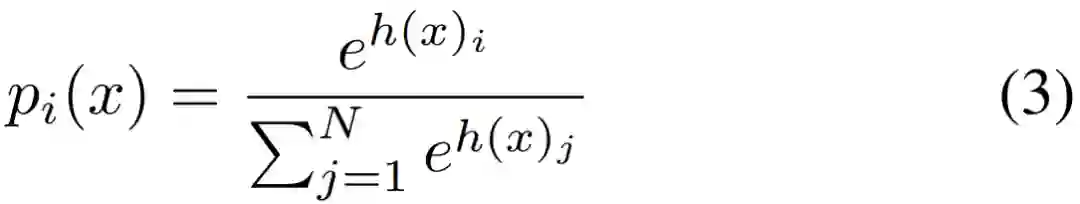来自 Meta AI 和纽约州立大学布法罗分校的研究者分析了 MLP 在表达能力方面的局限性,并提出了在特征和输入(token)维度上带有混合专家系统(MoE)的稀疏激活 MLP。
作为基于注意力模型的替代方案,纯 MLP 架构吸引了越来越多的关注。在 NLP 中,gMLP 等近期工作表明,纯 MLP 在语言建模方面可以达到与 transformer 相当的性能,但在下游任务中弱于 transformer。
来自 Meta AI 和纽约州立大学布法罗分校的研究者分析了 MLP 在表达能力方面的局限性,并提出了在特征和输入(token)维度上带有混合专家系统(MoE)的稀疏激活 MLP。这种稀疏的纯 MLP 显著提高了模型容量和表达能力,同时保持计算不变。该研究解决了将条件计算与两种路由策略结合起来的关键挑战。
![]()
论文地址:https://arxiv.org/pdf/2203.06850.pdf
与基于 transformer 的 MoE、密集 Transformer 和纯 MLP 相比,该研究提出的稀疏纯 MLP(sMLP) 改进了语言建模的困惑度并获得了高达 2 倍的训练效率提升。最后,研究者在六个下游任务上评估了稀疏纯 MLP 的零样本上下文学习性能,发现它超过了基于 transformer 的 MoE 和密集的 transformer。
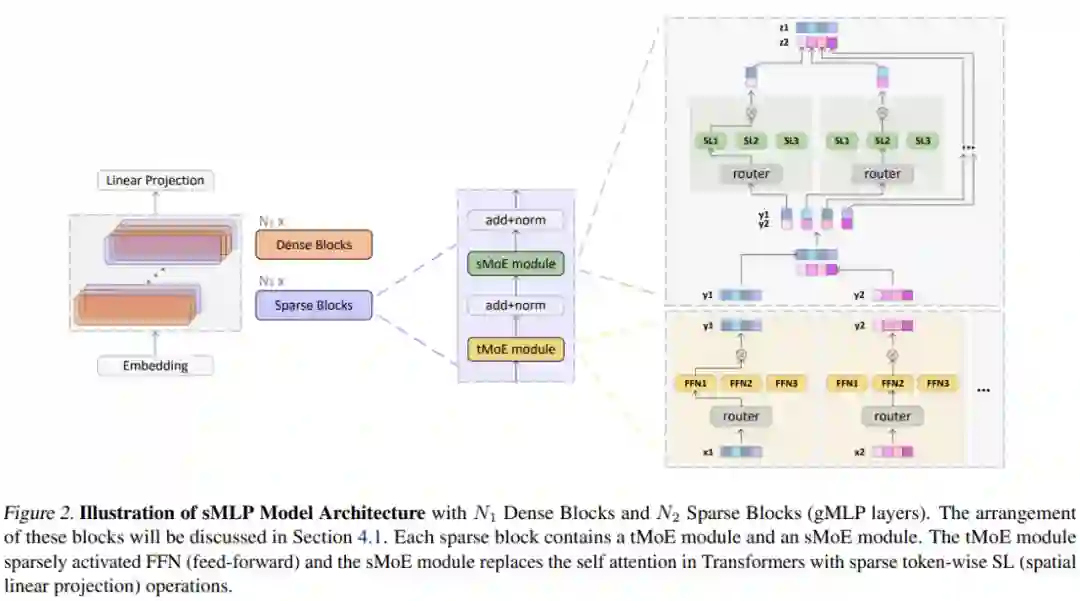
sMLP 的整体架构如下图 2 所示,包含 N_1 个密集块和 N_2 个稀疏块。N_1 和 N_2 都是超参数。每个稀疏块包含两个模块:
tMoE 模块:该研究采用 Base Layers 的 MoE (Lewis et al., 2021) 来替换密集 transformer 中的 FFN 模块 (Vaswani et al., 2017b);
sMoE 模块:该研究设计了 sMoE 模块来替代 transformer 中的自注意力模块(Vaswani et al., 2017b)和 gMLP 中的空间门控单元(SGU,Liu et al., 2021a)。
![]()
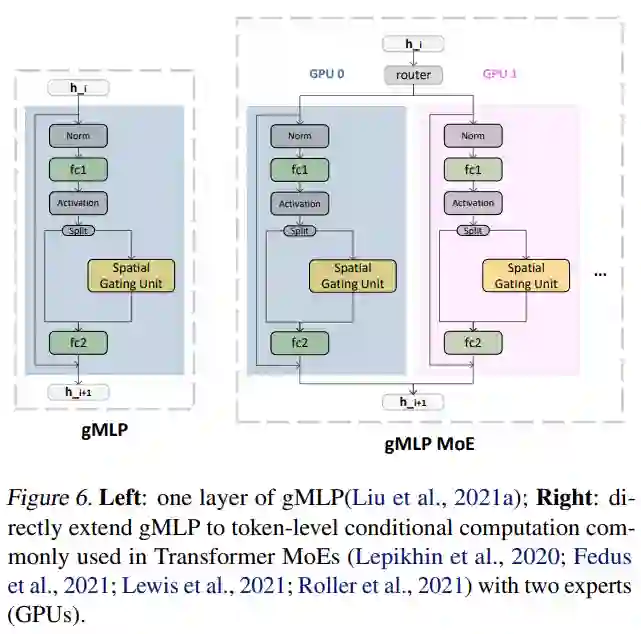
专家模块负责处理输入。对于 tMoE 模块,每个专家都包含一个 FFN,如上图 2 所示。对于 sMoE 模块,每个专家都包含空间门控单元,如下图 6(右)所示。
![]()
该模块决定哪个专家应该处理输入的每个部分,因此需要设计一种独特的路由方法来将 MoE 结构扩展到特征维度。
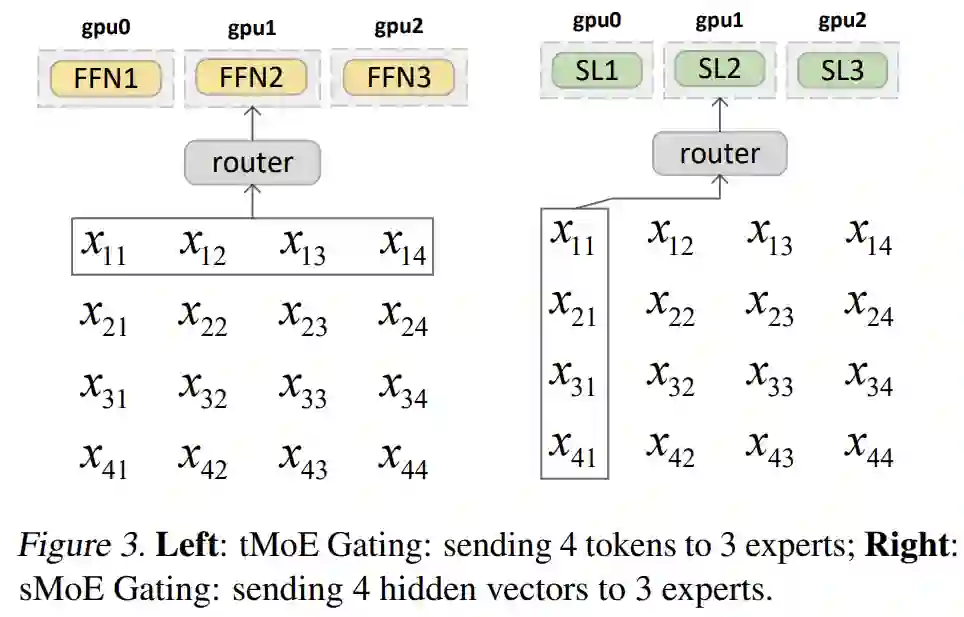
图 3(左)显示了现有基于 transformer 的 MoE 的门控函数示例(Lepikhin et al., 2020;Fedus et al., 2021;Lewis et al., 2021;Roller et al., 2021)。x_ij 表示 i_th token 中 j_th 隐藏维度的值。
![]()
![]()
tMoE 使用由
![]() 参数化的
等式(3)中描述的学习门控函数将这 4 个 token 发送给 FFN 层的 3 个专家。
与已有的一些 MoE 不同,在稀疏纯 MLP 架构中,该研究提出沿隐藏维度对隐藏表示进行分块,并将分块向量发送给不同的专家,如图 3(右)所示。
与这些现有的 MoE 不同,在稀疏的全 MLP 架构中,该研究提出沿隐藏维度对隐藏表示进行分块,并将分块向量发送给不同的专家,如图 3(右)所示。
与路由 token 相比,路由隐藏维度在自回归模型中面临着一个独特的挑战,如果简单地预测未来的 token,信息会泄漏。此外,与具有 selfattention 的基于 Transformers 的 MoE 不同,此处不能直接应用适当的掩码来防止信息泄露,因此不能在基于 transformer 的 MoE 中采用现有的路由方法进行语言建模。该研究比较了以下两种解决方案:确定性路由(deterministic routing)和部分预测(partial prediction)。
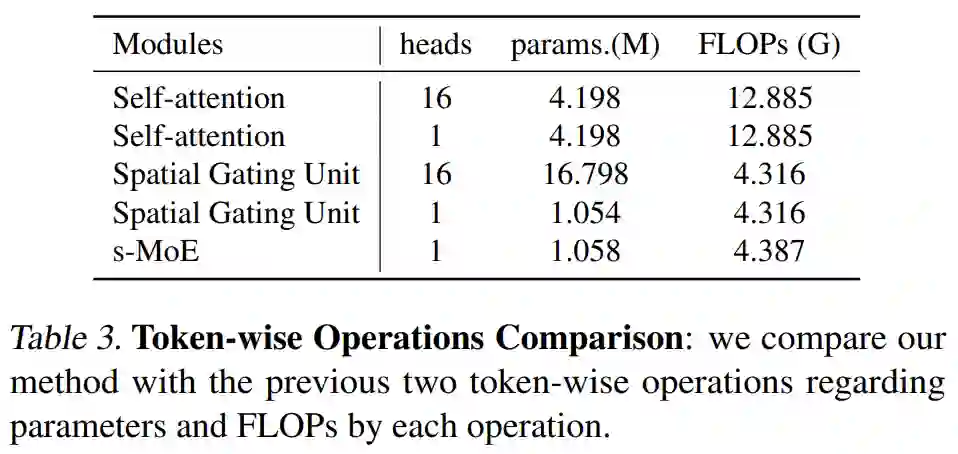
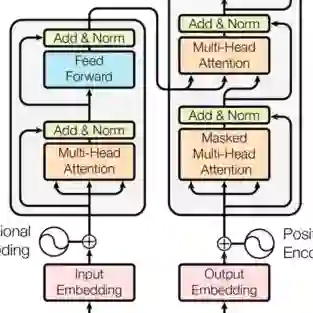
该研究将 sMLP 模型与两个密集模型进行比较:Transformer (Vaswani et al., 2017b) 和 gMLP (Liu et al., 2021a)。基于全 MLP 和基于 transformer 的模型之间的主要区别在于 token 操作。该研究比较了这三种 token-wise 操作:Transformers 中的 self-attention 模块、gMLP 中的 Spatial Gating Unit 和 sMLP 模型中的 sMoE 模块。表 3 比较了三种 token 操作及其各自的头部机制:
参数化的
等式(3)中描述的学习门控函数将这 4 个 token 发送给 FFN 层的 3 个专家。
与已有的一些 MoE 不同,在稀疏纯 MLP 架构中,该研究提出沿隐藏维度对隐藏表示进行分块,并将分块向量发送给不同的专家,如图 3(右)所示。
与这些现有的 MoE 不同,在稀疏的全 MLP 架构中,该研究提出沿隐藏维度对隐藏表示进行分块,并将分块向量发送给不同的专家,如图 3(右)所示。
与路由 token 相比,路由隐藏维度在自回归模型中面临着一个独特的挑战,如果简单地预测未来的 token,信息会泄漏。此外,与具有 selfattention 的基于 Transformers 的 MoE 不同,此处不能直接应用适当的掩码来防止信息泄露,因此不能在基于 transformer 的 MoE 中采用现有的路由方法进行语言建模。该研究比较了以下两种解决方案:确定性路由(deterministic routing)和部分预测(partial prediction)。
该研究将 sMLP 模型与两个密集模型进行比较:Transformer (Vaswani et al., 2017b) 和 gMLP (Liu et al., 2021a)。基于全 MLP 和基于 transformer 的模型之间的主要区别在于 token 操作。该研究比较了这三种 token-wise 操作:Transformers 中的 self-attention 模块、gMLP 中的 Spatial Gating Unit 和 sMLP 模型中的 sMoE 模块。表 3 比较了三种 token 操作及其各自的头部机制:
![]()
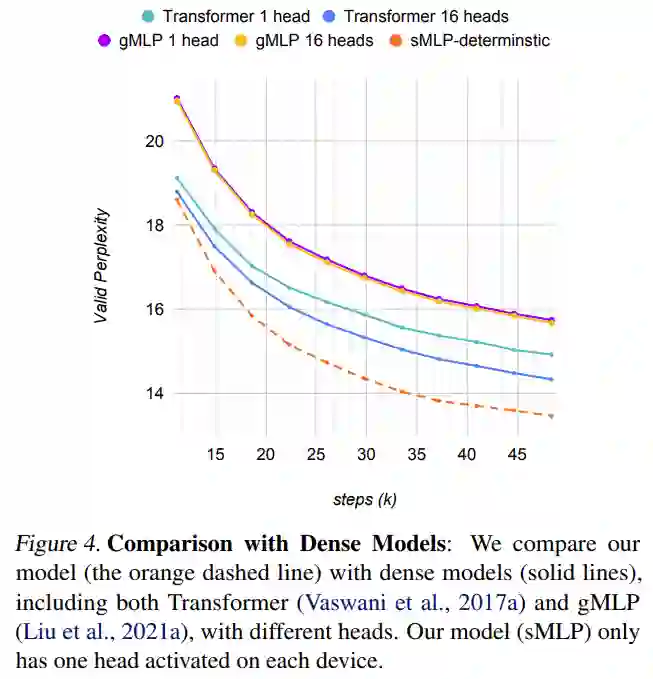
下图 4 将模型与不同头数的密集模型进行了比较。Transformer 模型极大地受益于多头机制。然而,gMLP 模型虽然增加了参数量,但并没有通过多头机制提高性能。sMLP 模型也可以看作是 gMLP 的一种多头解决方案,显著提高了基于 MLP 模型的性能,并且优于 transformer 模型。
![]()
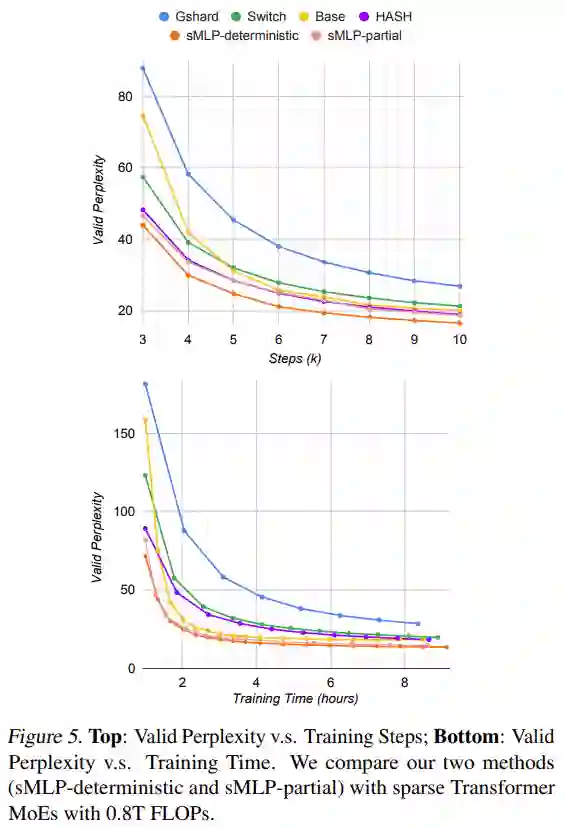
下图 5 给出了质量(有效困惑度)和训练效率,通过训练步骤数(顶部)和训练时间(底部)来衡量。研究者发现,具有两种路由策略变体的 sMLP 优于具有大致相同数量的 FLOP 的最先进的基于 Transformer 的 MoE 模型。
![]()
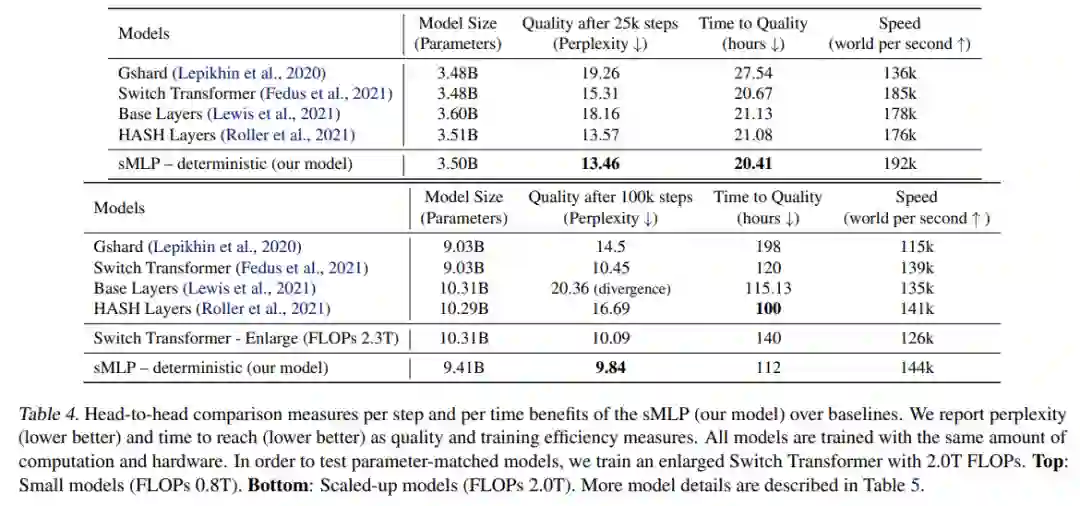
下表 4 总结了主要实验中的详细比较结果。研究者将所有模型的 FLOPs 控制为约 0.8T。除了模型层数不同,它们的嵌入维数为 1024,隐藏维数为 4096。可以看到,sMLP 模型在 25k 训练步骤时实现了最好的泛化,同时实现了最高的训练速度。HASH 层在所有 Transformer 基线中具有最佳性能,并且需要的时间最少。
![]()
![]()
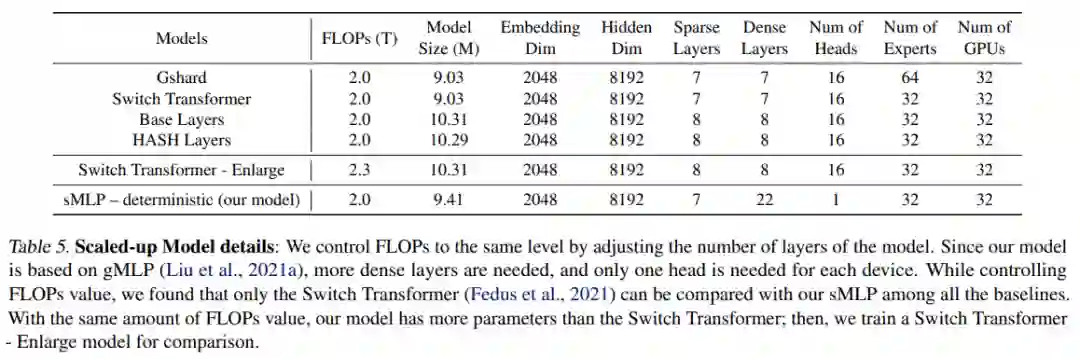
为了测试模型的可扩展性,该研究增加了 2.0 TFLOPs 的模型大小训练。表 4(底部)总结了结果。
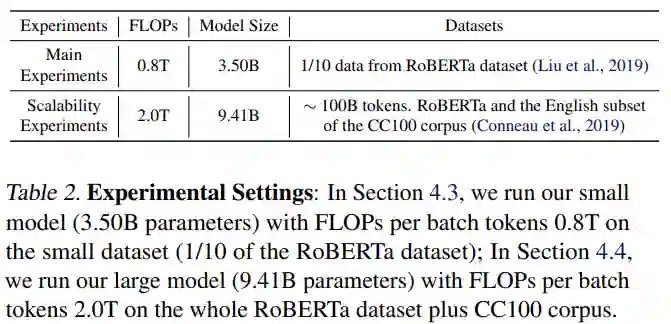
与表 4(顶部)中的模型相比,该研究扩大了所有模型,将嵌入从 1024 更改为 2048,并将隐藏维度从 4096 调整为 8192,如表 5 所示。该研究还增加了预训练数据大小,如表 2 所示。
![]()
IJCAI 2022 - Neural MMO 海量 AI 团队生存挑战赛
4月14日,由超参数科技发起,联合学界MIT、清华大学深圳国际研究生院以及知名数据科学挑战平台 AIcrowd 共同主办的「IJCAI 2022-Neural MMO 海量 AI 团队生存挑战赛」正式启动。
本届赛事以「寻找未来开放大世界的最强 AI 团队」为主题,通过在 Neural MMO 的大规模多智能体环境中探索、搜寻和战斗,获得比其他参赛者更高的成就。比赛还设置新的规则,评估智能体面对新地图和不同对手的策略鲁棒性,在 AI 团队中引入合作和角色分工,丰富了比赛内容,增强了趣味性。
比赛设立了
20000美元的奖金池
以及丰富的
学术荣誉奖 & 趣味奖
,比如“酸脚(Jio)奖”。对比赛感兴趣的小伙伴点击阅读原文赶紧报名吧!
![]()
© THE END
转载请联系本公众号获得授权
投稿或寻求报道:content@jiqizhixin.com
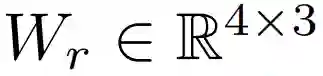 参数化的
等式(3)中描述的学习门控函数将这 4 个 token 发送给 FFN 层的 3 个专家。
与已有的一些 MoE 不同,在稀疏纯 MLP 架构中,该研究提出沿隐藏维度对隐藏表示进行分块,并将分块向量发送给不同的专家,如图 3(右)所示。
参数化的
等式(3)中描述的学习门控函数将这 4 个 token 发送给 FFN 层的 3 个专家。
与已有的一些 MoE 不同,在稀疏纯 MLP 架构中,该研究提出沿隐藏维度对隐藏表示进行分块,并将分块向量发送给不同的专家,如图 3(右)所示。