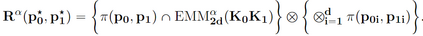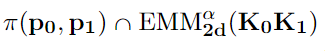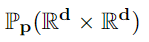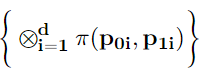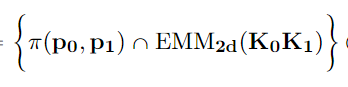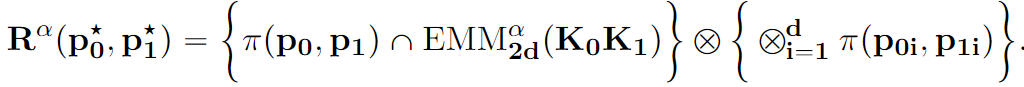Robust probabilistic inference via a constrained transport metric

Flexible Bayesian models are typically constructed using limits of large parametric models with a multitude of parameters that are often uninterpretable. In this article, we offer a novel alternative by constructing an exponentially tilted empirical likelihood carefully designed to concentrate near a parametric family of distributions of choice with respect to a novel variant of the Wasserstein metric, which is then combined with a prior distribution on model parameters to obtain a robustified posterior. The proposed approach finds applications in a wide variety of robust inference problems, where we intend to perform inference on the parameters associated with the centering distribution in presence of outliers. Our proposed transport metric enjoys great computational simplicity, exploiting the Sinkhorn regularization for discrete optimal transport problems, and being inherently parallelizable. We demonstrate superior performance of our methodology when compared against state-of-the-art robust Bayesian inference methods. We also demonstrate equivalence of our approach with a nonparametric Bayesian formulation under a suitable asymptotic framework, testifying to its flexibility. The constrained entropy maximization that sits at the heart of our likelihood formulation finds its utility beyond robust Bayesian inference; an illustration is provided in a trustworthy machine learning application.