Physics Informed Neural Networks for Modeling of 3D Flow-Thermal Problems with Sparse Domain Data

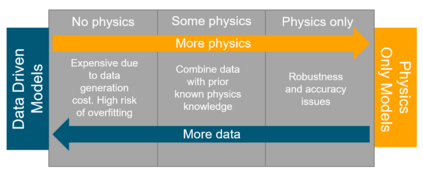
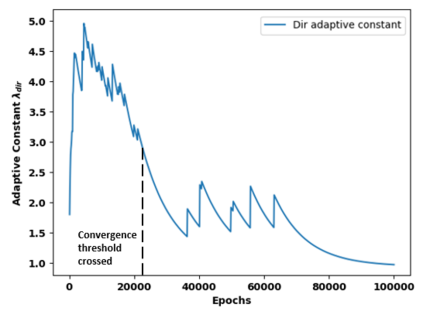
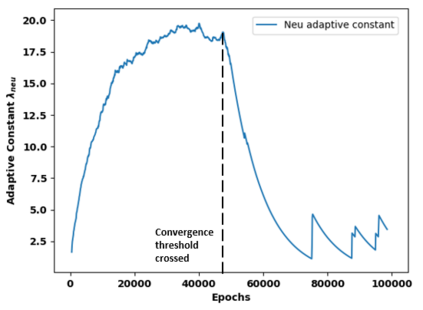
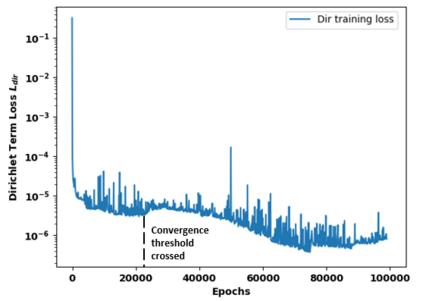
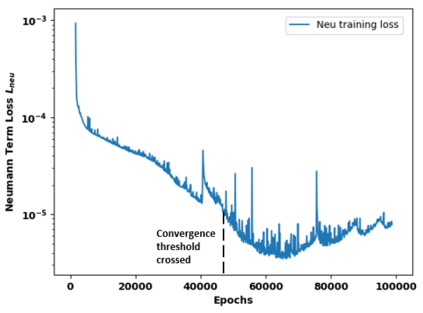
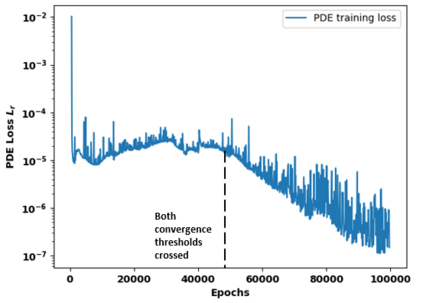
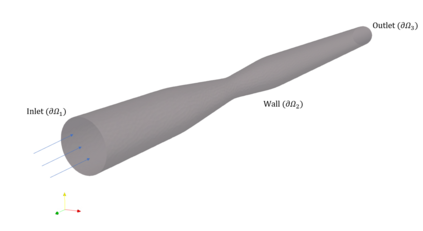
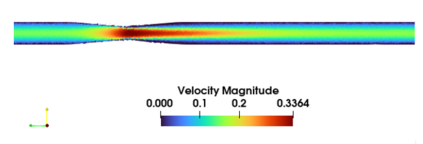
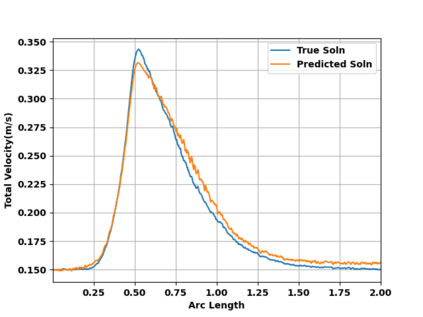
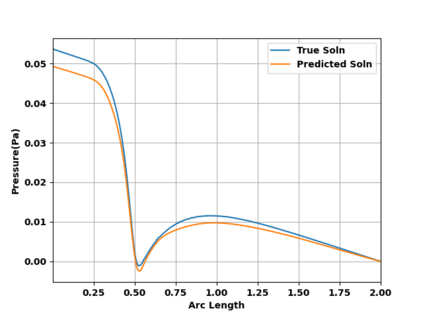
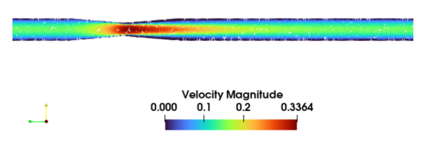
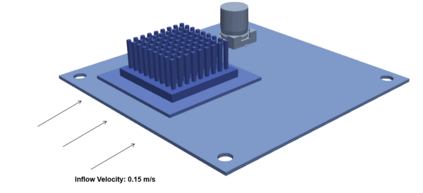
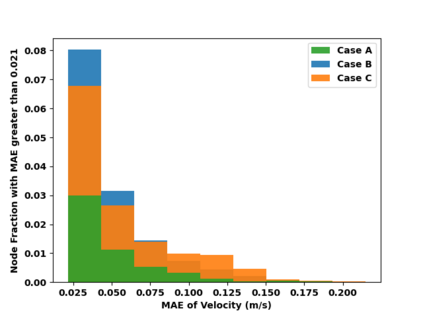
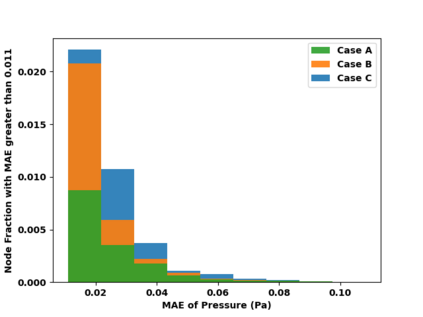
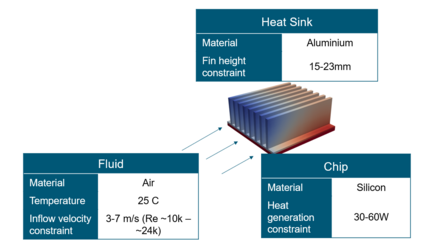
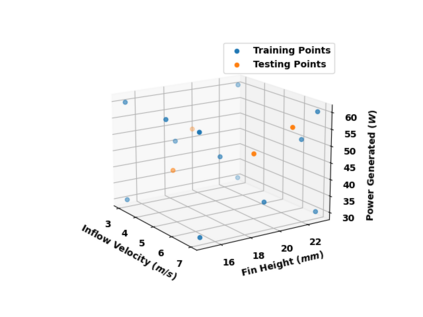
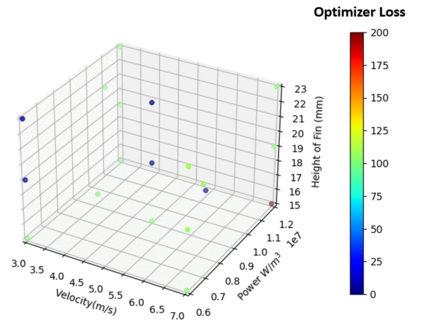
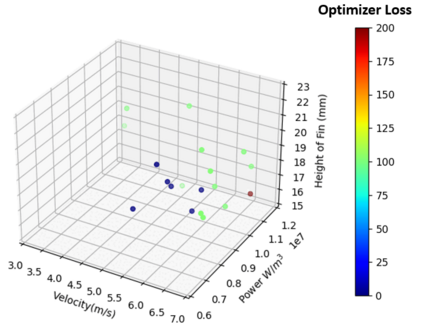
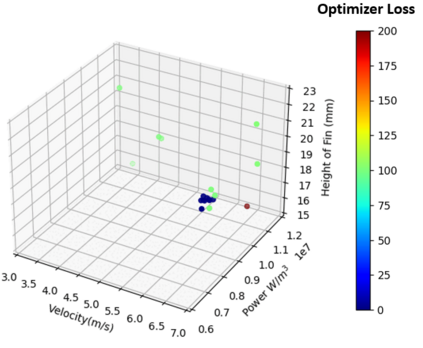
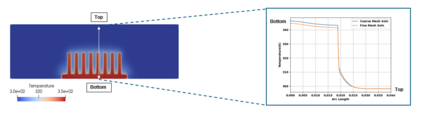
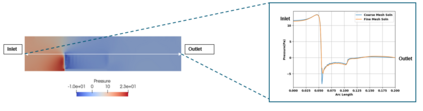
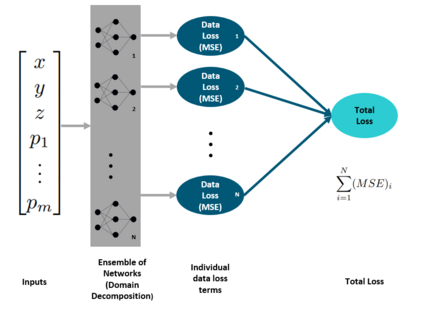
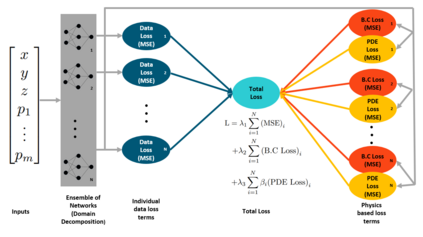
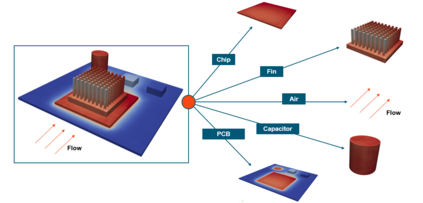
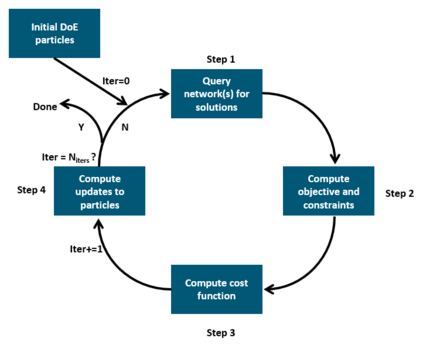
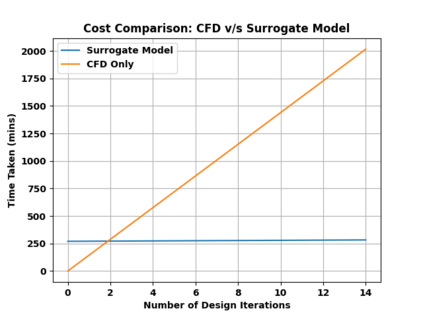
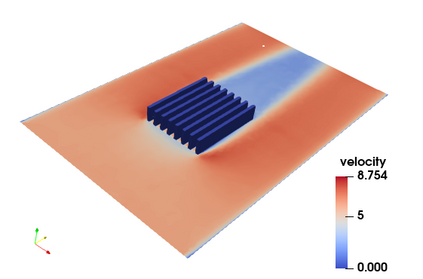
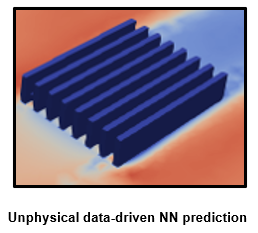
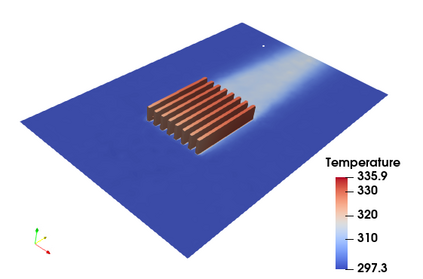
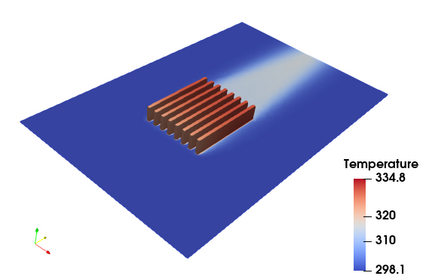
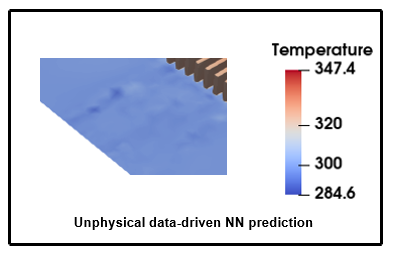
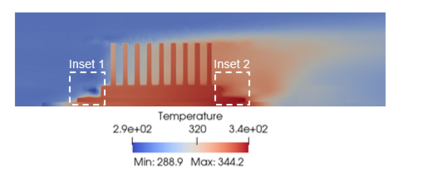
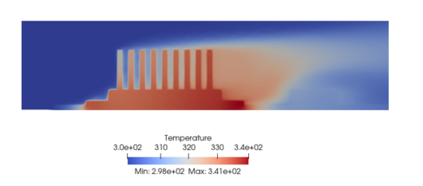
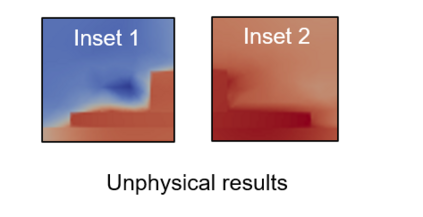
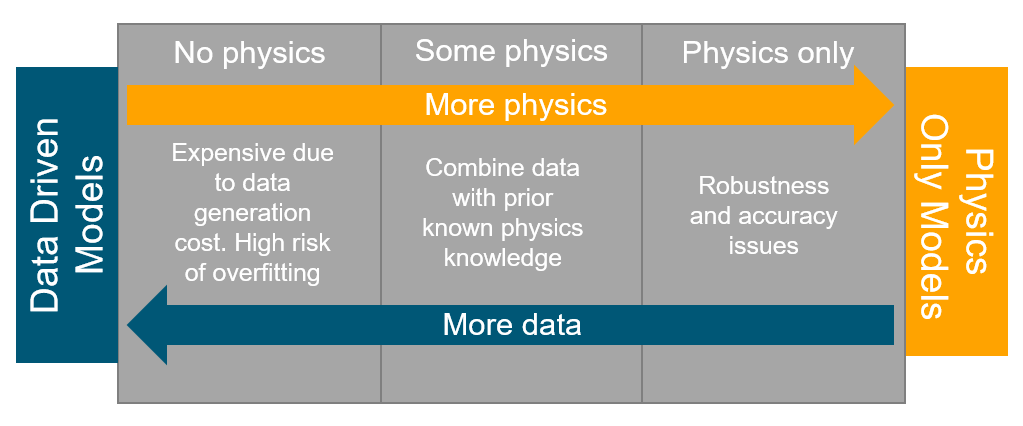
Successfully training Physics Informed Neural Networks (PINNs) for highly nonlinear PDEs on complex 3D domains remains a challenging task. In this paper, PINNs are employed to solve the 3D incompressible Navier-Stokes (NS) equations at moderate to high Reynolds numbers for complex geometries. The presented method utilizes very sparsely distributed solution data in the domain. A detailed investigation on the effect of the amount of supplied data and the PDE-based regularizers is presented. Additionally, a hybrid data-PINNs approach is used to generate a surrogate model of a realistic flow-thermal electronics design problem. This surrogate model provides near real-time sampling and was found to outperform standard data-driven neural networks when tested on unseen query points. The findings of the paper show how PINNs can be effective when used in conjunction with sparse data for solving 3D nonlinear PDEs or for surrogate modeling of design spaces governed by them.