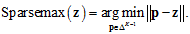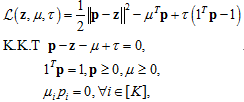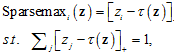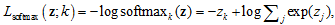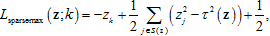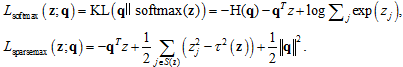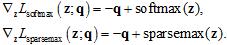From Softmax to Sparsemax-ICML16（1）

From Softmax toSparsemax: A Sparse Model of Attention and Multi-Label Classification

Authors: A. Martins and R. Astudillo

===========================

前言：前段时间扫了一下今年ICML的论文集。对于大部分ICML的论文，阅读是一种挑战，精读更需要相当的勇气。尽管如此，能啃下一两篇好文章必定会有所收获。接下来的几周，我会从今年ICML的论文集中挑选几篇个人觉得具有代表性（我所感兴趣）的文章做一些解读，分享阅读收获。今天挑选的这篇文章正好和前两次的内容“如何对Softmax函数的加速优化”是一个逻辑上的后续，就由此开始吧。

===================================

这篇文章的标题非常醒目—Softmax的稀疏化。我脑中浮现第一个问题：为什么要对Softmax进行稀疏化？结合文章内容给出我的个人理解：稀疏化Softmax的输出能更适合处理多标签问题。这里首先明确两个概念：多标签分类（mult-label classification）问题和多分类（multi-class classification）问题。多标签分类问题面对的实例可以属于多个标签，例如，一部电影可以是“韩国”、“动作”、“惊悚”。而多分类问题指的是一个实例有且仅属于多个分类中的一个。根据Softmax函数的形式化定义可知，Softmax函数更适合定义多分类问题。那么，如何转换Softmax函数的形式，使之适合多标签分类问题呢？

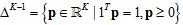
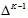
作者给出的答案是：假设真实的K个标签分类的分布p服从，其中是由自由度为K-1的概率分布p所定义的单纯形。则Sparsemax函数的损失为：

对比Softmax函数的形式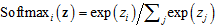：：首先Sparsemax的目标是直接逼近真实的多标签分类分布，另外Sparsemax不再由指数函数对输出z做smooth变换。采用直接将输出z投影到单纯形的方式能够起到输出的稀疏化效果（见补充材料）。

但以上Sparsemax的函数形式在真实分布未知的情况下并不能直接求解。通过拉格朗日法得到它的对偶形式：

其中[K]表示K个标签对应的下标集合。求解上式得，

 

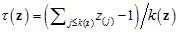
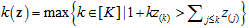
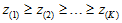
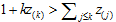
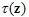
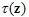
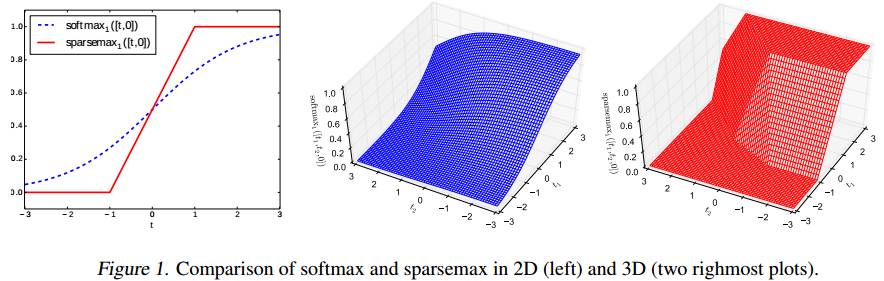
其中[t]₊=max{0,t}，，，。用语言形式描述Sparsemax的求解过程：1）将输出z按值降序排列；2）按序比较条件，若不满足则退出，求得满足条件的输出数k(z)；3）计算，并得到sparsemax_i。这里的也被称作关于z的阈值函数。通过在2维和3维空间上的示意图可以看到Sparsemax和Softmax的基本性质基本相同，在Sparsemax上基本保持了Softmax上的序关系，不同的是Sparsemax的输出不再平滑，头尾都被“截断”了。

图1 Softmax和Sparsemax在2维和3维空间中的示例对比

从Sparsemax在示例图上的表现形式上可以知道由Sparsemax函数定义的问题是非凸的优化问题。以Softmax为例，Softmax函数的对数似然损失为

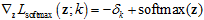
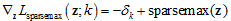
对应的梯度为：，其中δ_k为判断是否为分类目标的指示函数。但Sparsemax函数由于存在截断点，由于截断点的梯度不连续，有在截断点处的梯度不连续，被截断部分（值为0）的对数似然无法计算等问题，导致Sparsemax无法计算。因此文章提出了处处可导的凸函数Sparsemax Loss用来解决Sparsemax无法优化的问题。为了保持和Softmax函数梯度形式的一致性，定义Sparsemax Loss的梯度为：，根据这一梯度形式可得Sparsemax Loss的形式为：

其中S(z)是所有Sparsemax函数输出非负所对应的分类集合。

作者最后在多标签分类问题上做了扩展：在已知多标签分类问题的经验分布q的条件下，拟合经验分布。Softmax和Sparsemax在这一问题下的损失函数形式为：

对应的梯度为

实验部分我不做太多细节的描述，感兴趣的可以自行翻阅，说几点关于实验部分的个人总结：1）Sparsemax在实际问题中用来做多标签分类，并不一定能优于Softmax，也不一定优于Logistic回归；2）Sparsemax可以用来替换attention model中attention layer内的Softmax函数，增强权值的解释性，同时不降低原模型的性能。

>>补充材料<<：为什么Sparsemax能够产生稀疏化效果？

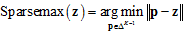
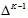
先从损失函数开始说起。这个损失函数的物理意义等价于将输出z投影到单纯形上，投影的方式为通过欧式距离找到距离单纯形上最近的一点，其投影点为p。由于单纯形的限制，导致这个投影点会大概率（相对于K维空间单纯形很小）落在单纯形的边界上，从而导致了稀疏化的效果。例如，在图 2的例子中，当2维空间中的投影点落在单纯形的边界上时即形成了稀疏化的输出结果。

图2 Sparsemax的稀疏化示例

 

总结：这篇文章的切入点准确，整体逻辑清晰，抛开那些不太友好的理论证明（ICML的风格），作者把主要脉络写得还挺易理解。缺憾在于Sparsemax对比Softmax和Logistic回归并没有在真实数据上取得突破，从对多标签分类问题的实验结果来看与其他两种方法相当，这使得文章并没有做到完全的首尾呼应。在由稀疏化所带来的可解释性上，Sparsemax在attention model中的应用算是一个亮点，这本身就是attention model提出初衷所试想解决的一个问题。