Deep Nonparametric Estimation of Intrinsic Data Structures by Chart Autoencoders: Generalization Error and Robustness

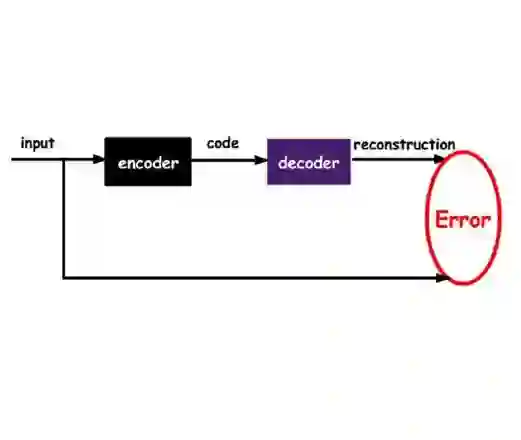
Autoencoders have demonstrated remarkable success in learning low-dimensional latent features of high-dimensional data across various applications. Assuming that data are sampled near a low-dimensional manifold, we employ chart autoencoders, which encode data into low-dimensional latent features on a collection of charts, preserving the topology and geometry of the data manifold. Our paper establishes statistical guarantees on the generalization error of chart autoencoders, and we demonstrate their denoising capabilities by considering $n$ noisy training samples, along with their noise-free counterparts, on a $d$-dimensional manifold. By training autoencoders, we show that chart autoencoders can effectively denoise the input data with normal noise. We prove that, under proper network architectures, chart autoencoders achieve a squared generalization error in the order of $\displaystyle n^{-\frac{2}{d+2}}\log^4 n$, which depends on the intrinsic dimension of the manifold and only weakly depends on the ambient dimension and noise level. We further extend our theory on data with noise containing both normal and tangential components, where chart autoencoders still exhibit a denoising effect for the normal component. As a special case, our theory also applies to classical autoencoders, as long as the data manifold has a global parametrization. Our results provide a solid theoretical foundation for the effectiveness of autoencoders, which is further validated through several numerical experiments.