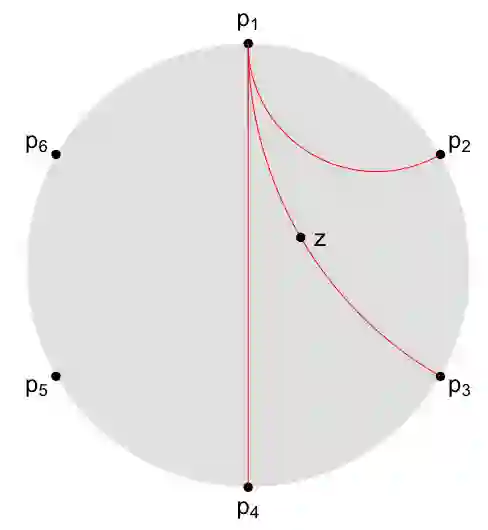
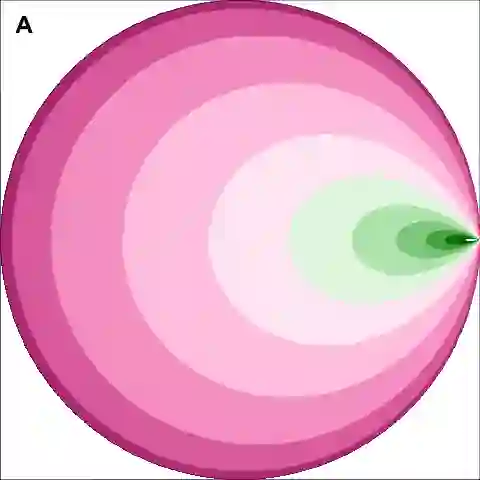
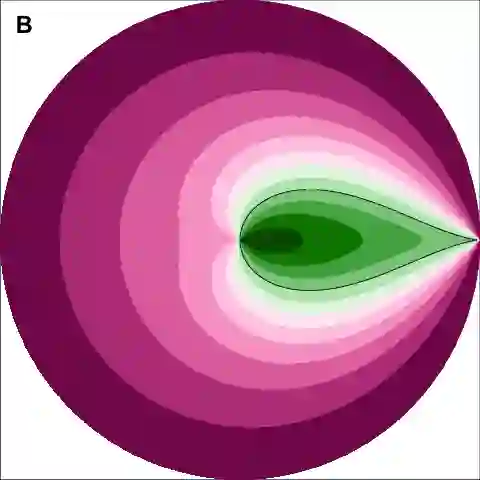
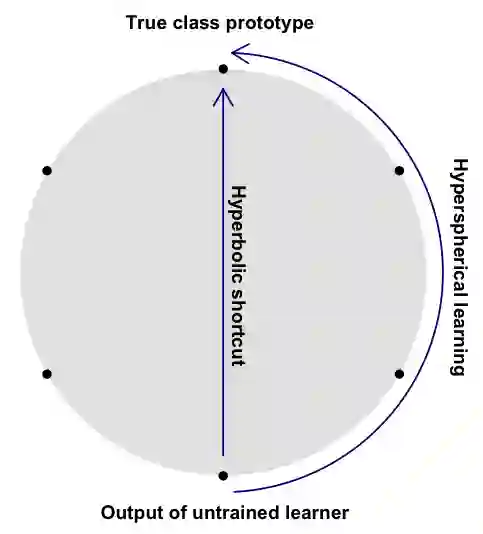
We introduce Hyperbolic Prototype Learning, a type of supervised learning, where class labels are represented by ideal points (points at infinity) in hyperbolic space. Learning is achieved by minimizing the 'penalized Busemann loss', a new loss function based on the Busemann function of hyperbolic geometry. We discuss several theoretical features of this setup. In particular, Hyperbolic Prototype Learning becomes equivalent to logistic regression in the one-dimensional case.
翻译:我们引入了超双曲原型学习, 这是一种受监督的学习类型, 类类标签在双曲空间中以理想点( 无限点) 来代表。 学习是通过最大限度地减少“ 被惩罚的Busemann损失 ” 实现的, 这是一种基于双曲几何的Busemann功能的新的损失函数。 我们讨论了这个设置的一些理论特征 。 特别是, 双曲原型学习等同于一维案例的后勤倒退 。
相关内容
专知会员服务
55+阅读 · 2020年7月3日
Arxiv
0+阅读 · 2020年11月23日
Arxiv
0+阅读 · 2020年11月20日
Arxiv
0+阅读 · 2020年11月19日