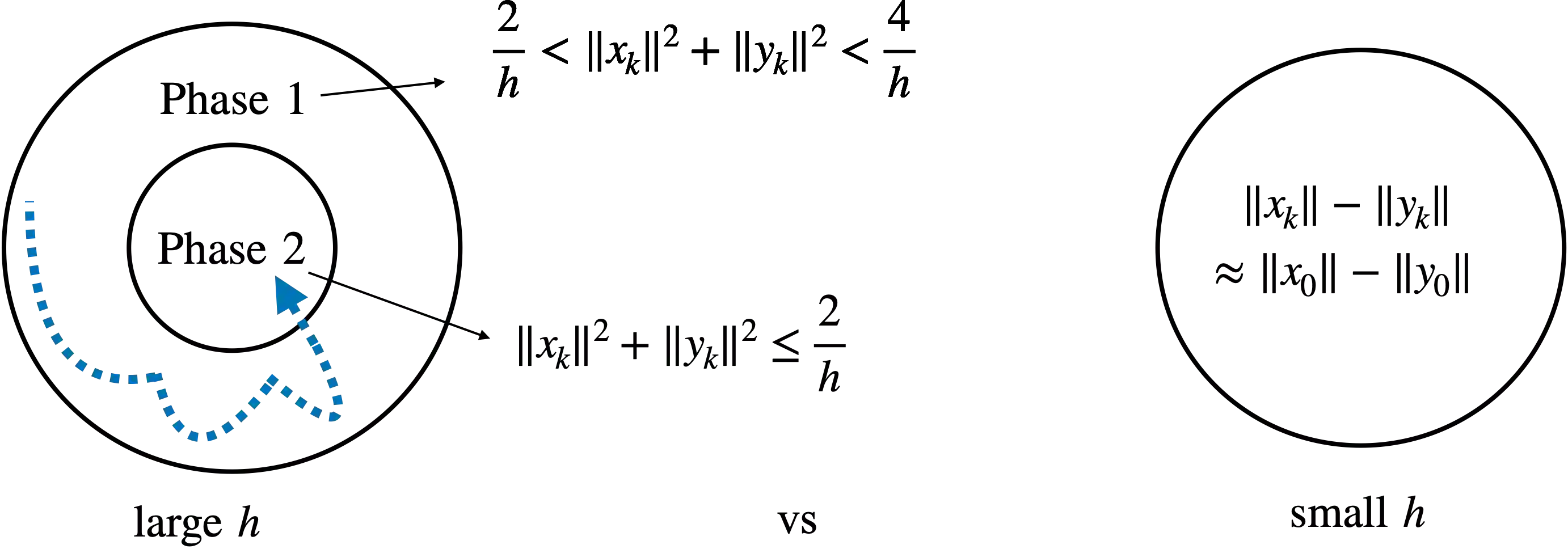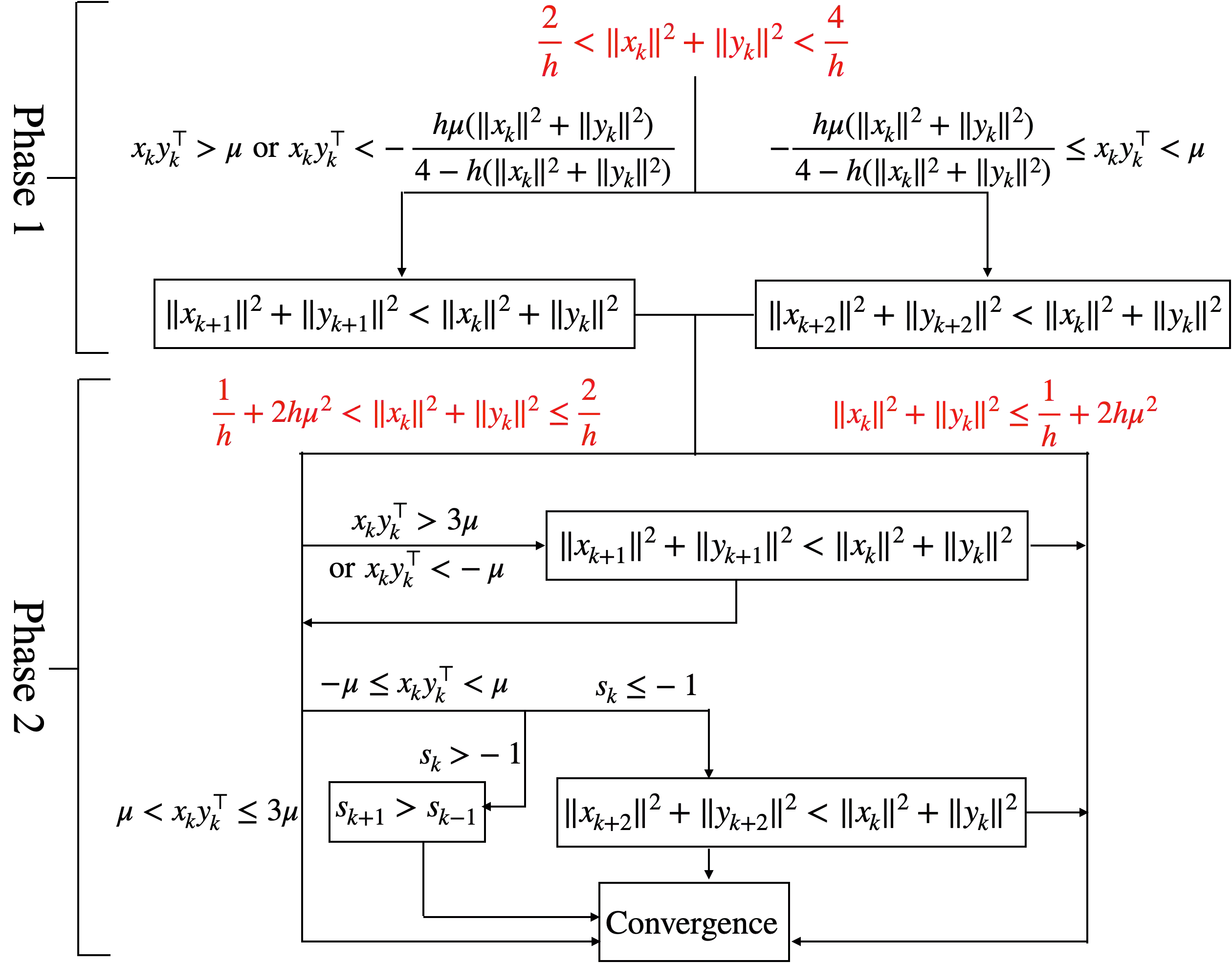Recent empirical advances show that training deep models with large learning rate often improves generalization performance. However, theoretical justifications on the benefits of large learning rate are highly limited, due to challenges in analysis. In this paper, we consider using Gradient Descent (GD) with a large learning rate on a homogeneous matrix factorization problem, i.e., $\min_{X, Y} \|A - XY^\top\|_{\sf F}^2$. We prove a convergence theory for constant large learning rates well beyond $2/L$, where $L$ is the largest eigenvalue of Hessian at the initialization. Moreover, we rigorously establish an implicit bias of GD induced by such a large learning rate, termed 'balancing', meaning that magnitudes of $X$ and $Y$ at the limit of GD iterations will be close even if their initialization is significantly unbalanced. Numerical experiments are provided to support our theory.
翻译:最近的实证进展表明,高学习率的深层次培训模式往往能提高一般化绩效。然而,由于分析方面的挑战,关于高学习率好处的理论依据非常有限。在本文中,我们考虑在单一的矩阵因子化问题上使用高学习率的梯子(GD),即$\min ⁇ X,Y} ⁇ A - XY ⁇ top ⁇ sf F ⁇ 2美元。我们证明,对于超过2美元/L$的恒定大型学习率,我们有一个趋同理论,因为美元是黑森在初始化时最大的叶素价值。此外,我们严格地确立了由如此庞大的学习率(称为“平衡 ”)引起的GD的隐含偏差,这意味着在GD迭代值极限的X$和Y$的幅度,即使其初始化严重失衡,也接近接近。提供了数字实验来支持我们的理论。