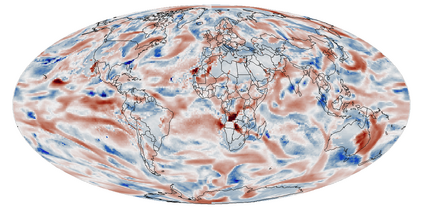
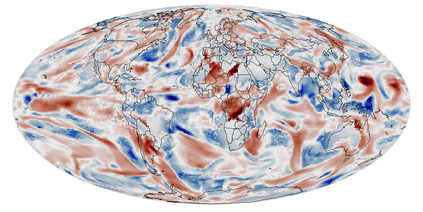
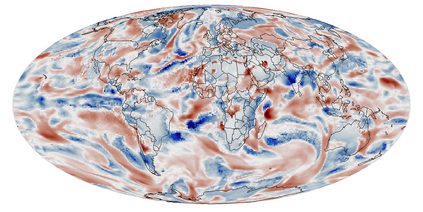
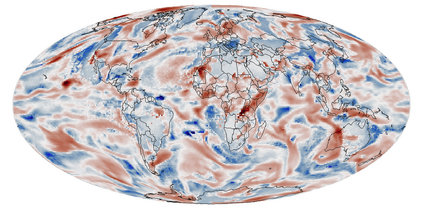
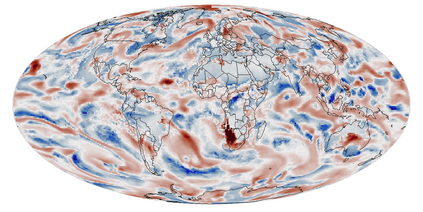
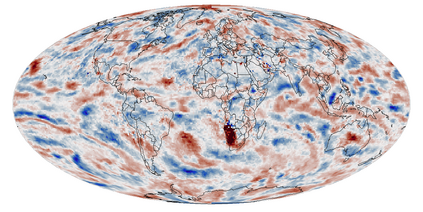
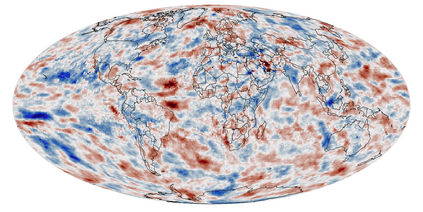
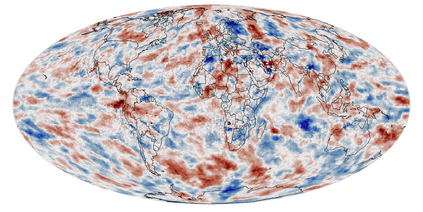
A multivariate distribution can be described by a triangular transport map from the target distribution to a simple reference distribution. We propose Bayesian nonparametric inference on the transport map by modeling its components using Gaussian processes. This enables regularization and accounting for uncertainty in the map estimation, while still resulting in a closed-form and invertible posterior map. We then focus on inferring the distribution of a nonstationary spatial field from a small number of replicates. We develop specific transport-map priors that are highly flexible but shrink toward a Gaussian field with Matern-type covariance. The approach is scalable to high-dimensional fields due to data-dependent sparsity and parallel computations. We also discuss extensions, including Dirichlet process mixtures for marginal non-Gaussianity. We present numerical results to demonstrate the accuracy, scalability, and usefulness of our methods, including statistical emulation of non-Gaussian climate-model output.
翻译:从目标分布到简单参考分布的三角运输图可以描述多变量分布。 我们建议使用高山进程对运输图的部件进行模型化,以此对运输图的部件进行贝叶斯非参数性推断。 这样可以对地图估计的不确定性进行正规化和衡算, 同时仍然产生一个封闭式和不可翻转的后方图。 然后我们侧重于从少量的复制中推断非静止空间场的分布。 我们开发了非常灵活但向高山域缩缩缩缩的特定的运输图前缀, 并带有母亲式的共变体。 由于依赖数据的宽度和平行计算, 这种方法可以向高维域伸缩。 我们还讨论扩展, 包括边际非加澳洲的dirichlet工艺混合物。 我们提出数字结果, 以显示我们方法的准确性、 可缩放性和有用性, 包括非加西气候模型产出的统计模拟。