Continuous logistic Gaussian random measure fields for spatial distributional modelling

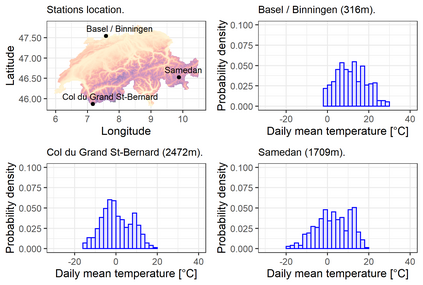
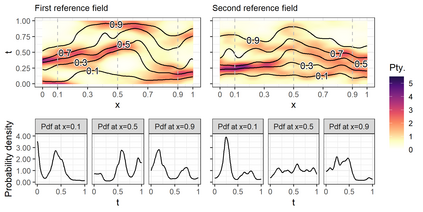
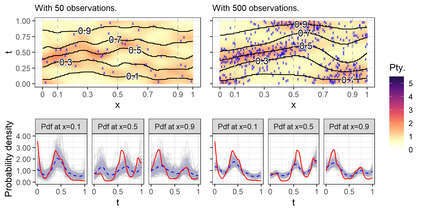
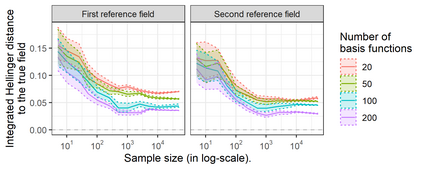
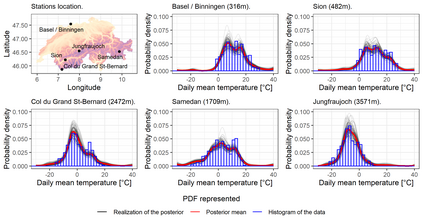
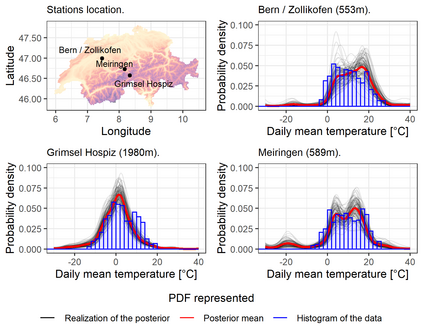
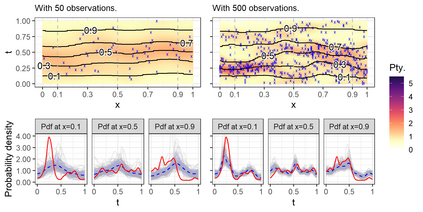
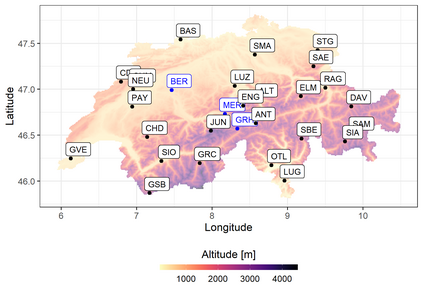
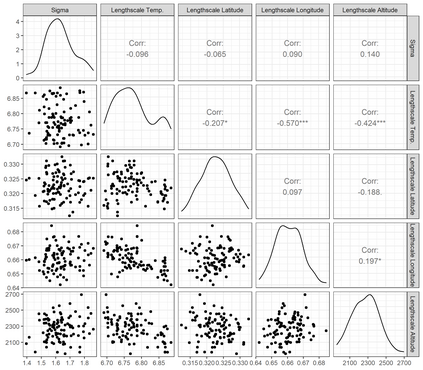
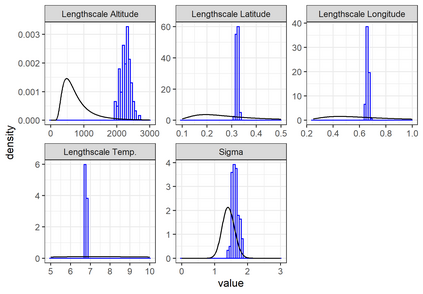
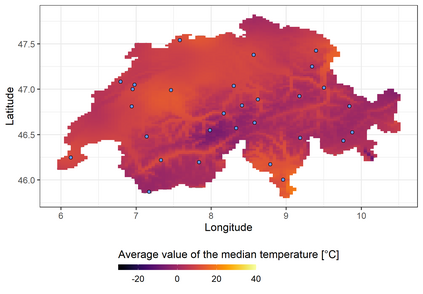
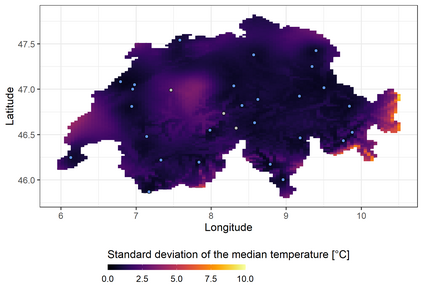
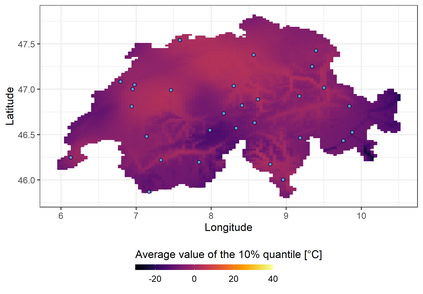
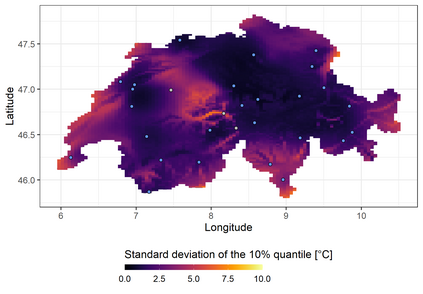
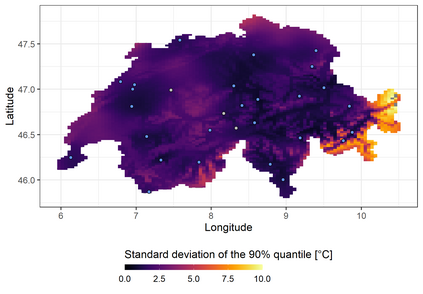
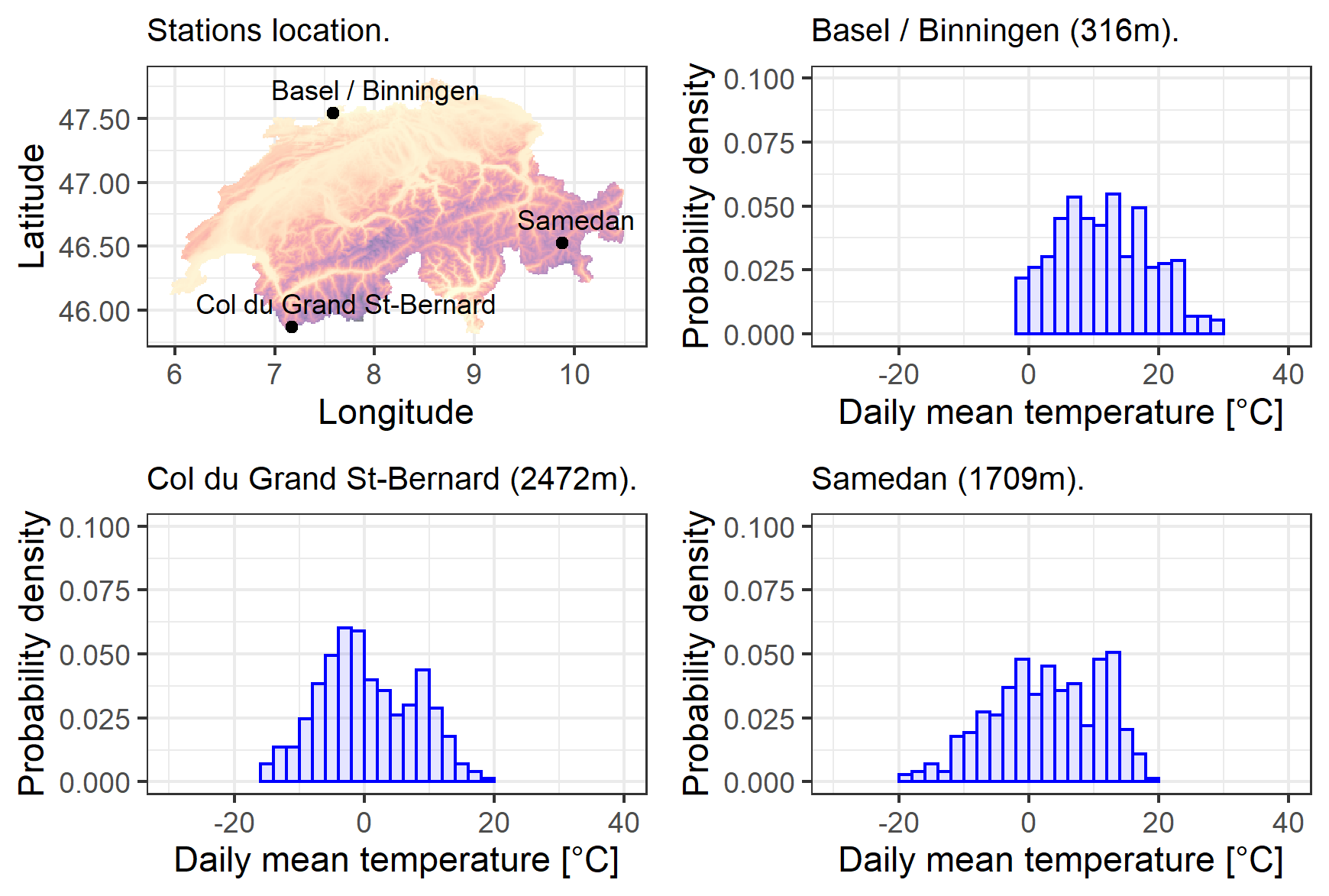
We investigate a class of models for non-parametric estimation of probability density fields based on scattered samples of heterogeneous sizes. The considered SLGP models are Spatial extensions of Logistic Gaussian Process (LGP) models and inherit some of their theoretical properties but also of their computational challenges. We revisit LGPs from the perspective of random measures and their densities, and investigate links between properties of LGPs and underlying processes. Turning to SLGPs is motivated by their ability to deliver probabilistic predictions of conditional distributions at candidate points, to allow (approximate) conditional simulations of probability densities, and to jointly predict multiple functionals of target distributions. We show that SLGP models induced by continuous GPs can be characterized by the joint Gaussianity of their log-increments and leverage this characterization to establish theoretical results pertaining to spatial regularity. We extend the notion of mean-square continuity to random measure fields and establish sufficient conditions on covariance kernels underlying SLGPs for associated models to enjoy such regularity properties. From the practical side, we propose an implementation relying on Random Fourier Features and demonstrate its applicability on synthetic examples and on temperature distributions at meteorological stations, including probabilistic predictions of densities at left-out stations.