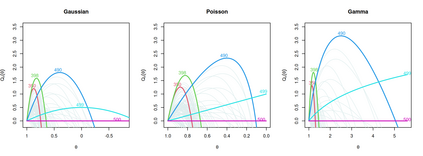
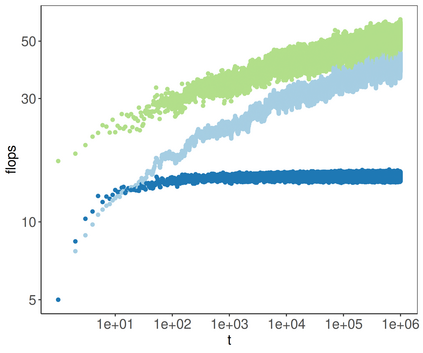
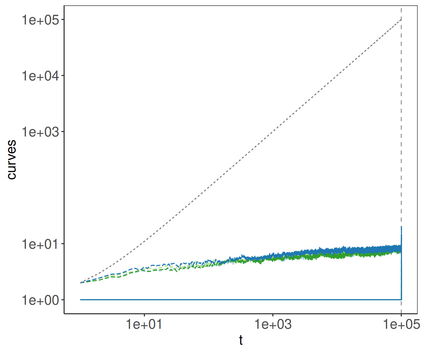
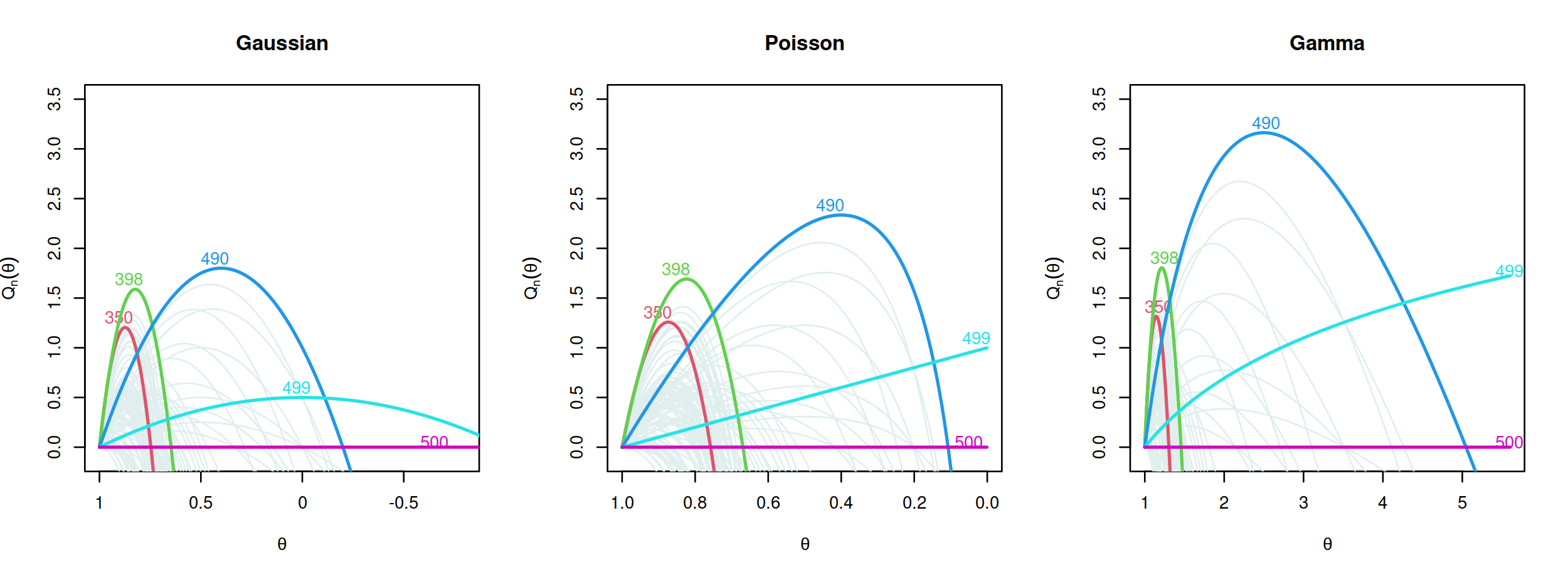
Online changepoint detection algorithms that are based on likelihood-ratio tests have been shown to have excellent statistical properties. However, a simple online implementation is computationally infeasible as, at time $T$, it involves considering $O(T)$ possible locations for the change. Recently, the FOCuS algorithm has been introduced for detecting changes in mean in Gaussian data that decreases the per-iteration cost to $O(\log T)$. This is possible by using pruning ideas, which reduce the set of changepoint locations that need to be considered at time $T$ to approximately $\log T$. We show that if one wishes to perform the likelihood ratio test for a different one-parameter exponential family model, then exactly the same pruning rule can be used, and again one need only consider approximately $\log T$ locations at iteration $T$. Furthermore, we show how we can adaptively perform the maximisation step of the algorithm so that we need only maximise the test statistic over a small subset of these possible locations. Empirical results show that the resulting online algorithm, which can detect changes under a wide range of models, has a constant-per-iteration cost on average.
翻译:以概率差测试为基础的在线变化点检测算法已证明具有极好的统计特性。 然而, 简单的在线实施在计算上是不可行的, 因为在时间上, 需要考虑$O( T) $ 的可能变化地点。 最近, 引入了 FOCuS 算法, 以检测高西亚数据平均值的变化, 从而将每通电成本降低到$O( log T) 。 使用修剪想法可以做到这一点, 从而将需要在时间上考虑的一组变化点位置降低到大约$\log T$。 我们显示, 如果有人希望对不同的一参数指数型家庭模型进行概率比测试, 那么可以使用完全相同的拼写规则, 并且人们再次只需要考虑大约$\ log T$ 。 此外, 我们展示了我们如何适应性地执行该算法的最大化步骤, 这样我们只需要在这些可能的小部分地点进行最大程度的测试统计。 Emprical 结果显示, 由此得出的在线算法在一系列模型下可以测出平均变化的成本。