Residual Tensor Train: a Flexible and Efficient Approach for Learning Multiple Multilinear Correlations

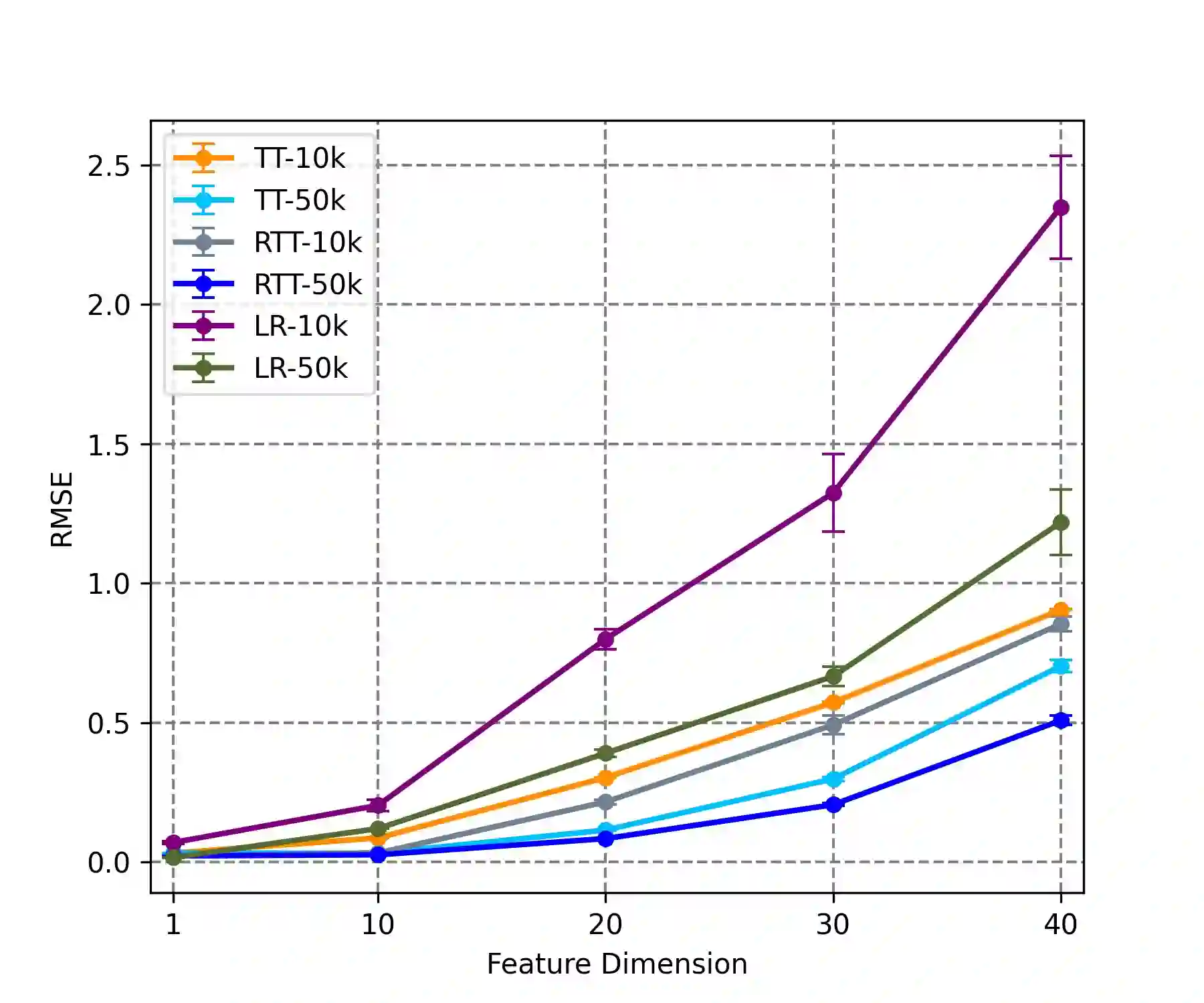
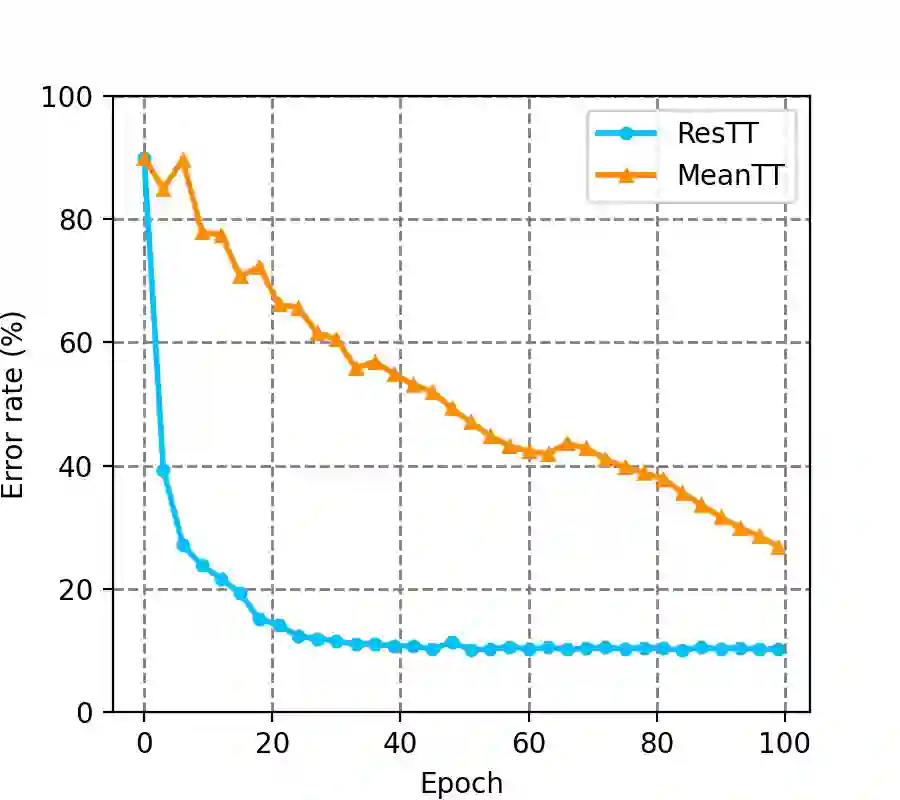
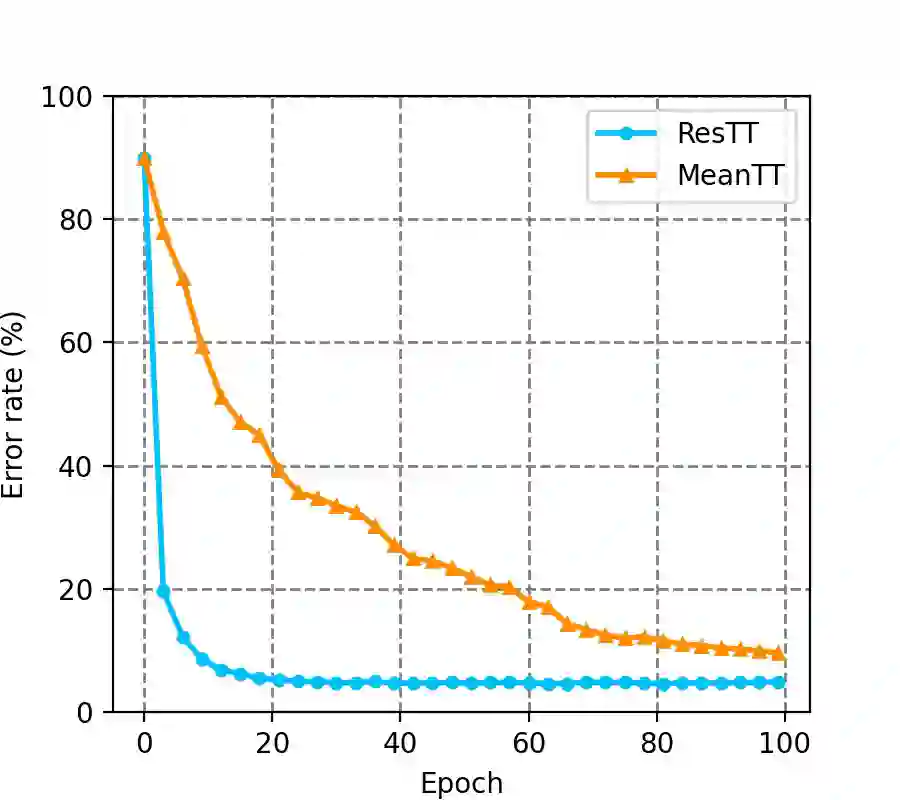
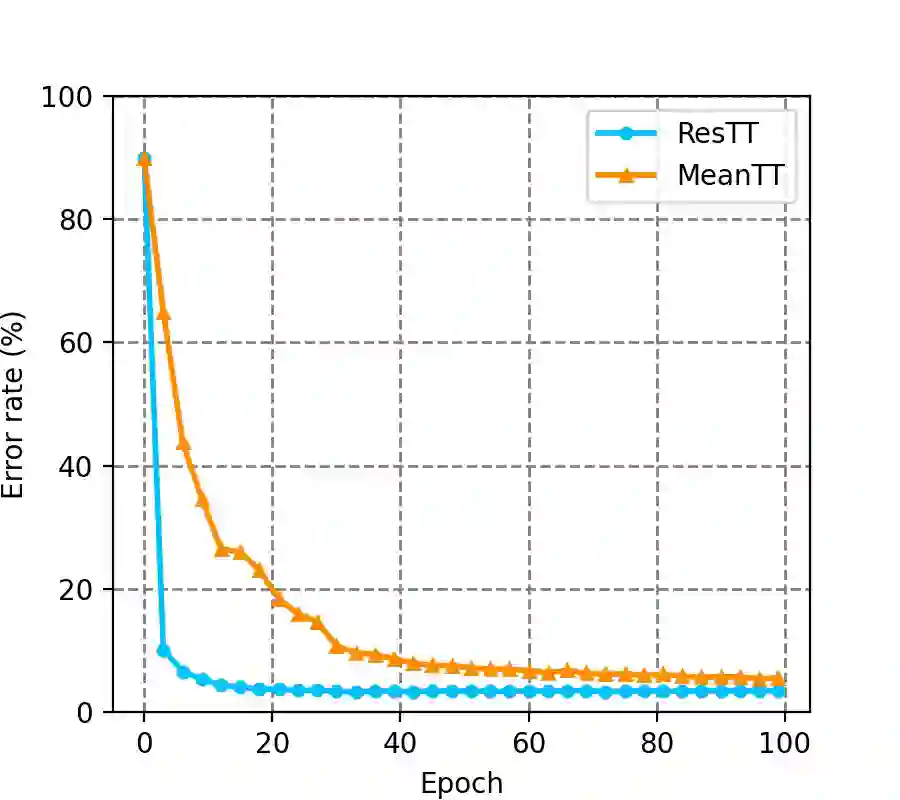
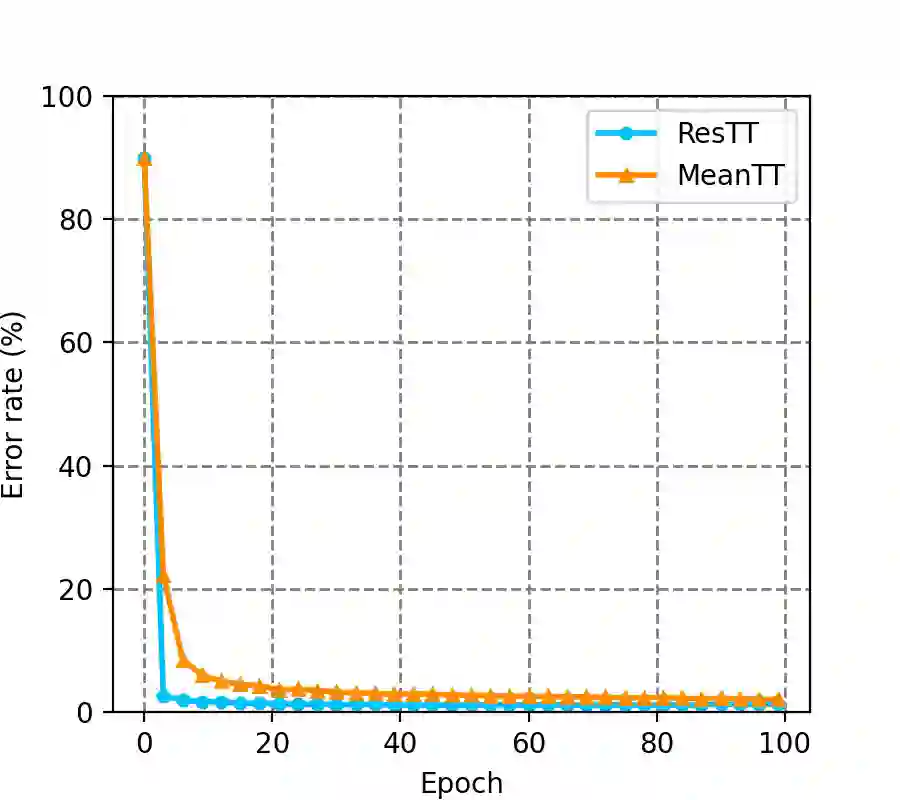
Tensor Train (TT) approach has been successfully applied in the modelling of the multilinear interaction of features. Nevertheless, the existing models lack flexibility and generalizability, as they only model a single type of high-order correlation. In practice, multiple multilinear correlations may exist within the features. In this paper, we present a novel Residual Tensor Train (ResTT) which integrates the merits of TT and residual structure to capture the multilinear feature correlations, from low to higher orders, within the same model. In particular, we prove that the fully-connected layer in neural networks and the Volterra series can be taken as special cases of ResTT. Furthermore, we derive the rule for weight initialization that stabilizes the training of ResTT based on a mean-field analysis. We prove that such a rule is much more relaxed than that of TT, which means ResTT can easily address the vanishing and exploding gradient problem that exists in the current TT models. Numerical experiments demonstrate that ResTT outperforms the state-of-the-art tensor network approaches, and is competitive with the benchmark deep learning models on MNIST and Fashion-MNIST datasets.