【ACML2020】张量网络机器学习:最近的进展和前沿，109页ppt

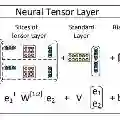
张量网络是由许多低阶张量组成的网络来表示高阶张量的有效方法，这些低阶张量网络在量子物理和应用数学中都有研究。近年来，TNs在机器学习中得到了越来越多的研究和应用，用于深度神经网络(DNNs)的高维数据分析、模型压缩和高效计算，以及对DNNs表达能力的理论分析。本教程旨在从TN数据表示、参数建模和函数逼近的角度介绍TNs技术应用于机器学习的最新进展。具体来说，我们将介绍TNs的基本模型和算法，无监督学习的典型方法，张量补全，多模态学习以及在DNN, CNN, RNN等中的各种应用。我们还讨论了这一研究领域的新前沿和未来趋势。

Part I. 张量方法数据表示 Tensor Methods for Data Representation Tensor Train and Tensor Ring Models Tensor Network Diagram Latent Convex Tensor Decomposition Tensor Completion for Missing Values Tensor Decomposition

Part II. 张量网络深度学习建模Tensor Networks in Deep Learning Modeling Applications to RNN, LSTM, and Transformer Multimodal Learning by Tensor Networks Tensor Networks for Theoretical Analysis of DNNs Speedup and Compression of CNN Exponential Machine Supervised Learning with Quantum Inspired Tensor Networks Learning Algorithms for Reparametrization by Tensor Networks Model Compression of NN by Tensor Networks

Part III. 前沿进展与趋势 Frontiers and Future Trends Discussions Structure Learning of Tensor Networks Supervised Learning by Multi-scale TNs, 2D PEPS type TNs, and Tree TNs Gaussian Mixture Distribution with Multi-dimensional Modes Generative Modeling by TN TN Representation for Probabilistic Graphical Model TN for Function Approximation of Supervised Learning