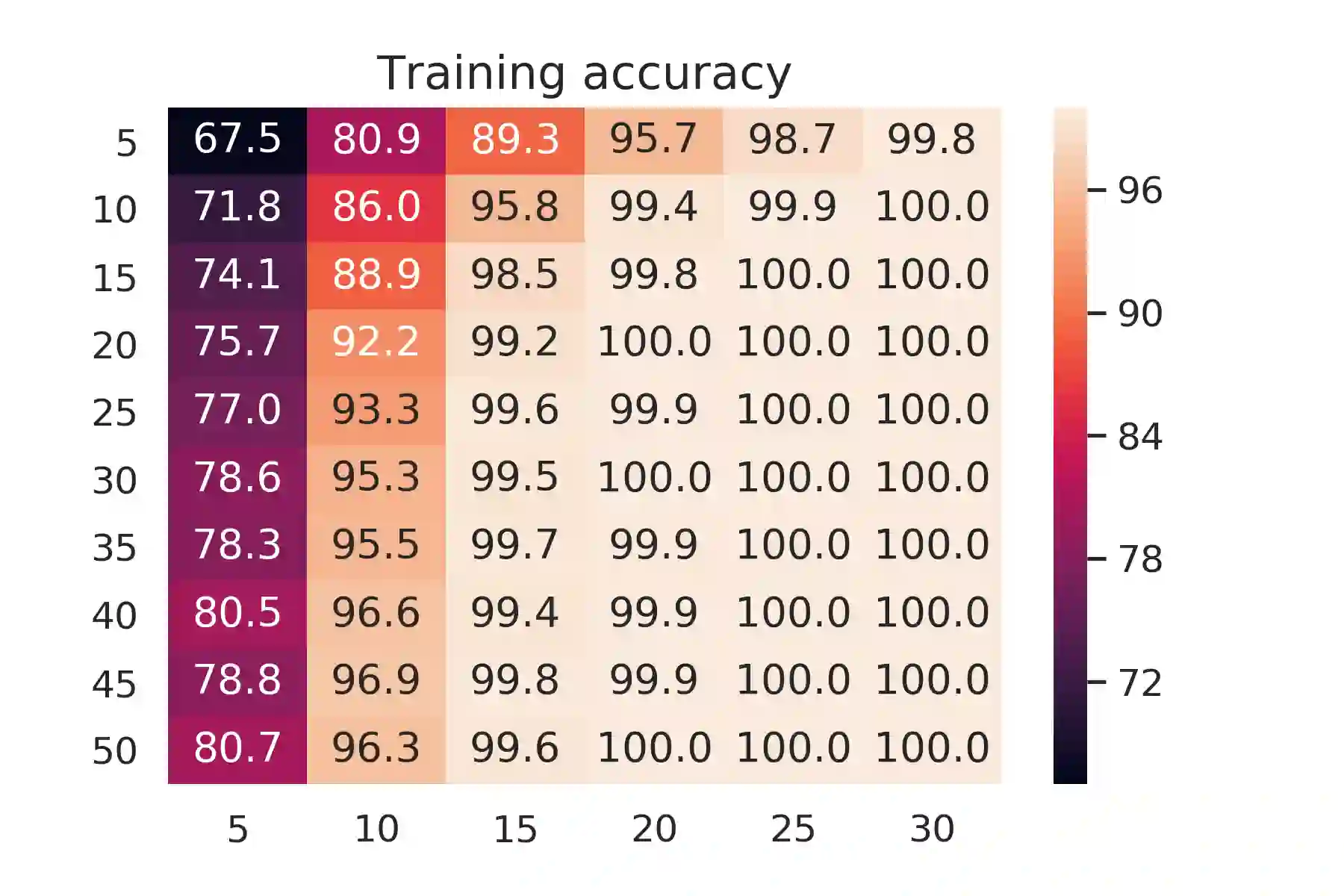
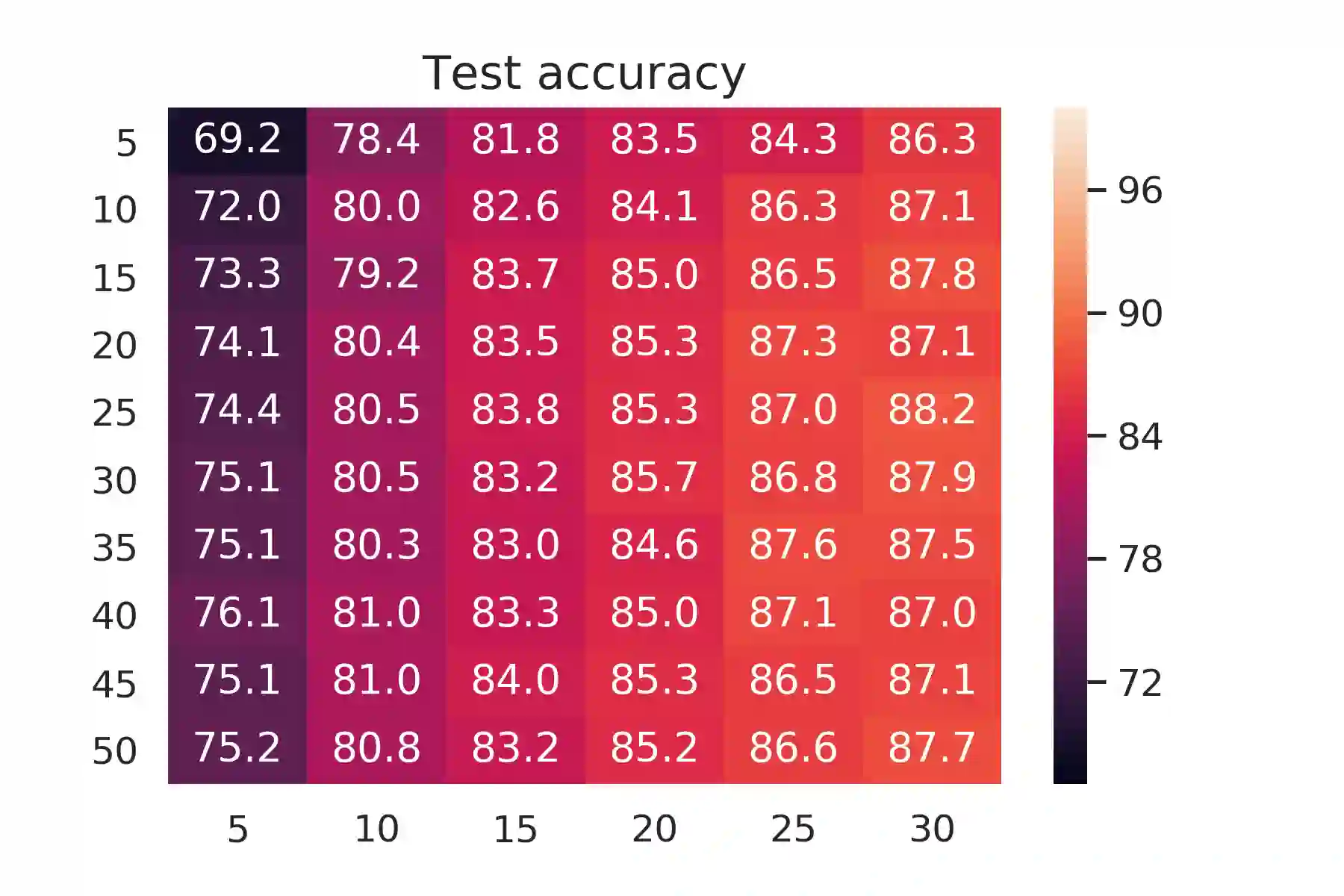
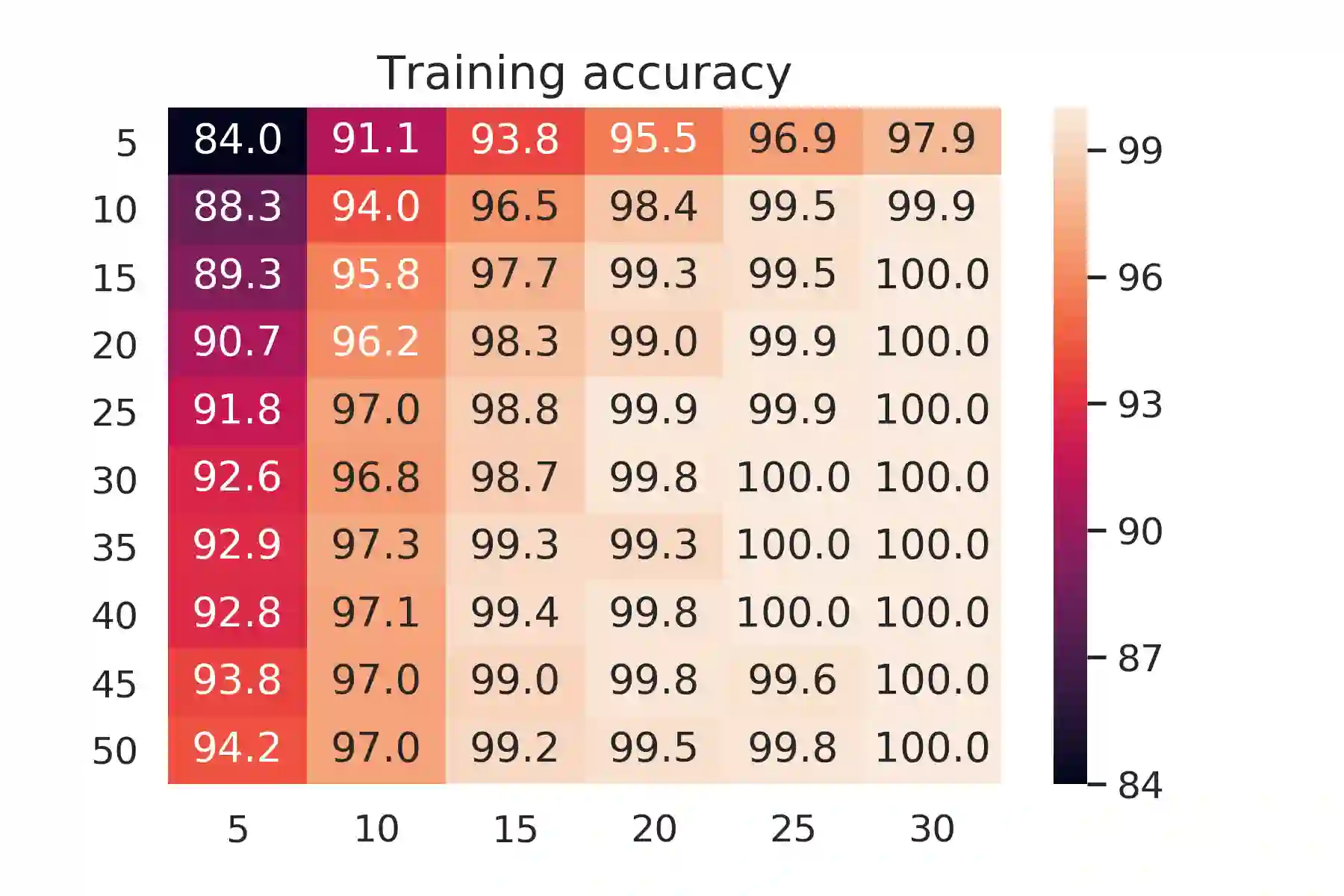
It is known that $O(N)$ parameters are sufficient for neural networks to memorize arbitrary $N$ input-label pairs. By exploiting depth, we show that $O(N^{2/3})$ parameters suffice to memorize $N$ pairs, under a mild condition on the separation of input points. In particular, deeper networks (even with width $3$) are shown to memorize more pairs than shallow networks, which also agrees with the recent line of works on the benefits of depth for function approximation. We also provide empirical results that support our theoretical findings.
翻译:众所周知, $O( N) 参数足以让神经网络记住任意的 $( N) 输入标签的配对。 通过深度开发, 我们发现, $( N ⁇ 2/3 }) 参数足以在输入点分离的温和条件下, 将一对美元作为一对, 特别是, 更深的网络( 即使宽度为3美元) 显示比浅层网络更能记住一对, 浅层网络也同意最近关于功能近似深度好处的工程线。 我们还提供了支持我们理论结论的经验性结果 。
相关内容
神经网络(Neural Networks)是世界上三个最古老的神经建模学会的档案期刊:国际神经网络学会(INNS)、欧洲神经网络学会(ENNS)和日本神经网络学会(JNNS)。神经网络提供了一个论坛,以发展和培育一个国际社会的学者和实践者感兴趣的所有方面的神经网络和相关方法的计算智能。神经网络欢迎高质量论文的提交,有助于全面的神经网络研究,从行为和大脑建模,学习算法,通过数学和计算分析,系统的工程和技术应用,大量使用神经网络的概念和技术。这一独特而广泛的范围促进了生物和技术研究之间的思想交流,并有助于促进对生物启发的计算智能感兴趣的跨学科社区的发展。因此,神经网络编委会代表的专家领域包括心理学,神经生物学,计算机科学,工程,数学,物理。该杂志发表文章、信件和评论以及给编辑的信件、社论、时事、软件调查和专利信息。文章发表在五个部分之一:认知科学,神经科学,学习系统,数学和计算分析、工程和应用。
官网地址:http://dblp.uni-trier.de/db/journals/nn/
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
10+阅读 · 2021年10月17日
Arxiv
13+阅读 · 2020年6月24日