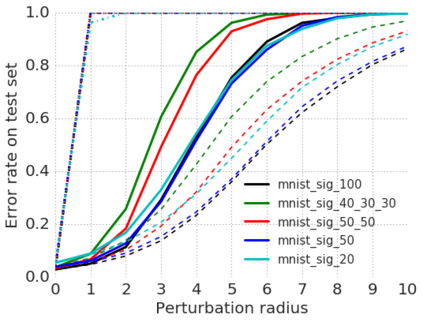
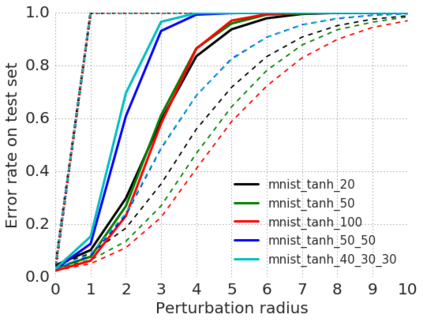
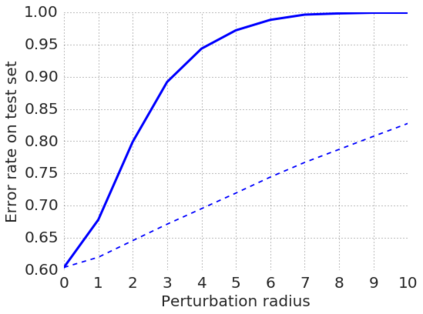
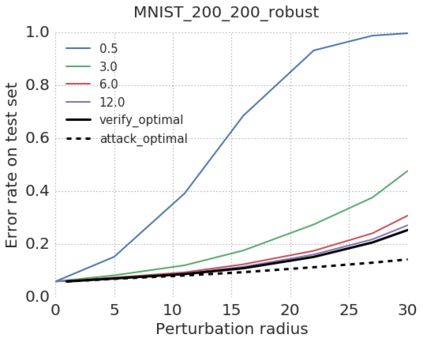
This paper addresses the problem of formally verifying desirable properties of neural networks, i.e., obtaining provable guarantees that neural networks satisfy specifications relating their inputs and outputs (robustness to bounded norm adversarial perturbations, for example). Most previous work on this topic was limited in its applicability by the size of the network, network architecture and the complexity of properties to be verified. In contrast, our framework applies to a general class of activation functions and specifications on neural network inputs and outputs. We formulate verification as an optimization problem (seeking to find the largest violation of the specification) and solve a Lagrangian relaxation of the optimization problem to obtain an upper bound on the worst case violation of the specification being verified. Our approach is anytime i.e. it can be stopped at any time and a valid bound on the maximum violation can be obtained. We develop specialized verification algorithms with provable tightness guarantees under special assumptions and demonstrate the practical significance of our general verification approach on a variety of verification tasks.
翻译:本文论述正式核实神经网络适当特性的问题,即获得神经网络满足其投入和产出规格的可证实的保证(例如,对约束性规范的对抗性扰动的野蛮行为),以前关于这一专题的大部分工作由于网络的规模、网络结构以及有待核实的特性的复杂性而对其适用性有所限制。相反,我们的框架适用于神经网络投入和产出的激活功能和规格的一般类别。我们把核查作为一个优化问题(寻求找到最大的违反规格的情况)来拟订,并解决优化问题的拉格朗加省放松问题,以便在最坏的违反所核查的规格的情况上获得上限。我们的方法是随时可以停止的,并且可以取得关于最大违反的有效的约束。我们开发了专门的核查算法,在特别假设下有可证实的严格性保证,并表明我们对各种核查任务的一般核查方法的实际意义。