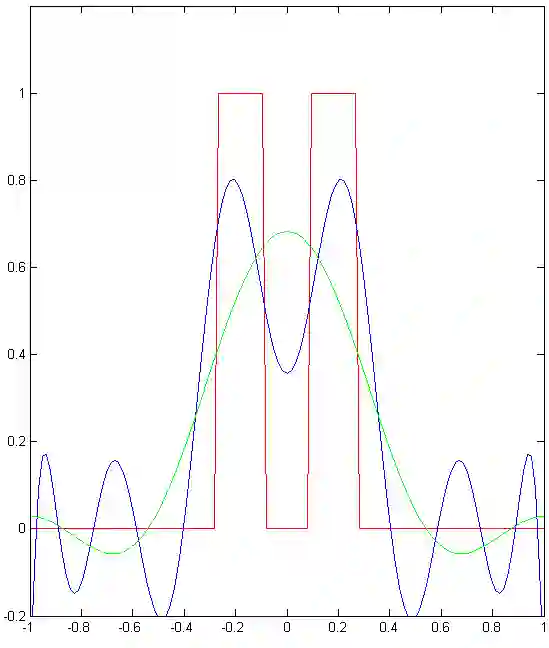
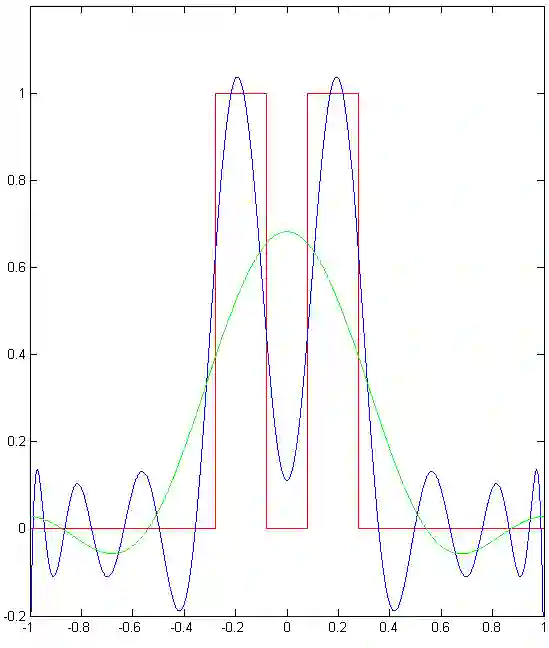
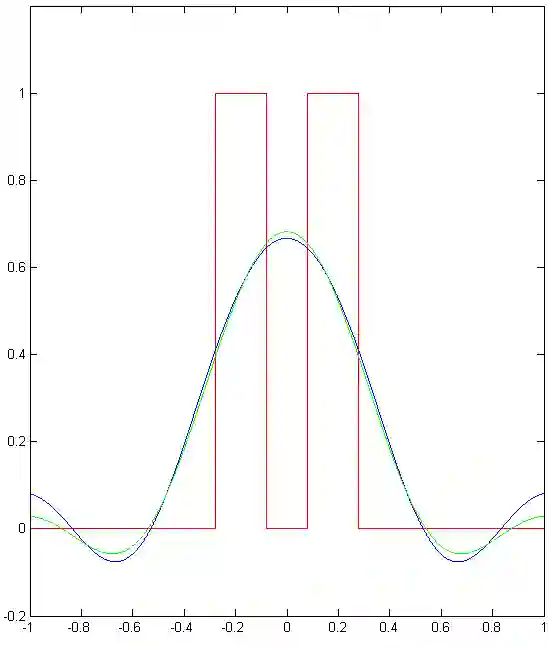
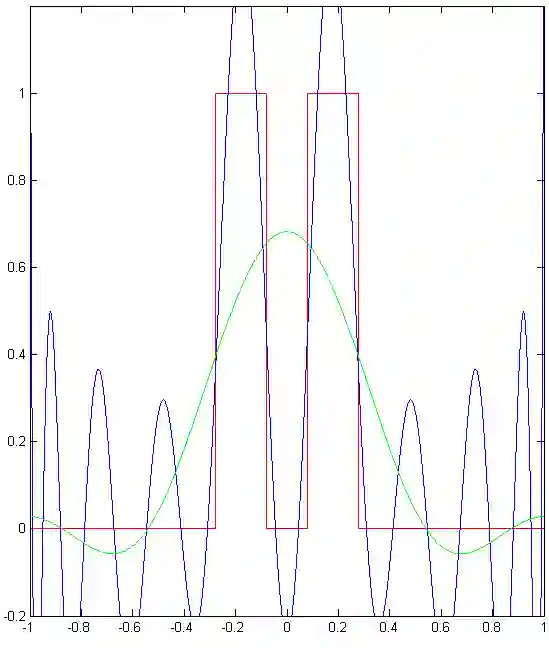
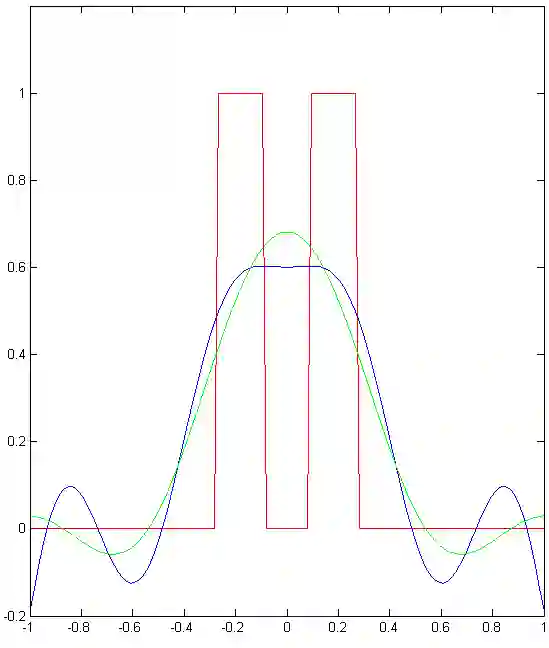
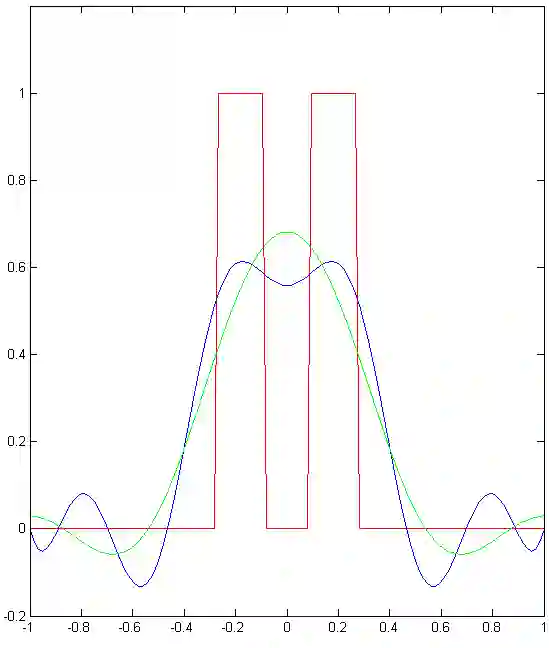
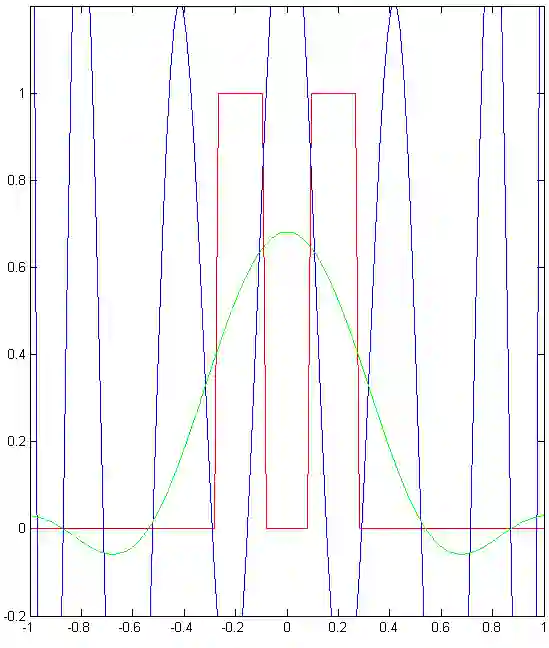
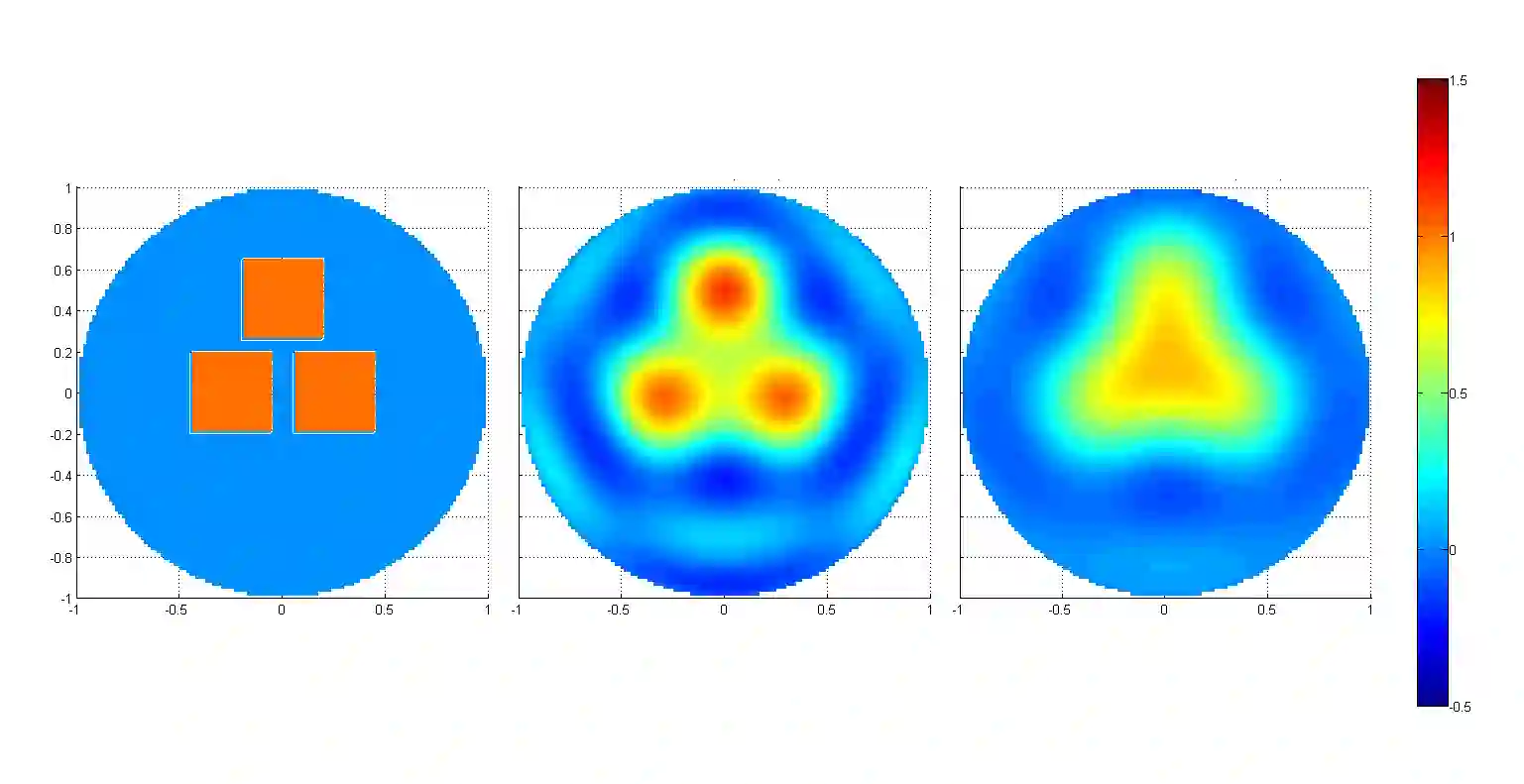
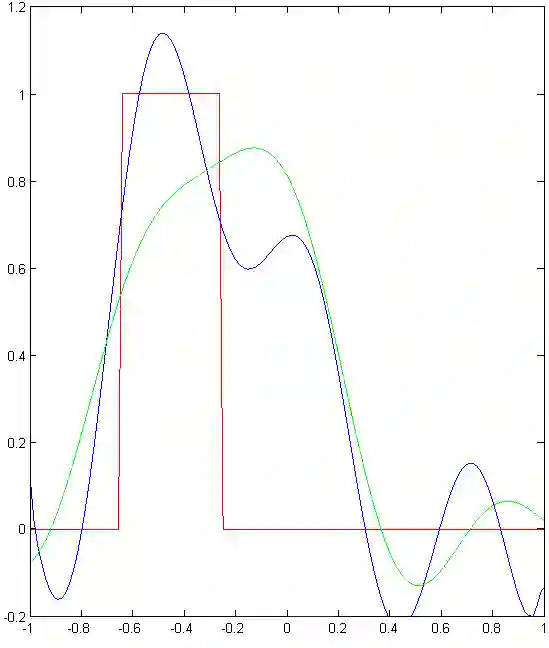
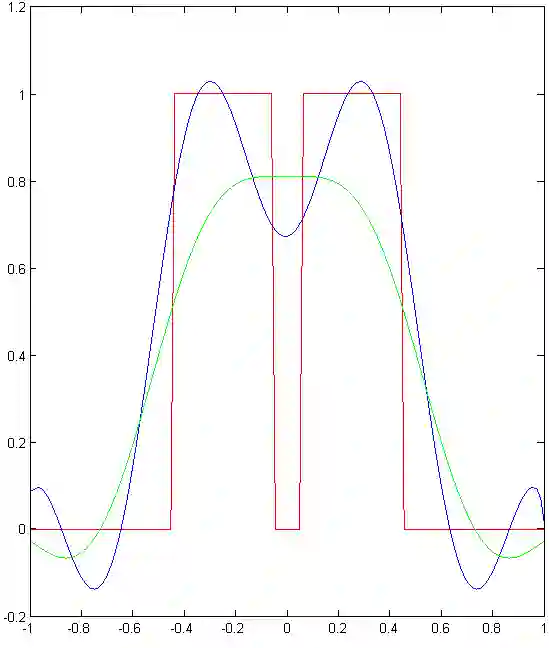
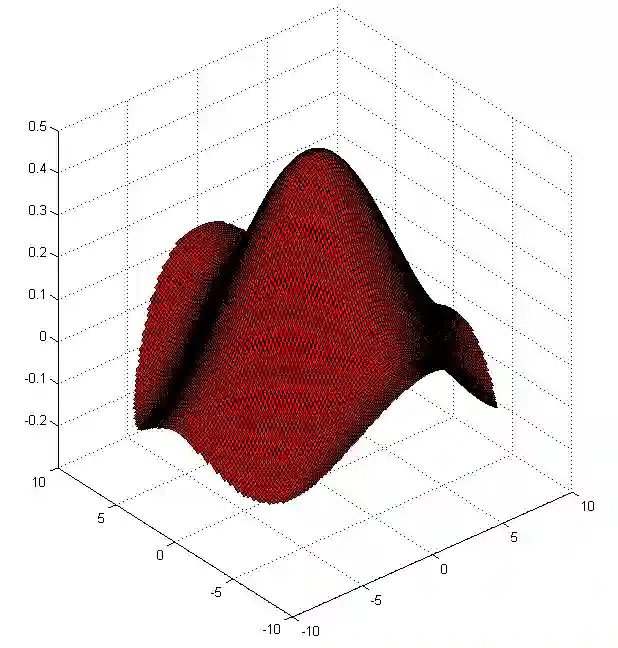
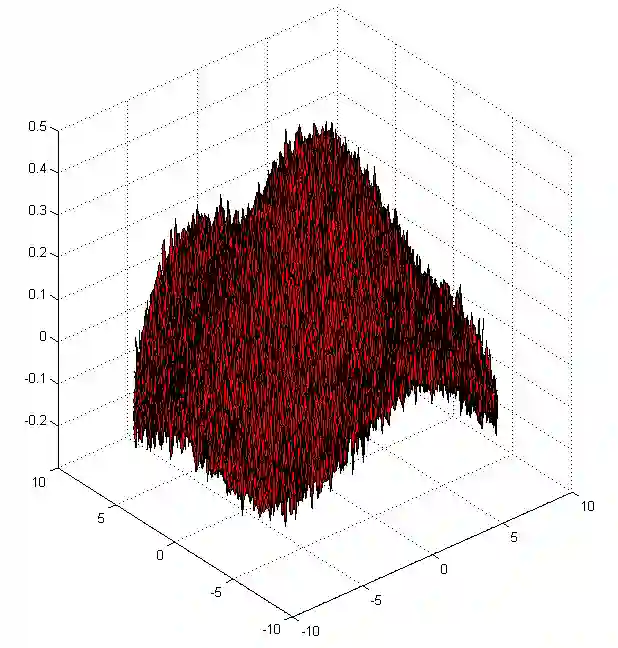
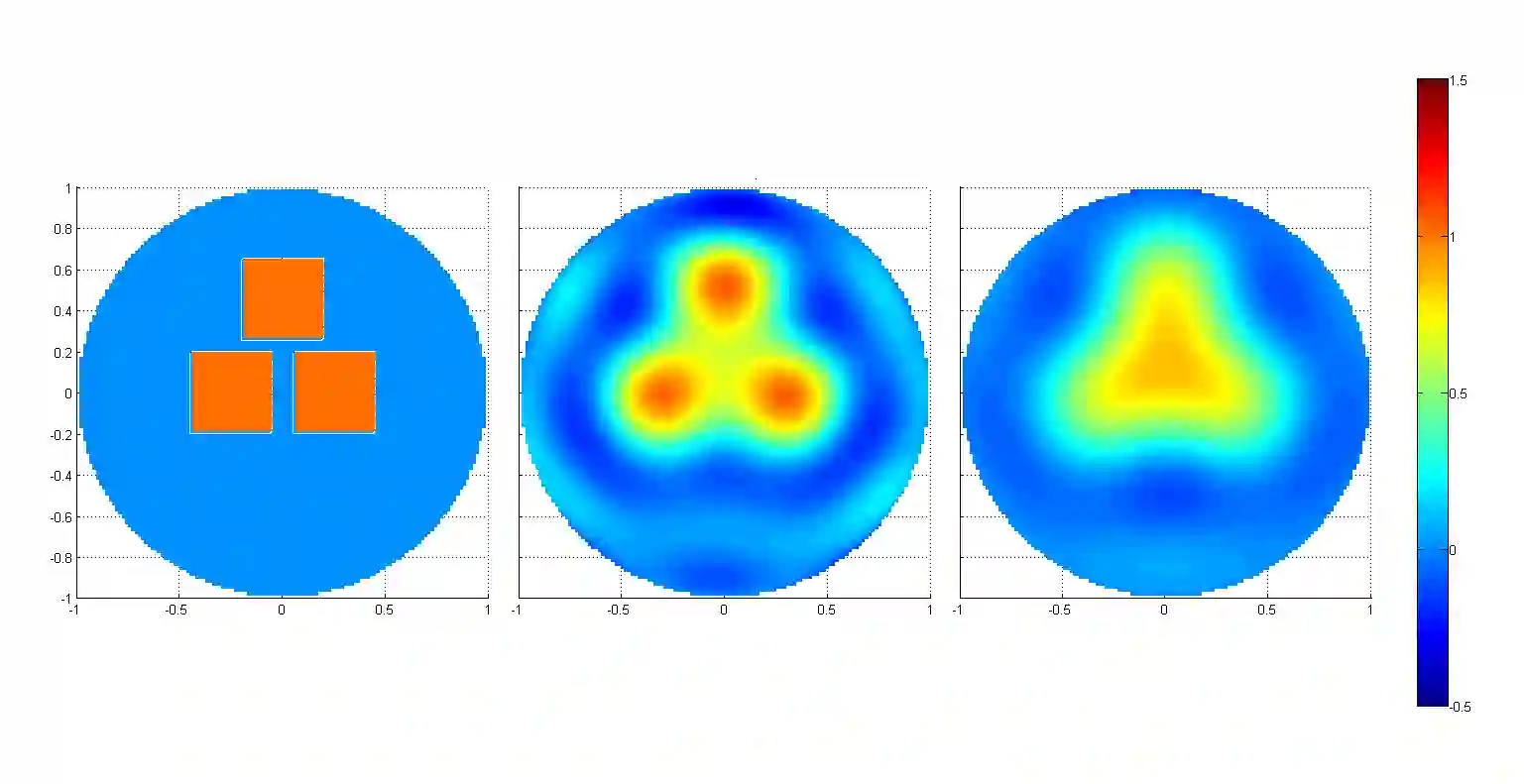
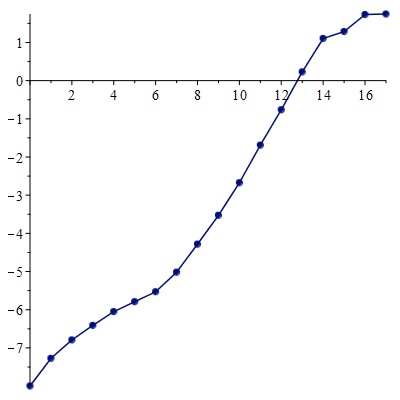
We implement numerically formulas of [Isaev, Novikov, arXiv:2107.07882] for finding a compactly supported function $v$ on $\mathbb{R}^d$, $d\geq 1$, from its Fourier transform $\mathcal{F} [v]$ given within the ball $B_r$. For the one-dimensional case, these formulas are based on the theory of prolate spheroidal wave functions, which arise, in particular, in the singular value decomposition of the aforementioned band-limited Fourier transform for $d = 1$. In multidimensions, these formulas also include inversion of the Radon transform. In particular, we give numerical examples of super-resolution, that is, recovering details beyond the diffraction limit.
翻译:我们实施了[Isaev, Novikov, arXiv: 2107.7882] 的数值公式,用于从Fourier 变换 $\ mathbb{R ⁇ d$, $d\geq 1$ 中找到一个由压实支持的函数, 以美元为单位, 美元为单位, 美元为单位, 美元为单位, 美元为美元, 美元为美元, 美元为美元, 美元为1美元。 对于一维的情况, 这些公式基于预造的类固波函数理论, 特别是上述带宽Fourier 变换的单值, 以美元= 1美元为单位。 在多维值中, 这些公式还包括反转 Radon 变换。 特别是, 我们给出了超分辨率的数字例子, 也就是, 恢复细节的超分解限度之外。