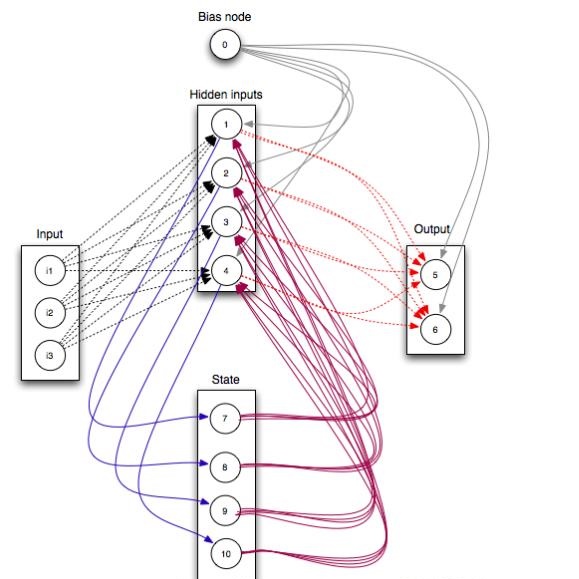
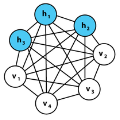
Understanding the dynamics of a system is important in many scientific and engineering domains. This problem can be approached by learning state transition rules from observations using machine learning techniques. Such observed time-series data often consist of sequences of many continuous variables with noise and ambiguity, but we often need rules of dynamics that can be modeled with a few essential variables. In this work, we propose a method for extracting a small number of essential hidden variables from high-dimensional time-series data and for learning state transition rules between these hidden variables. The proposed method is based on the Restricted Boltzmann Machine (RBM), which treats observable data in the visible layer and latent features in the hidden layer. However, real-world data, such as video and audio, include both discrete and continuous variables, and these variables have temporal relationships. Therefore, we propose Recurrent Temporal GaussianBernoulli Restricted Boltzmann Machine (RTGB-RBM), which combines Gaussian-Bernoulli Restricted Boltzmann Machine (GB-RBM) to handle continuous visible variables, and Recurrent Temporal Restricted Boltzmann Machine (RT-RBM) to capture time dependence between discrete hidden variables. We also propose a rule-based method that extracts essential information as hidden variables and represents state transition rules in interpretable form. We conduct experiments on Bouncing Ball and Moving MNIST datasets to evaluate our proposed method. Experimental results show that our method can learn the dynamics of those physical systems as state transition rules between hidden variables and can predict unobserved future states from observed state transitions.
翻译:了解一个系统的动态在许多科学和工程领域非常重要。 这个问题可以通过从机器学习技术的观测中学习国家转换规则来解决。 观察到的时间序列数据通常由许多连续变量序列组成, 充满噪音和模糊, 但我们经常需要能够以几个基本变量建模的动态规则。 因此, 我们建议了一种方法, 从高维时间序列数据中提取少量基本隐藏变量, 并学习这些隐藏变量之间的转换规则。 提议的方法基于“ 限制的 Boltzmann 预测机器 ” ( RBM ), 它处理可见层中的可见数据, 隐藏层中的潜伏特性。 然而, 真实世界数据, 如视频和音频, 包括离散和连续的变量, 并且这些变量有时间关系。 因此, 我们提议了一个方法, 从高尚- 贝诺曼 限制 机器( RT- RBMM ) 中提取少量的隐藏的隐藏变量 。 将高斯- 伯尔努里诺里斯特里斯特里· 巴鲁曼机器 (GBM ) 用于处理持续可见变量之间的变量, 。 以及 经常性的 隐性 限制的 Bolzmann 变变换规则 规则, 显示我们隐性规则 和变变变法 。 我们的变法 显示的变法, 以 以 以 隐藏的变法 隐藏的变法 以 以 以 显示的 显示的 变变法 变法, 我们的变法, 变法 变法 。