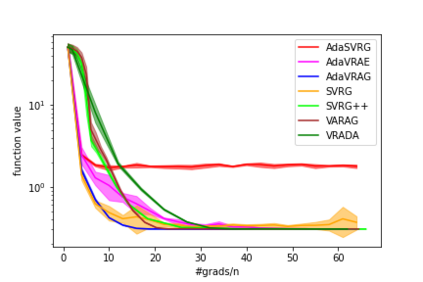
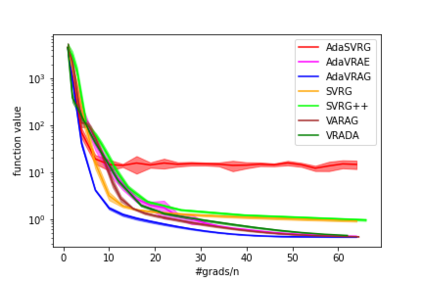
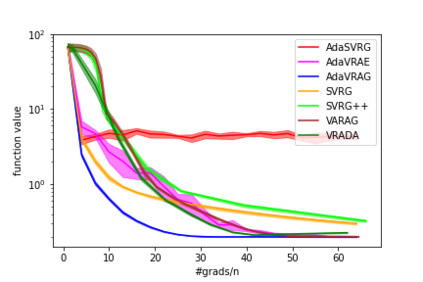
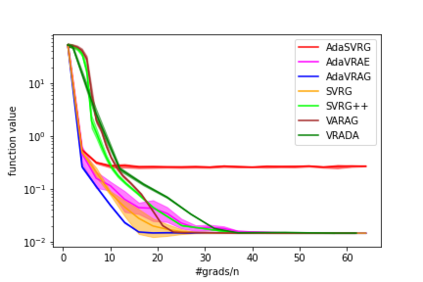
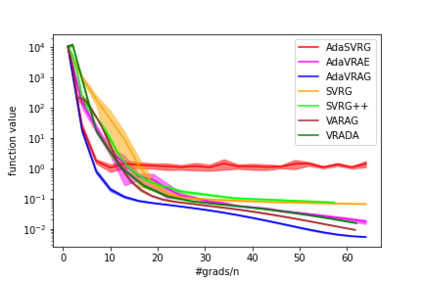
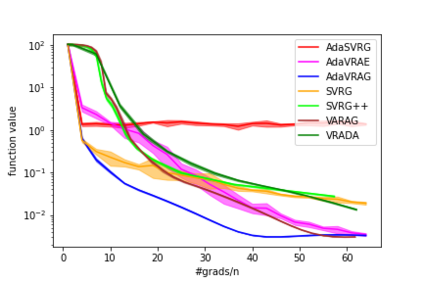
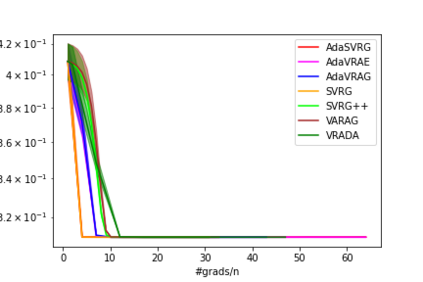
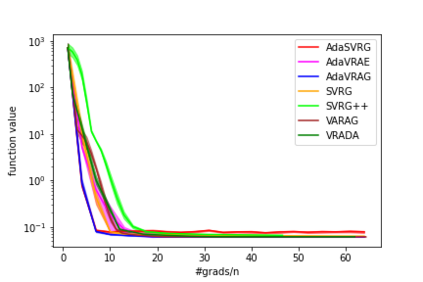
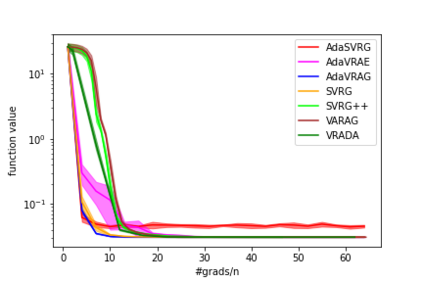
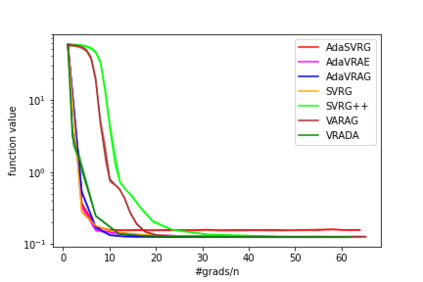
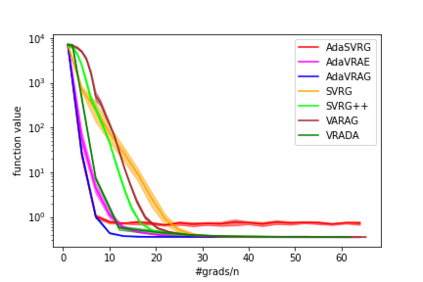
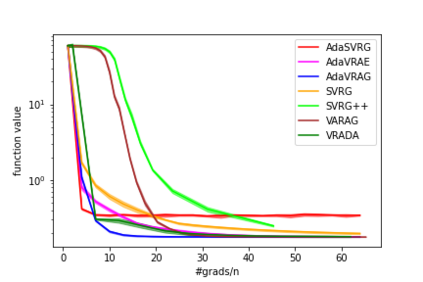
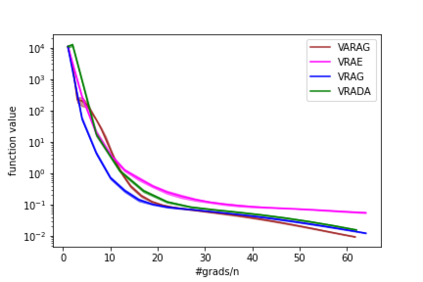
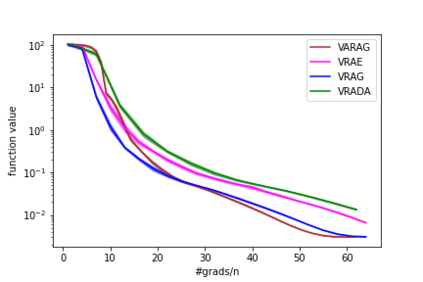
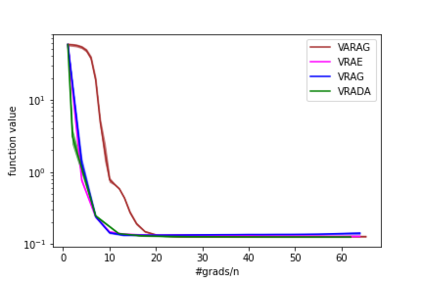
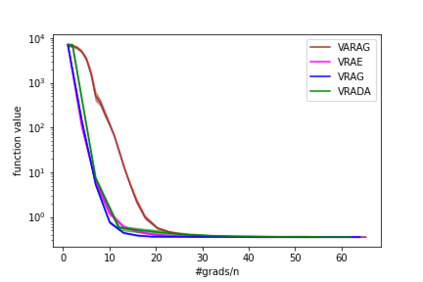
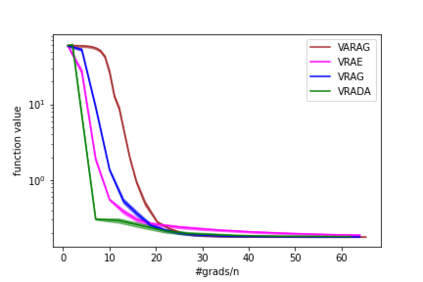
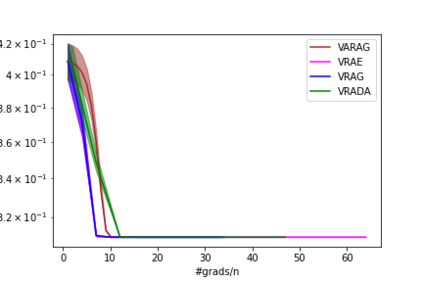
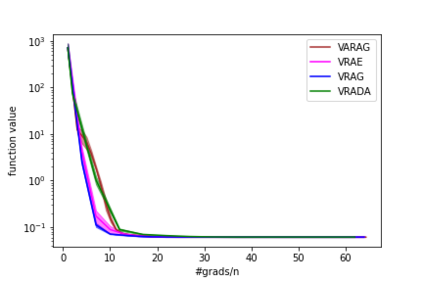
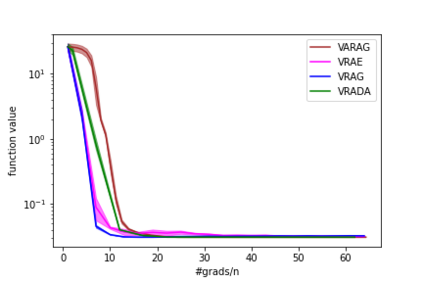
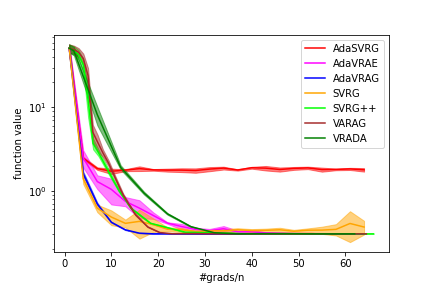
In this paper, we study the finite-sum convex optimization problem focusing on the general convex case. Recently, the study of variance reduced (VR) methods and their accelerated variants has made exciting progress. However, the step size used in the existing VR algorithms typically depends on the smoothness parameter, which is often unknown and requires tuning in practice. To address this problem, we propose two novel adaptive VR algorithms: Adaptive Variance Reduced Accelerated Extra-Gradient (AdaVRAE) and Adaptive Variance Reduced Accelerated Gradient (AdaVRAG). Our algorithms do not require knowledge of the smoothness parameter. AdaVRAE uses $\mathcal{O}\left(n\log\log n+\sqrt{\frac{n\beta}{\epsilon}}\right)$ gradient evaluations and AdaVRAG uses $\mathcal{O}\left(n\log\log n+\sqrt{\frac{n\beta\log\beta}{\epsilon}}\right)$ gradient evaluations to attain an $\mathcal{O}(\epsilon)$-suboptimal solution, where $n$ is the number of functions in the finite sum and $\beta$ is the smoothness parameter. This result matches the best-known convergence rate of non-adaptive VR methods and it improves upon the convergence of the state of the art adaptive VR method, AdaSVRG. We demonstrate the superior performance of our algorithms compared with previous methods in experiments on real-world datasets.
翻译:在本文中, 我们以一般 convex 案例为重点, 研究定时和 convex 优化问题。 最近, 对差异减少方法及其加速变异的研究取得了令人兴奋的进展。 但是, 现有的 VR 算法所使用的步数大小通常取决于平滑参数, 而这通常并不为人所知, 需要在实践中加以调整。 为了解决这个问题, 我们建议了两个新的适应性 VR 算法: 适应性差异减少加速异常值( AdaVRAE) 和适应性差异减少加速渐变( AdaVRAG) 。 我们的算法并不需要了解平滑度参数。 AdaVRE 使用 mathcal{ O ⁇ rft} 来计算平滑度参数, 梯值评价和 AdaVRG 使用 mathal =lental leg (n) laftal discal) = Vlational- discoal- ladeal$ 。 在 Vlational- ladeal roval roup roup roup roup roup roup roup roup roup roup roup et et roup roup roup roup roup,, rodal disl disl disl disal disl disl roisal rodal = Vl rodal rodal rodal = rodal rodal = 和前Vl rodaldal = 美元, 前的前V = rodal_ 和前VI 美元 rodal = rodaldaldal_ = = = = = = = ============ = = = = = ===============================================================================