Artificial neural networks and time series of counts: A class of nonlinear INGARCH models

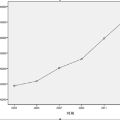
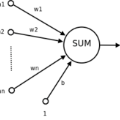
Time series of counts are frequently analyzed using generalized integer-valued autoregressive models with conditional heteroskedasticity (INGARCH). These models employ response functions to map a vector of past observations and past conditional expectations to the conditional expectation of the present observation. In this paper, it is shown how INGARCH models can be combined with artificial neural network (ANN) response functions to obtain a class of nonlinear INGARCH models. The ANN framework allows for the interpretation of many existing INGARCH models as a degenerate version of a corresponding neural model. Details on maximum likelihood estimation, marginal effects and confidence intervals are given. The empirical analysis of time series of bounded and unbounded counts reveals that the neural INGARCH models are able to outperform reasonable degenerate competitor models in terms of the information loss.