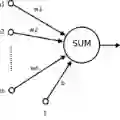
人工神经网络（Artificial Neural Network，即ANN），它从信息处理角度对人脑神经元网络进行抽象，建立某种简单模型，按不同的连接方式组成不同的网络。在工程与学术界也常直接简称为神经网络或类神经网络。神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数（activation function）。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。
精品内容
专知会员服务
3+阅读 · 2020年6月4日
专知会员服务
49+阅读 · 2020年3月31日
子主题
微信扫码咨询专知VIP会员