基于 Keras 用深度学习预测时间序列

作者：徐瑞龙，量化分析师

博客专栏：

https://www.cnblogs.com/xuruilong100

前文推送：

时间序列分析工具箱——timetk

时间序列预测一直以来是机器学习中的一个难题。

在本篇文章中，将介绍如何在 R 中使用 keras 深度学习包构建神经网络模型实现时间序列预测。

文章的主要内容：

• 如何将时间序列预测问题表示成为一个回归问题，并建立对应的神经网络模型。

• 如何使用滞后时间的数据实现时间序列预测，并建立对应的神经网络模型。

问题描述

“航班旅客数据”是一个常用的时间序列数据集，该数据包含了 1949 至 1960 年 12 年间的月度旅客数据，共有 144 个观测值。

下载链接：

international-airline-passengers.csv

多层感知机回归

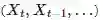
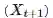
时间序列预测中最简单的思路之一便是寻找当前和过去数据与未来数据之间的关系，这种关系通常会表示成为一个回归问题。

下面着手将时间序列预测问题表示成一个回归问题，并建立神经网络模型用于预测。

首先，加载相关 R 包。

library(keras) library(dplyr) library(ggplot2) library(ggthemes) library(lubridate)

神经网络模型在训练时存在一定的随机性，所以要为计算统一随机数环境

set.seed(7)

画出整体数据的曲线图，对问题有一个直观的认识。

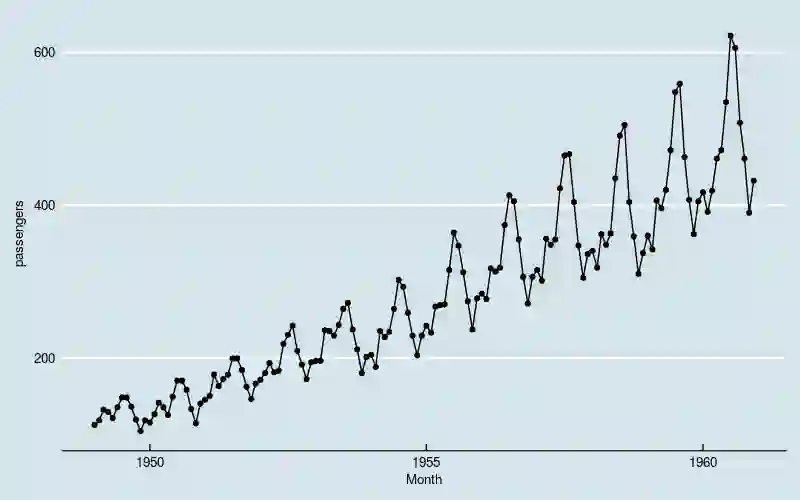
dataframe <- read.csv(    'international-airline-passengers.csv') dataframe$Month <- paste0(dataframe$Month,'-01') %>%    ymd() ggplot(    data = dataframe,    mapping = aes(        x = Month,        y = passengers)) +    geom_line() +    geom_point() +    theme_economist() +    scale_color_economist()

图1

很显然，数据体现出“季节性”，同时存在线性增长和波动水平增大的趋势。

将数据集分成两部分：训练集和测试集，比例分别占数据集的 2/3 和 1/3。

dataset <- dataframe$passengers train_size <- as.integer(length(dataset) * 0.67) test_size <- length(dataset) - train_size train <- dataset[1:train_size] test <- dataset[(train_size + 1):length(dataset)] cat(length(train), length(test))

96 48

为训练神经网络对数据做预处理，用数据构造出两个矩阵，分别是“历史数据”（作为预测因子）和“未来数据”（作为预测目标）。这里用最近一个月的历史数据做预测。

create_dataset <- function(dataset,                           look_back = 1) {    l <- length(dataset)    dataX <- matrix(nrow = l - look_back, ncol = look_back)    for (i in 1:ncol(dataX))    {        dataX[, i] <- dataset[i:(l - look_back + i - 1)]    }    dataY <- matrix(        data = dataset[(look_back + 1):l],        ncol = 1)    return(        list(            dataX = dataX,            dataY = dataY)) } look_back <- 1 trainXY <- create_dataset(train, look_back) testXY <-  create_dataset(test, look_back)

下面构造神经网络的框架结构并用处理过的训练数据训练。

model <- keras_model_sequential() model %>%    layer_dense(        units = 8,        input_shape = c(look_back),        activation = 'relu') %>%    layer_dense(units = 1) %>%    compile(        loss = 'mean_squared_error',        optimizer = 'adam') %>%    fit(        trainXY$dataX,        trainXY$dataY,        epochs = 200,        batch_size = 2,        verbose = 2)

训练结果如下。

trainScore <- model %>%    evaluate(        trainXY$dataX,        trainXY$dataY,        verbose = 0) testScore <- model %>%    evaluate(        testXY$dataX,        testXY$dataY,        verbose = 0) sprintf(    'Train Score: %.2f MSE (%.2f RMSE)',    trainScore,    sqrt(trainScore)) sprintf(    'Test Score: %.2f MSE (%.2f RMSE)',    testScore,    sqrt(testScore))

[1] "Train Score: 538.50 MSE (23.21 RMSE)"[1] "Test Score: 2342.33 MSE (48.40 RMSE)

把训练数据的拟合值、测试数据的预测值和原始数据画在一起。

trainPredict <- model %>%    predict(trainXY$dataX) testPredict <- model %>%    predict(testXY$dataX) df <- data.frame(    index = 1:length(dataset),    value = dataset,    type = 'raw') %>%    rbind(        data.frame(            index = 1:length(trainPredict) + look_back,            value = trainPredict,            type = 'train')) %>%    rbind(        data.frame(            index = 1:length(testPredict) + look_back + length(train),            value = testPredict,            type = 'test')) ggplot(data = df) +    geom_line(        mapping = aes(            x = index,            y = value,            color = type)) +    geom_point(        mapping = aes(            x = index,            y = value,            color = type)) +    geom_vline(        xintercept = length(train) + 0.5) +    theme_economist() +    scale_color_economist()

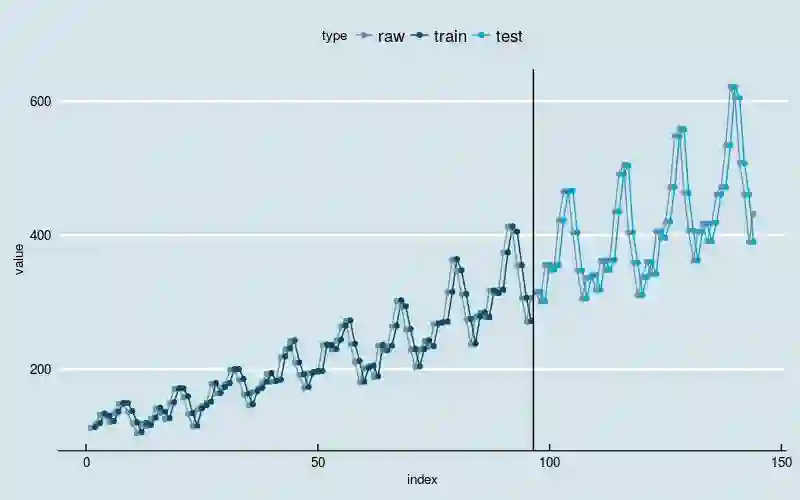
图2

黑线左边是训练部分，右边是测试部分。

从图中可以看出，神经网络模型抓住了数据线性增长和波动率逐渐增加的两大趋势，在不做数据转换的前提下，这是经典的时间序列分析模型不容易做到的；但是很可能没有识别出“季节性”的结构特点，因为训练和预测结果和原始数据之间存在“平移错位”。

多层感知机回归结合“窗口法”

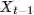
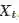
前面的例子可以看出，如果仅使用来预测，很难让神经网络模型识别出“季节性”的结构特征，因此有必要尝试增加“窗口”宽度，使用更多的历史数据（包含一个完整的周期）训练模型。

下面将数 create_dataset 中的参数 look_back 设置为 12，用来包含过去 1 年的历史数据，重新训练模型。

look_back <- 12 trainXY <- create_dataset(train, look_back) testXY <-  create_dataset(test, look_back) model <- keras_model_sequential() model %>%    layer_dense(        units = 8,        input_shape = c(look_back),        activation = 'relu') %>%    layer_dense(units = 1) %>%    compile(        loss = 'mean_squared_error',        optimizer = 'adam') %>%    fit(        trainXY$dataX,        trainXY$dataY,        epochs = 200,        batch_size = 2,        verbose = 2) trainScore <- model %>%    evaluate(        trainXY$dataX,        trainXY$dataY,        verbose = 0) testScore <- model %>%    evaluate(        testXY$dataX,        testXY$dataY,        verbose = 0) sprintf(    'Train Score: %.2f MSE (%.2f RMSE)',    trainScore,    sqrt(trainScore)) sprintf(    'Test Score: %.2f MSE (%.2f RMSE)',    testScore,    sqrt(testScore)) trainPredict <- model %>%    predict(trainXY$dataX) testPredict <- model %>%    predict(testXY$dataX) df <- data.frame(    index = 1:length(dataset),    value = dataset,    type = 'raw') %>%    rbind(        data.frame(            index = 1:length(trainPredict) + look_back,            value = trainPredict,            type = 'train')) %>%    rbind(        data.frame(            index = 1:length(testPredict) + look_back + length(train),            value = testPredict,            type = 'test')) ggplot(data = df) +    geom_line(        mapping = aes(            x = index,            y = value,            color = type)) +    geom_point(        mapping = aes(            x = index,            y = value,            color = type)) +    geom_vline(        xintercept = length(train) + 0.5) +    theme_economist() +    scale_color_economist()

[1] "Train Score: 157.17 MSE (12.54 RMSE)" [1] "Test Score: 690.69 MSE (26.28 RMSE)"

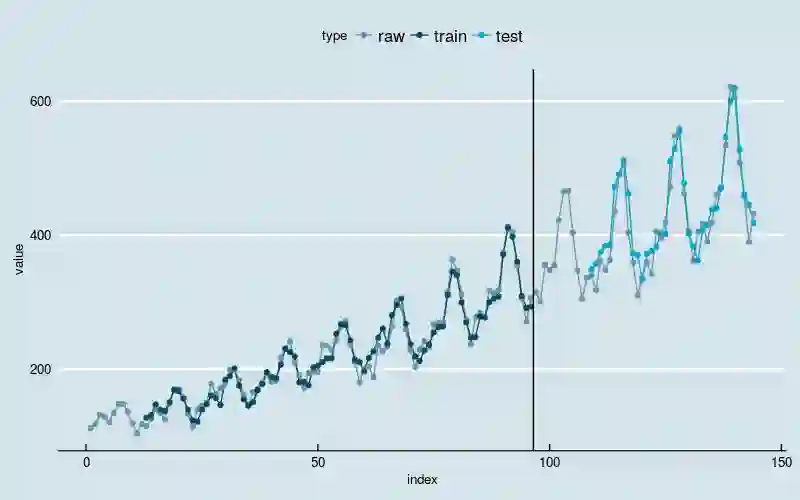
图3

新的模型基本上克服了“平移错位”的现象，同时依然能够识别出线性增长和波动率逐渐增加的两大趋势。

改进方向

• 目前对“季节性”的识别是靠增加历史数据实现的，能否从神经网络结构的方向入手。

• 目前的模型中几乎没有用到“特征工程”，如何用特征工程表示数据中存在的主要趋势和结构化特征。

• DNN + ARIMA：一方作为另外一方的“特征工程”手段。

扩展阅读

• 《神经网络与深度学习》

• keras on MRAN

大家都在看

2017年R语言发展报告（国内）

精心整理 | R语言中文社区历史文章合集（作者篇）

精心整理 | R语言中文社区历史文章整理（类型篇）

公众号后台回复关键字即可学习

回复 爬虫            爬虫三大案例实战  
回复 Python       1小时破冰入门

回复 数据挖掘     R语言入门及数据挖掘
回复 人工智能     三个月入门人工智能
回复 数据分析师  数据分析师成长之路 
回复 机器学习      机器学习的商业应用
回复 数据科学      数据科学实战
回复 常用算法      常用数据挖掘算法