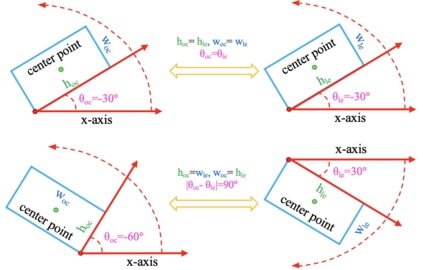
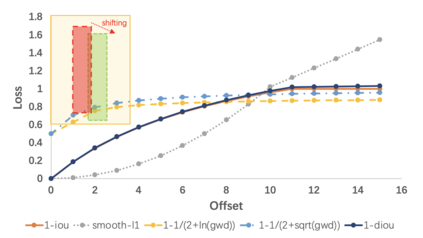
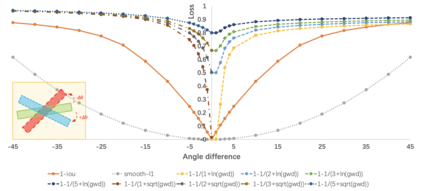
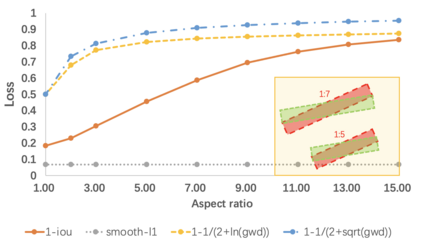
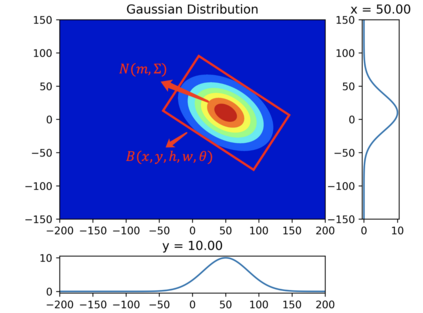
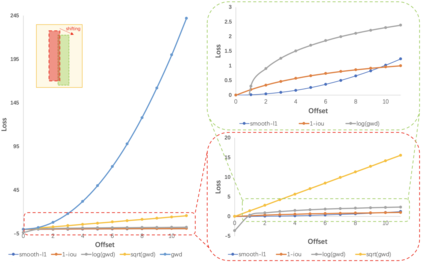
Boundary discontinuity and its inconsistency to the final detection metric have been the bottleneck for rotating detection regression loss design. In this paper, we propose a novel regression loss based on Gaussian Wasserstein distance as a fundamental approach to solve the problem. Specifically, the rotated bounding box is converted to a 2-D Gaussian distribution, which enables to approximate the indifferentiable rotational IoU induced loss by the Gaussian Wasserstein distance (GWD) which can be learned efficiently by gradient back-propagation. GWD can still be informative for learning even there is no overlapping between two rotating bounding boxes which is often the case for small object detection. Thanks to its three unique properties, GWD can also elegantly solve the boundary discontinuity and square-like problem regardless how the bounding box is defined. Experiments on five datasets using different detectors show the effectiveness of our approach. Codes are available at https://github.com/yangxue0827/RotationDetection.
翻译:边界的不连续性及其与最后探测指标的不一致性一直是旋转探测回归损失设计的瓶颈。 在本文中,我们提出基于高斯扬·瓦西斯坦距离的新的回归损失,作为解决问题的基本方法。具体地说,旋转的捆绑框转换成2-D高斯分布,使高斯登·瓦西尔斯坦距离(GWD)的无差别旋转IoU引起的损失能够近似于无差别的旋转 IoU 损失,而这种损失可以通过梯度回传有效学习。 GWD 仍然可以提供信息,学习两个旋转捆绑盒之间没有重叠之处,而这往往是小天体探测的情况。由于它的三个独特的特性,GWD还可以优雅地解决边界不连续和方形问题,而不论捆绑框是如何界定的。 使用不同探测器对五个数据集的实验显示了我们的方法的有效性。 代码可以在 https://github.com/yangxue0827/Rotation Contagition上查阅。