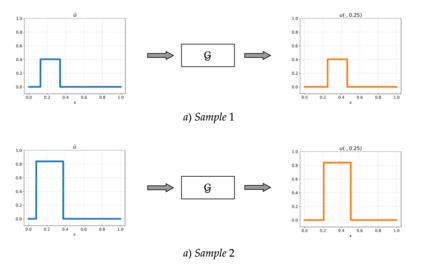
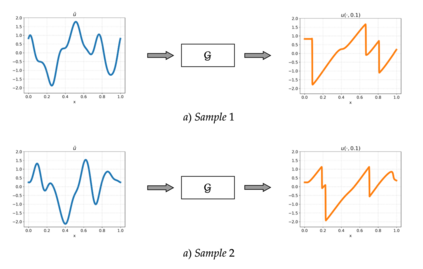
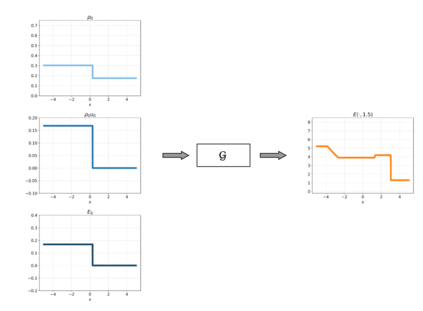
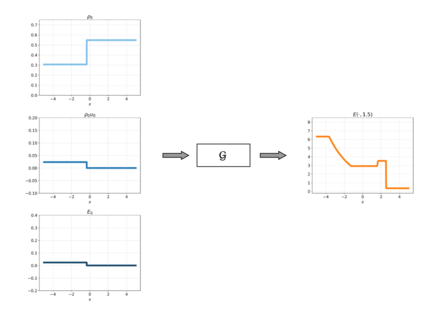
A large class of hyperbolic and advection-dominated PDEs can have solutions with discontinuities. This paper investigates, both theoretically and empirically, the operator learning of PDEs with discontinuous solutions. We rigorously prove, in terms of lower approximation bounds, that methods which entail a linear reconstruction step (e.g. DeepONet or PCA-Net) fail to efficiently approximate the solution operator of such PDEs. In contrast, we show that certain methods employing a non-linear reconstruction mechanism can overcome these fundamental lower bounds and approximate the underlying operator efficiently. The latter class includes Fourier Neural Operators and a novel extension of DeepONet termed shift-DeepONet. Our theoretical findings are confirmed by empirical results for advection equation, inviscid Burgers' equation and compressible Euler equations of aerodynamics.
翻译:大量双曲和对冲占主导地位的PDE可以有不连续的解决方案。 本文从理论上和经验上调查了操作者以不连续的解决方案学习PDE的操作者。 我们严格地从较低的近似界限方面证明,需要采取线性重建步骤的方法( 如DeepONet 或 PAC-Net ) 无法有效地接近这种PDE 的解决方案操作者。 相反, 我们表明, 使用非线性重建机制的某些方法可以克服这些基本的下限并有效地接近基本操作者。 后一类方法包括 Fourier Neural 操作员和DeepONet 的新型扩展, 称为 Shift- DeepONet 。 我们的理论结论得到下列实验结果的证实: 适应方程式、 隐形 Burgerers 的方程式和 空气动力学的可兼容性 Euler 方程式。