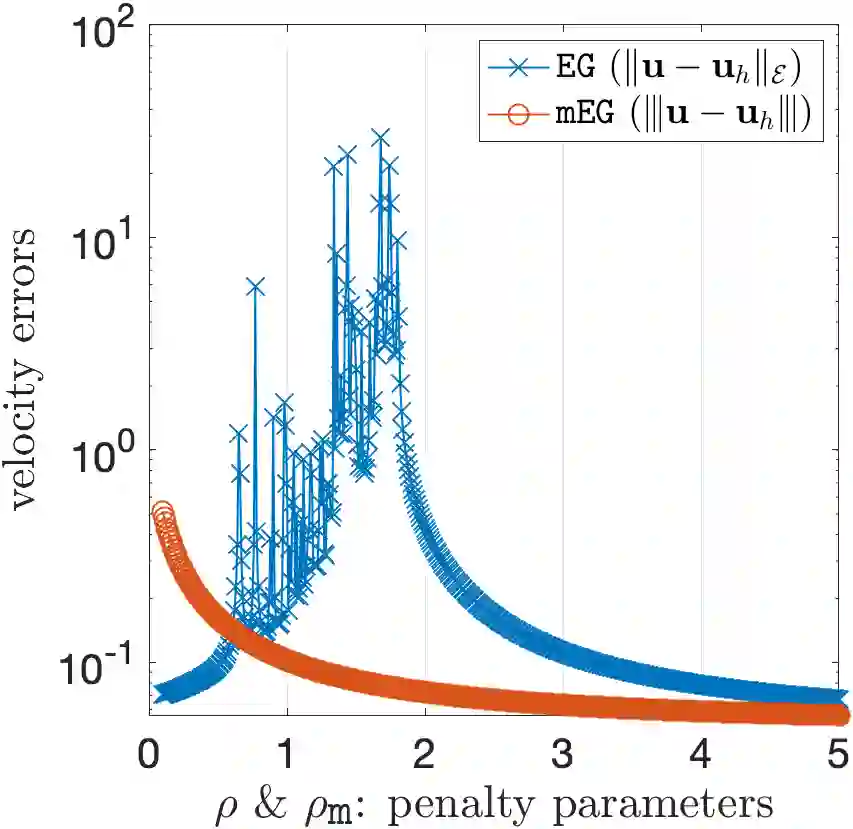
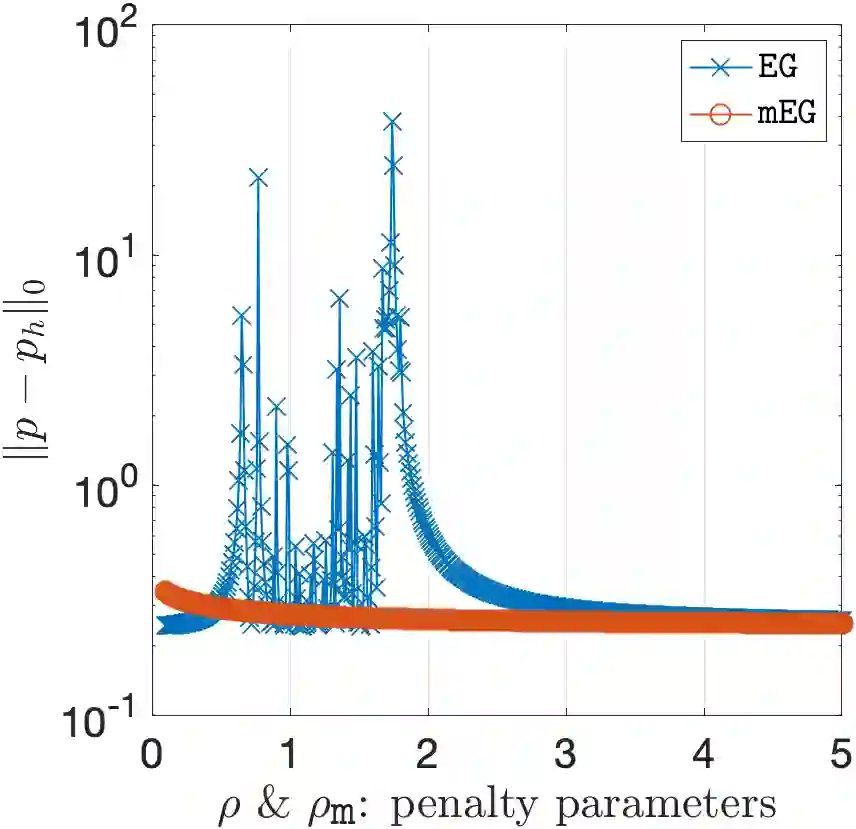
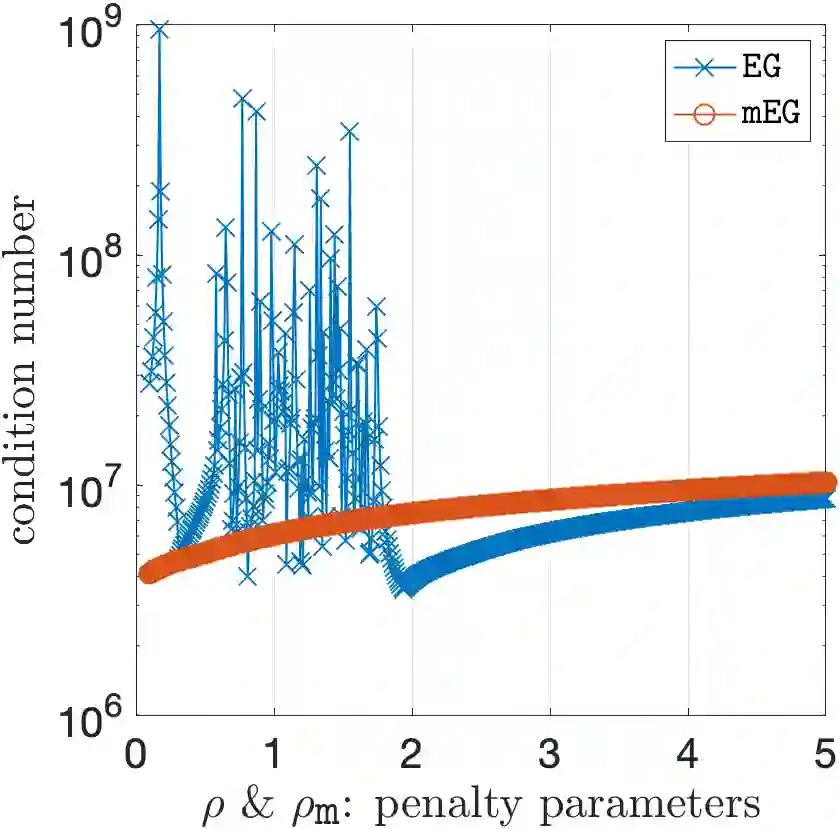
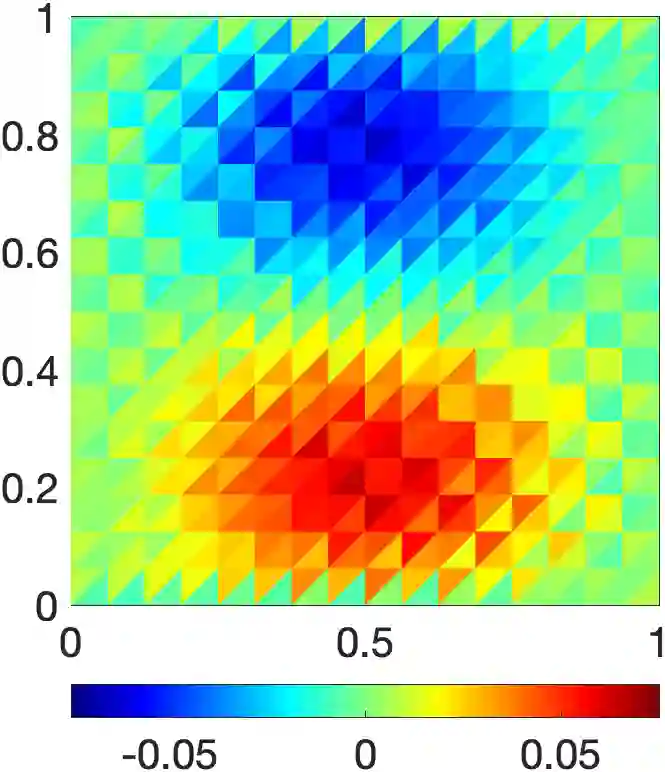
In this paper, we propose a low-cost, parameter-free, and pressure-robust Stokes solver based on the enriched Galerkin (EG) method with a discontinuous velocity enrichment function. The EG method employs the interior penalty discontinuous Galerkin (IPDG) formulation to weakly impose the continuity of the velocity function. However, the symmetric IPDG formulation, despite of its advantage of symmetry, requires a lot of computational effort to choose an optimal penalty parameter and to compute different trace terms. In order to reduce such effort, we replace the derivatives of the velocity function with its weak derivatives computed by the geometric data of elements. Therefore, our modified EG (mEG) method is a parameter-free numerical scheme which has reduced computational complexity as well as optimal rates of convergence. Moreover, we achieve pressure-robustness for the mEG method by employing a velocity reconstruction operator on the load vector on the right-hand side of the discrete system. The theoretical results are confirmed through numerical experiments with two- and three-dimensional examples.
翻译:在本文中,我们基于浓缩的Galerkin (EG) 方法提出一个低成本、无参数和压力-气旋Stokes 求解器,该方法基于浓缩的Galerkin (EG) 方法,具有不连续速度浓缩功能。EG 方法使用内部惩罚不连续的Galerkin (IPDG) 配方来弱化速度函数的连续性。然而,尽管对称 IPDG 配方具有对称的优势,但需要大量计算努力来选择最佳刑罚参数和计算不同的跟踪术语。为了减少这种努力,我们用其微弱衍生物替换速度函数的衍生物,而根据元素的几何数据计算。因此,我们修改后的EGEG (MEG) 方法是一种无参数的数字方法,它减少了计算复杂性,并且是最佳的趋同率。此外,我们通过在离散系统右侧的负载矢量矢量器上使用速度重建操作器,从而实现对 mEGG方法的压力- 的压- 。通过二维和三维实例的数字实验证实了理论结果。