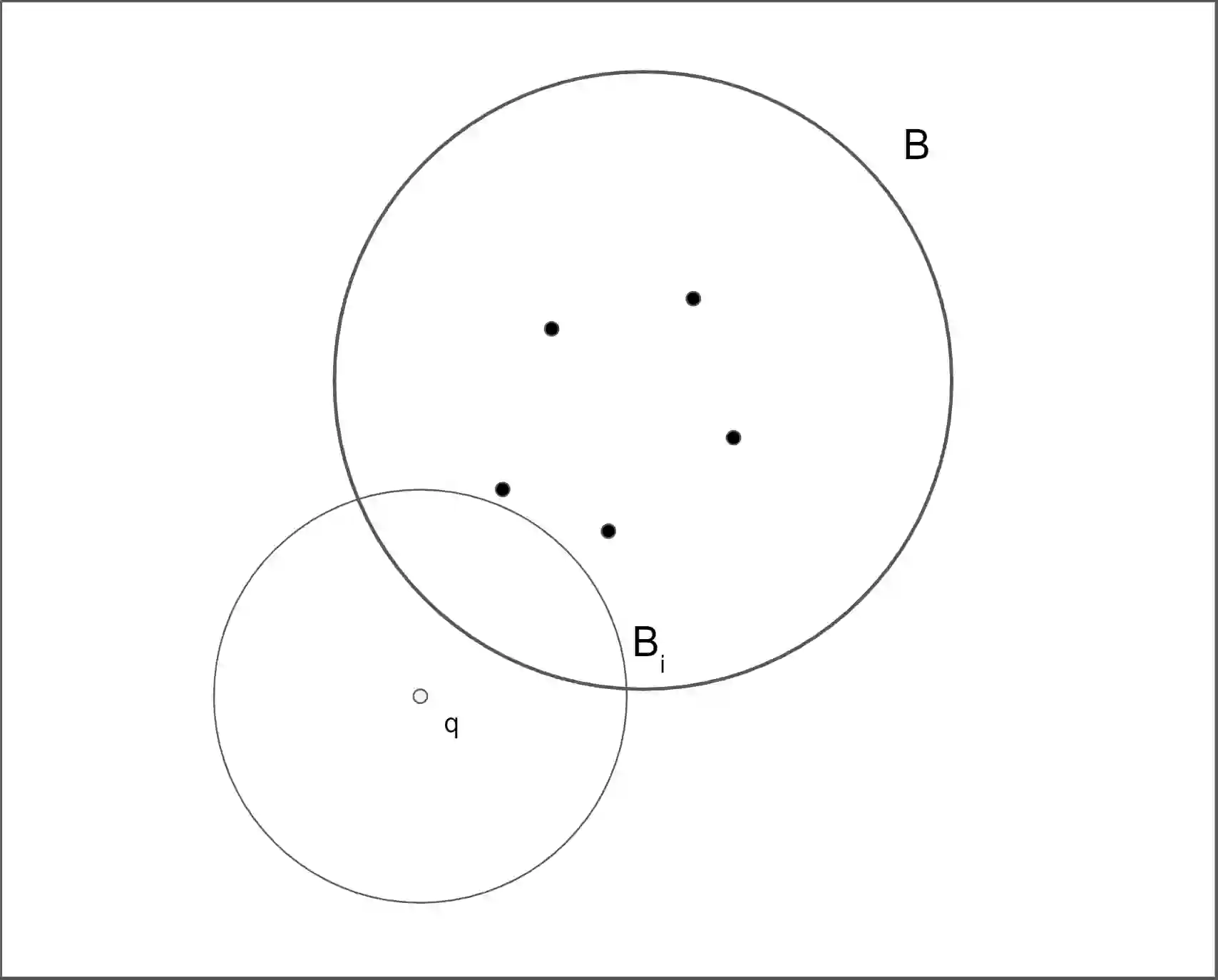
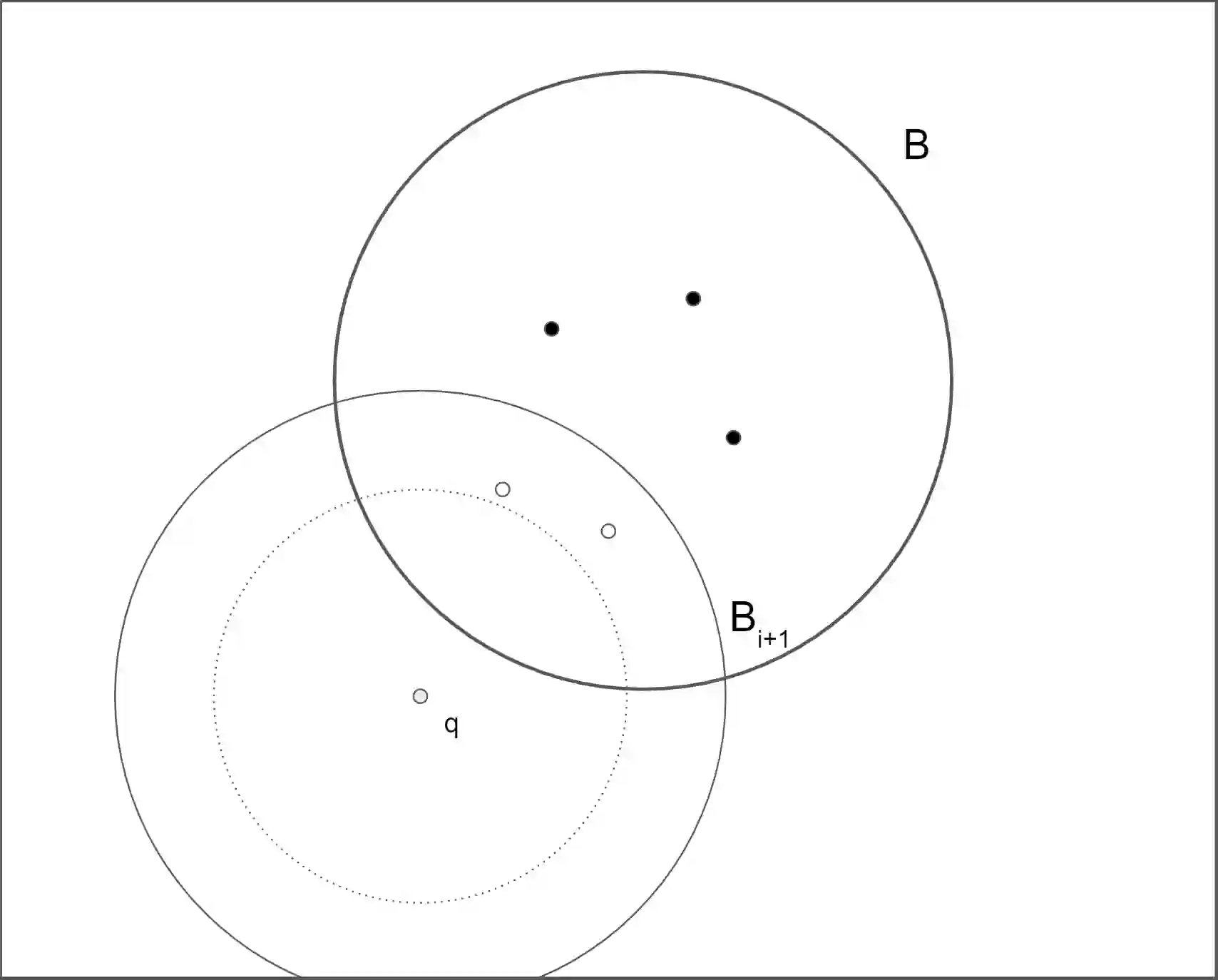
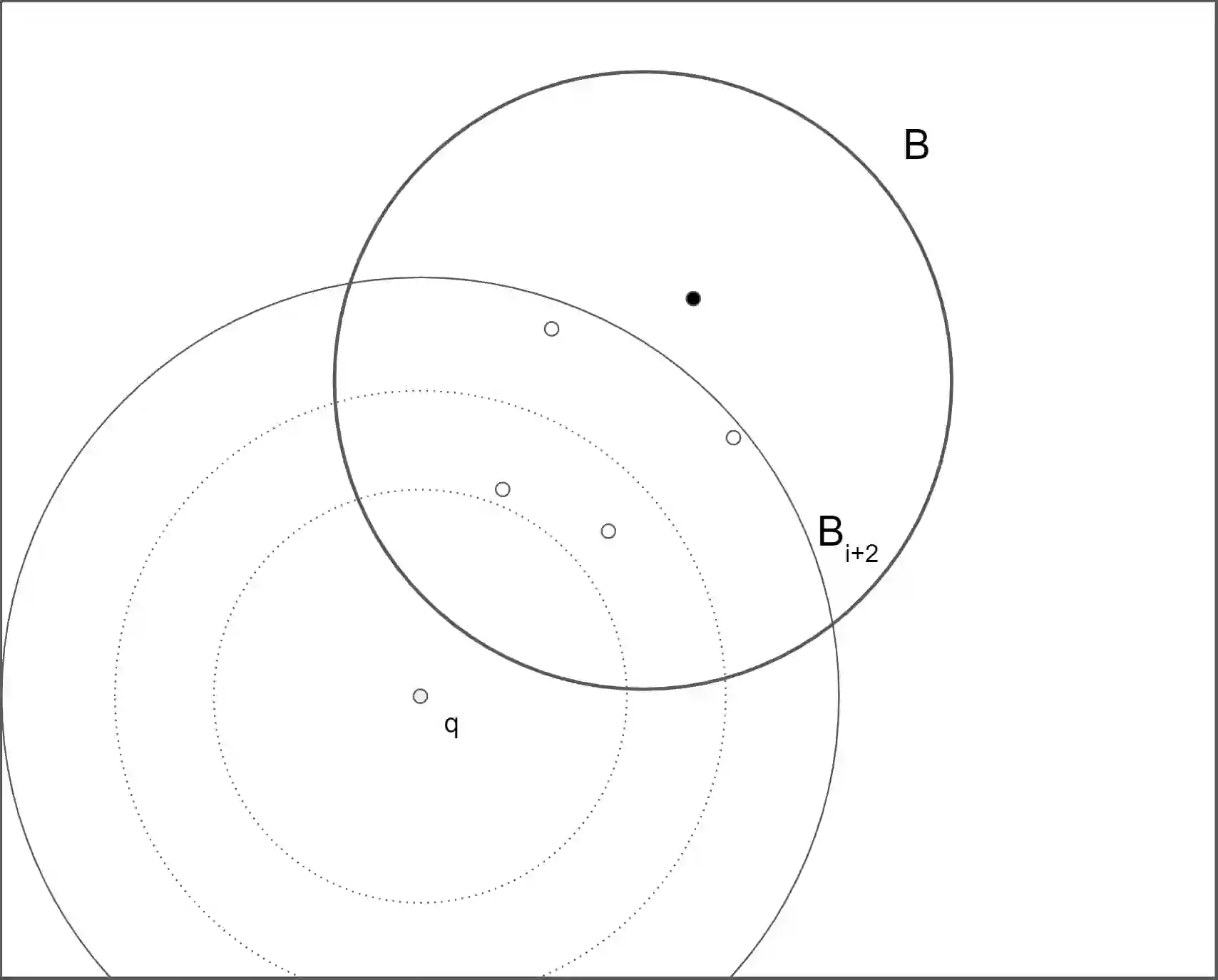
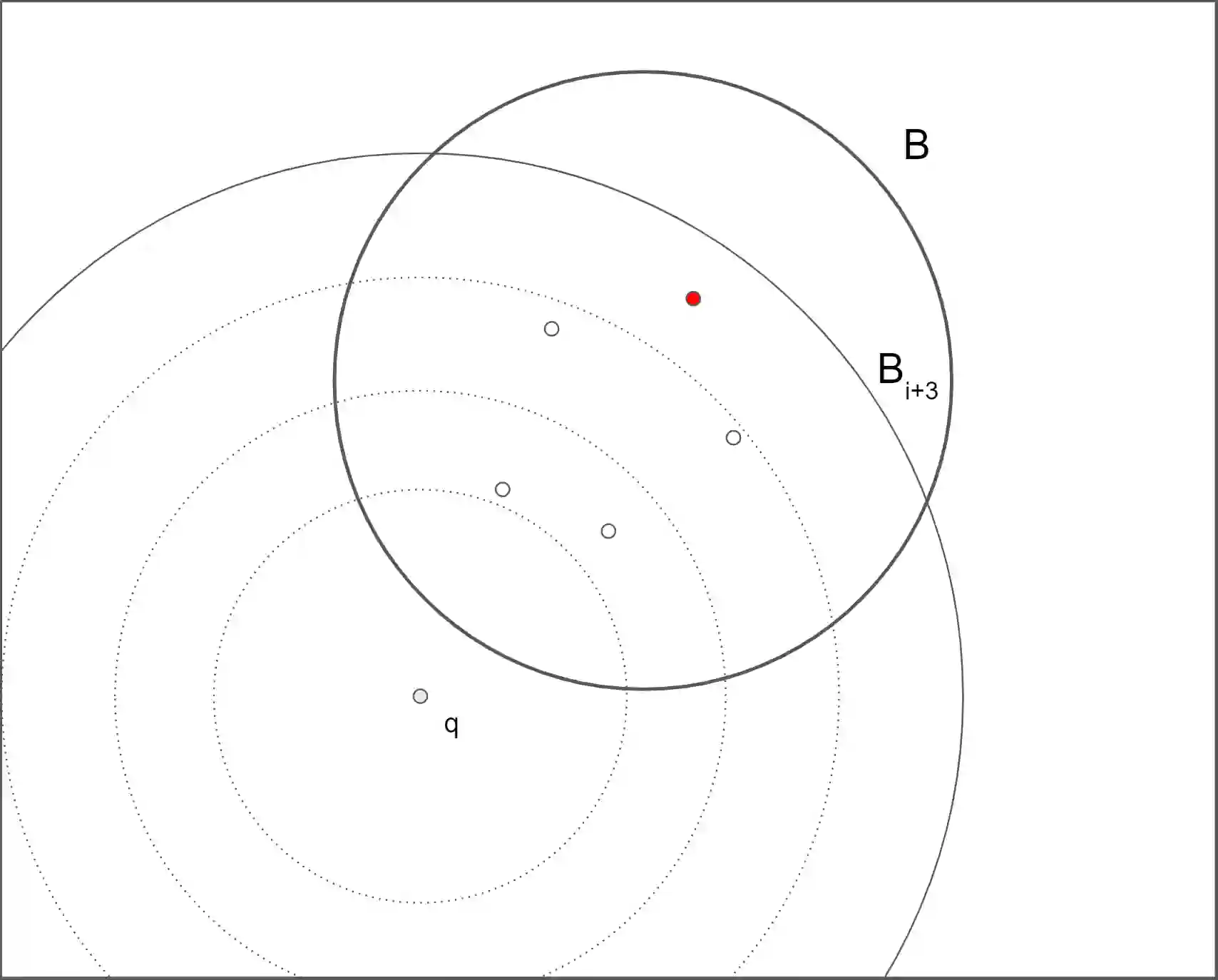
Range-aggregate query is an important type of queries with numerous applications. It aims to obtain some structural information (defined by an aggregate function $F(\cdot)$) of the points (from a point set $P$) inside a given query range $B$. In this paper, we study the range-aggregate query problem in high dimensional space for two aggregate functions: (1) $F(P \cap B)$ is the farthest point in $P \cap B$ to a query point $q$ in $\mathbb{R}^d$ and (2) $F(P \cap B)$ is the minimum enclosing ball (MEB) of $P \cap B$. For problem (1), called In-Range Farthest Point (IFP) Query, we develop a bi-criteria approximation scheme: For any $\epsilon>0$ that specifies the approximation ratio of the farthest distance and any $\gamma>0$ that measures the "fuzziness" of the query range, we show that it is possible to pre-process $P$ into a data structure of size $\tilde{O}_{\epsilon,\gamma}(dn^{1+\rho})$ in $\tilde{O}_{\epsilon,\gamma}(dn^{1+\rho})$ time such that given any $\mathbb{R}^d$ query ball $B$ and query point $q$, it outputs in $\tilde{O}_{\epsilon,\gamma}(dn^{\rho})$ time a point $p$ that is a $(1-\epsilon)$-approximation of the farthest point to $q$ among all points lying in a $(1+\gamma)$-expansion $B(1+\gamma)$ of $B$, where $0<\rho<1$ is a constant depending on $\epsilon$ and $\gamma$ and the hidden constants in big-O notations depend only on $\epsilon$, $\gamma$ and $\text{Polylog}(nd)$. For problem (2), we show that the IFP result can be applied to develop query scheme with similar time and space complexities to achieve a $(1+\epsilon)$-approximation for MEB.
翻译:网格查询是一种重要的查询类型 。 它旨在获取某种结构信息( 由一个总函数 $F (cdot) $, 美元 美元) 。 在给定查询范围内, $B$ 。 在本文中, 我们研究高维空间中两种总计函数的网格查询问题:(1) $F (P\ cap B) 最远的点是 $B$, 至一个查询点$, $mathbb 美元 ; $F (P\cd) 最远的点是 $ $ 美元 。 $F( 美元) 最低的网格 $ 。 对于问题(1), 我们研究高维域域域域的网格查询问题: $(epl) 0. 0 确定远端距离的近似比值, 任何美元=gammam 美元, 在查询范围内的“ fouzzn $ 美元 ”, 我们显示它有可能是预处理 美元 美元 。