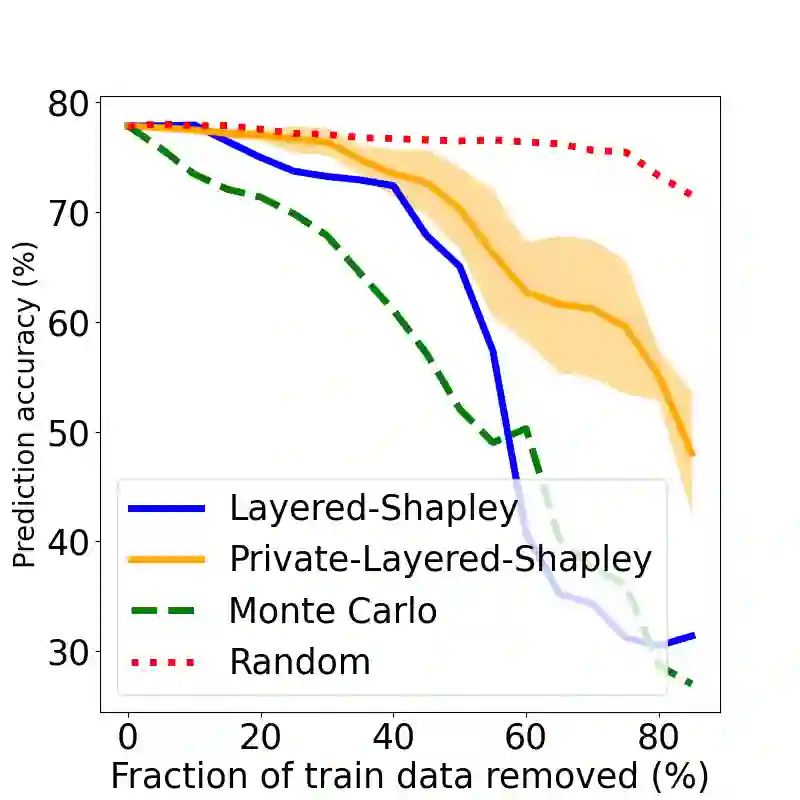
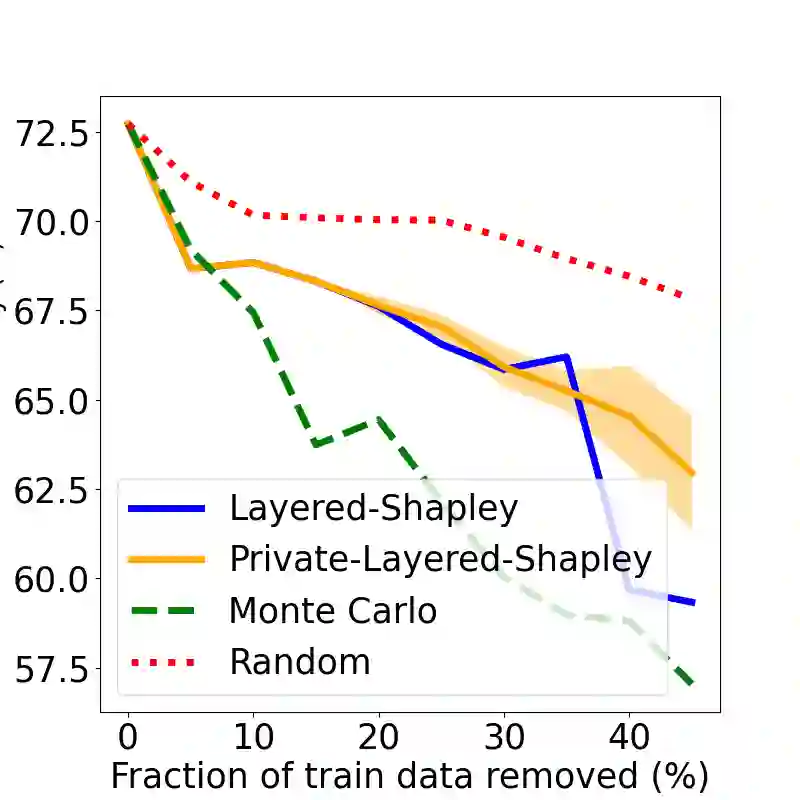
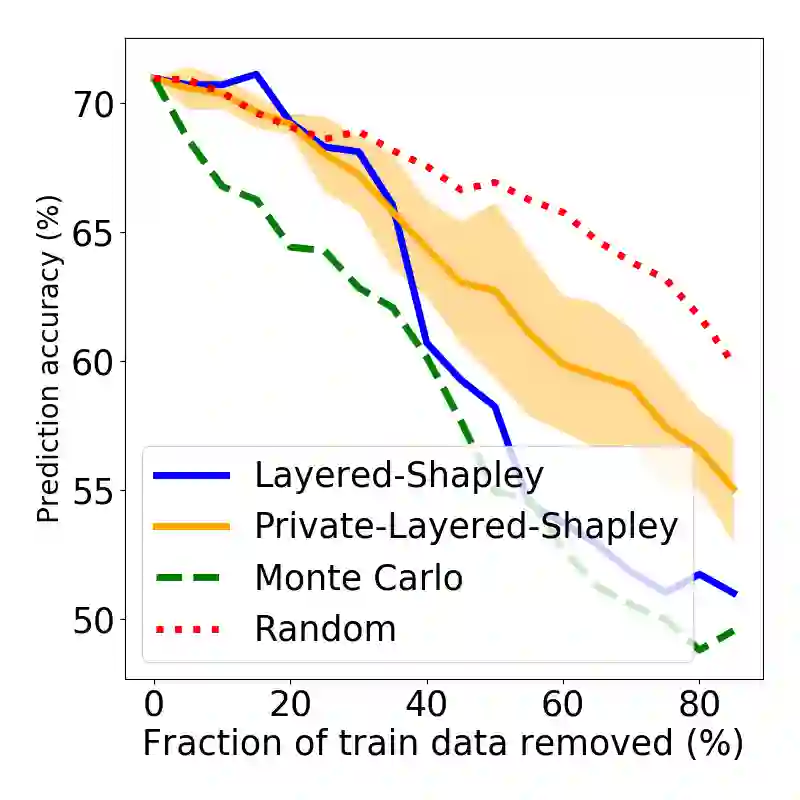
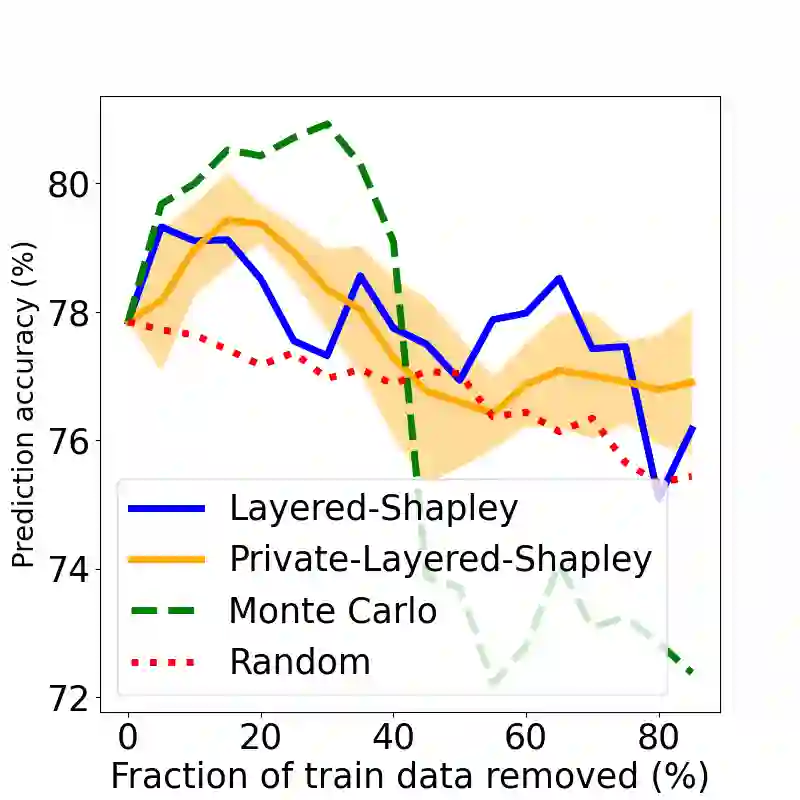
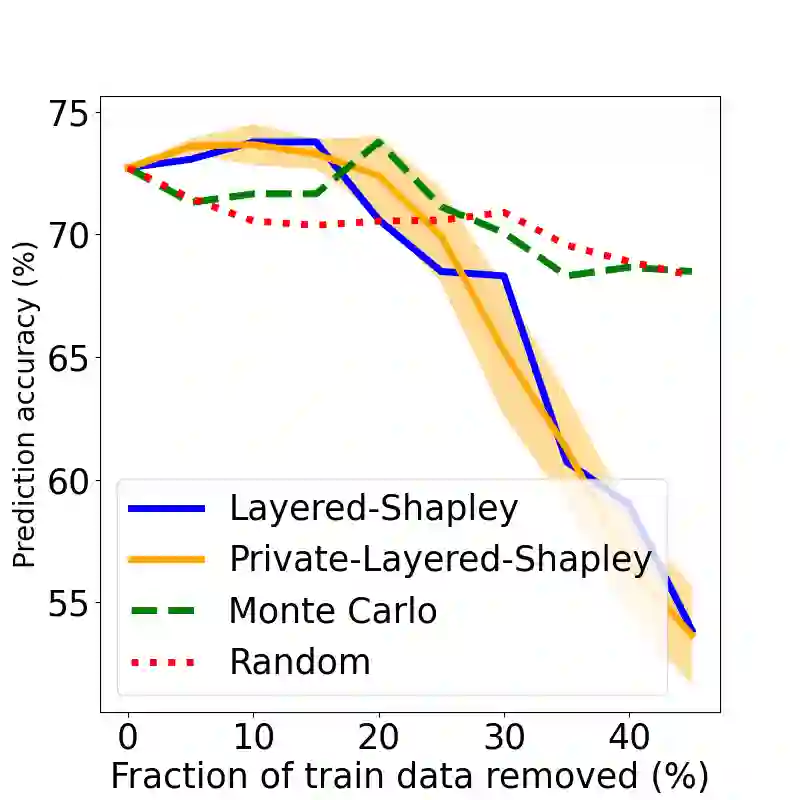
The Shapley value has been proposed as a solution to many applications in machine learning, including for equitable valuation of data. Shapley values are computationally expensive and involve the entire dataset. The query for a point's Shapley value can also compromise the statistical privacy of other data points. We observe that in machine learning problems such as empirical risk minimization, and in many learning algorithms (such as those with uniform stability), a diminishing returns property holds, where marginal benefit per data point decreases rapidly with data sample size. Based on this property, we propose a new stratified approximation method called the Layered Shapley Algorithm. We prove that this method operates on small (O(\polylog(n))) random samples of data and small sized ($O(\log n)$) coalitions to achieve the results with guaranteed probabilistic accuracy, and can be modified to incorporate differential privacy. Experimental results show that the algorithm correctly identifies high-value data points that improve validation accuracy, and that the differentially private evaluations preserve approximate ranking of data.
翻译:作为机器学习中许多应用,包括数据公平估值的解决方案,提出了沙普利值,作为机器学习中许多应用的解决方案。沙普利值计算成本昂贵,涉及整个数据集。点的沙普利值查询也可能损害其他数据点的统计隐私性。我们发现,在诸如尽量减少实验风险等机器学习问题和许多学习算法(如具有统一稳定性的算法)中,回报率不断下降,数据点的边际效益随数据样本大小而迅速下降。基于此属性,我们提出了一种新的分层近似法,称为“层沙普利阿尔戈里特姆 ” 。我们证明,这一方法以小型(O(polylog(n)))随机抽样数据和小规模(O(log n)美元)联盟的方式运作,以保证概率准确性的方式实现结果,并可以修改以纳入差异隐私。实验结果显示,该算法正确地确定了提高验证准确度的高价值数据点,而差异私人评价保留了数据的近似排序。