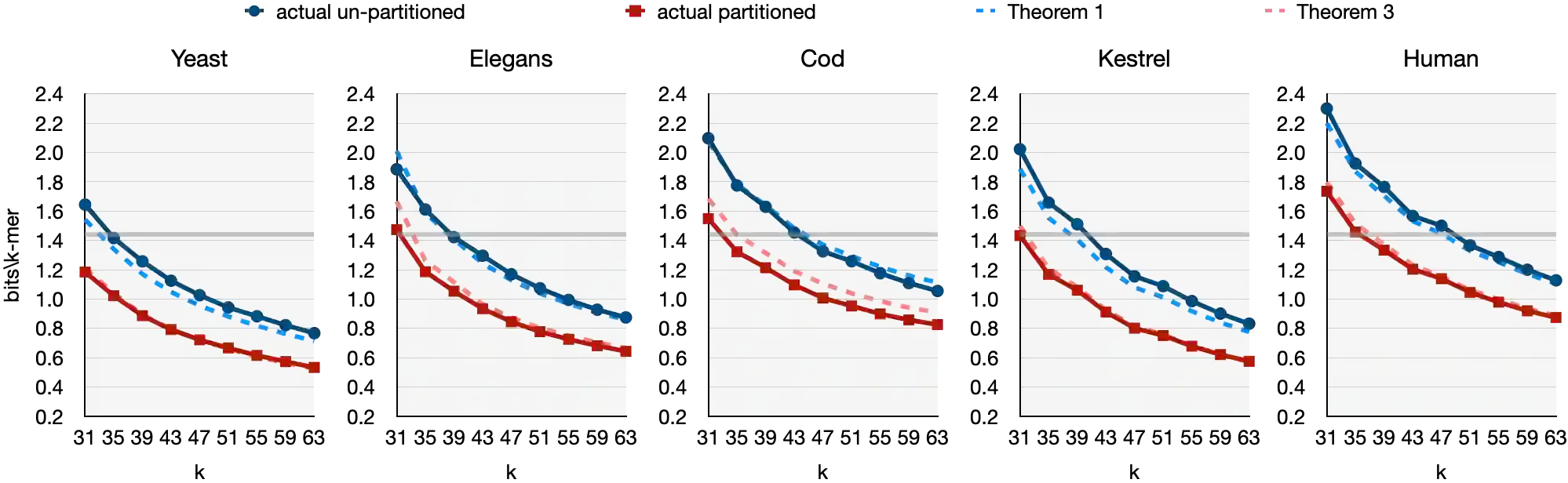
Minimal perfect hashing is the problem of mapping a static set of $n$ distinct keys into the address space $\{1,\ldots,n\}$ bijectively. It is well-known that $n\log_2(e)$ bits are necessary to specify a minimal perfect hash function (MPHF) $f$, when no additional knowledge of the input keys is to be used. However, it is often the case in practice that the input keys have intrinsic relationships that we can exploit to lower the bit complexity of $f$. For example, consider a string and the set of all its distinct $k$-mers as input keys: since two consecutive $k$-mers share an overlap of $k-1$ symbols, it seems possible to beat the classic $\log_2(e)$ bits/key barrier in this case. Moreover, we would like $f$ to map consecutive $k$-mers to consecutive addresses, as to also preserve as much as possible their relationship in the codomain. This is a useful feature in practice as it guarantees a certain degree of locality of reference for $f$, resulting in a better evaluation time when querying consecutive $k$-mers. Motivated by these premises, we initiate the study of a new type of locality-preserving MPHF designed for $k$-mers extracted consecutively from a collection of strings. We design a construction whose space usage decreases for growing $k$ and discuss experiments with a practical implementation of the method: in practice, the functions built with our method can be several times smaller and even faster to query than the most efficient MPHFs in the literature.
翻译:极小完美哈希的问题是将一个由 $n$ 个不同键组成的静态集合映射到地址空间 $\{1,\ldots,n\}$ 上,使映射是双射。众所周知,当不使用额外的输入键信息时,需要 $n\log_2(e)$ 位来指定极小完美哈希函数(MPHF)$f$。然而,在实践中,输入的键通常具有我们可以利用的内在关系,以降低 $f$ 的二进制复杂度。例如,考虑字符串及其所有不同 $k$-mer 的集合作为输入键的情况:由于两个连续的 $k$-mer 共享 $k-1$ 个符号的重叠,因此在这种情况下似乎可以打破经典的 $\log_2(e)$ bits/key 的限制。此外,我们希望 $f$ 将相邻的 $k$-mer 映射到连续的地址,以在定义域中尽可能地保留它们的关系。这是一个实用的特征,因为它保证了 $f$ 的某种局部性质,从而在查询相邻的 $k$-mer 时导致更好的评估时间。受这些前提的启发,我们开始研究一种新类型的局部保持 MPHF,用于从一个字符串集合中连续提取 $k$-mer。我们设计了一种构造,其空间使用在 $k$ 增长时会减少,并讨论了一个实际实现方法的实验:实际上,我们构建的函数可以比文献中最有效的 MPHFs (Minimal Perfect Hash Function) 还要小好几倍,甚至查询速度更快。