k-稀疏恢复限制等距常数上界及压缩感知算法研究

项目名称： k-稀疏恢复限制等距常数上界及压缩感知算法研究

项目编号： No.61272028

项目类型： 面上项目

立项/批准年度： 2013

项目学科： 自动化技术、计算机技术

项目作者： 岑翼刚

作者单位： 北京交通大学

项目金额： 60万元

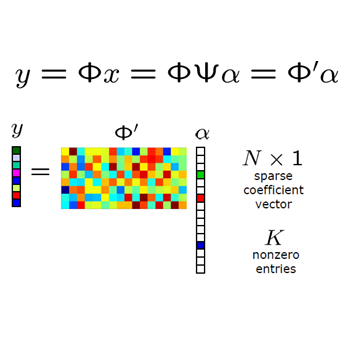
中文摘要： 压缩感知(CS)的目标是以较少的测量数据实现高维信号的恢复，是信息科学全新的理论。 (l1)约束极小化能准确或以很小的误差重构稀疏信号，只要测量矩阵的RIP常数满足一定的上界条件。然而，直接验证一个感知矩阵的RIP是困难的。为避免直接验证RIP，一个普遍的技巧是去表明随机生成的感知矩阵高概率地满足RIP。因此，RIP常数新界的研究一直是CS的一个热点。另外，实际信号的非稀疏性也制约了CS对信号的重构质量。本课题以感知矩阵的零空间为切入点，提出了研究RIP常数上界的统一方案，为获取RIP常数新界提供了一条新的途径。进一步，考虑了CS恢复算法与稀疏表示的相关性，通过研究峰值变换和小波树的特性，建立起信号稀疏表示和CS非线性重构的新算法，从而提高CS的算法性能和重构质量，为扩大CS的实际应用提供新的理论依据。

中文关键词： 压缩感知；限制等距常数新界；稀疏表示；稀疏恢复；低秩矩阵重构

英文摘要： The goal of Compressive Sensing(CS) is to recover the high-dimensional signals from a very limited number of measurements. It is a brand new theory in information science. (l1)-minimization can reconstruct sparse signals with a small or zero error provided that the RIP constants of the sensing matrices satisfy a certain bound. However, it is difficult to verify the RIP for a given sensing matrix. A general technique for avoiding verifying the RIP directly is to show that the randomly generating sensing matrix satisfis RIP with high probability. Hence, the study of the new bounds for the RIP constants is always a hot issue of CS. Moreover, the non-sparsity of practical signals also confine the quality of the recovered signals obtained by CS theory. Based on the null space of the sensing matrix, a unified approach for studying the upper bounds of RIP constants is proposed, which will provide a new way for capturing the new bounds of RIP constants. Further, the correlation between the CS algorithm and the sparse representation method is exploited. By investigating the natures of the peak transform and tree structure of the wavelet coefficients, new algorithms for the sparse representation and CS non-linear reconstruction of practical signals are established, which can improve the performance of CS algorithms and t

英文关键词： Compressed Sensing；New bounds of restricted isometry constants；Sparse representation；Sparse recovery；Low-rank matrix reconstruction