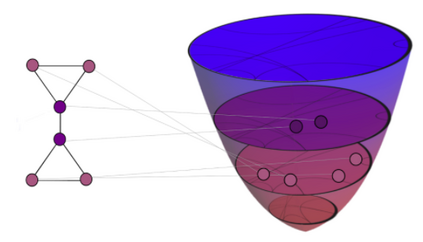
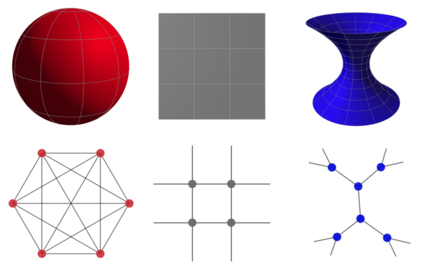
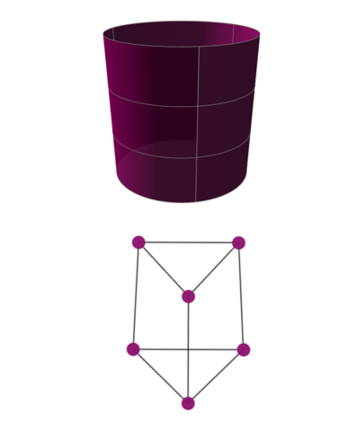
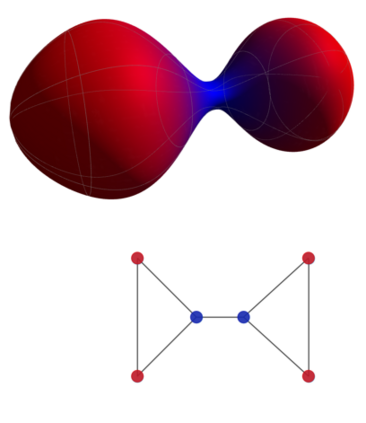
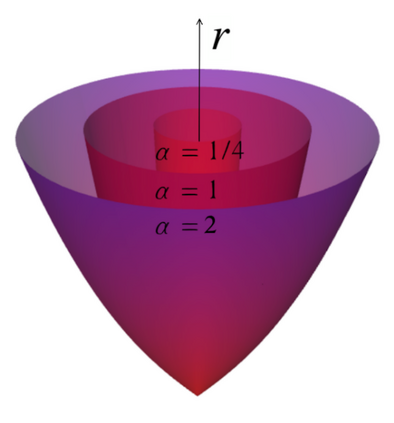
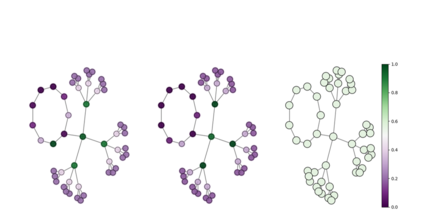
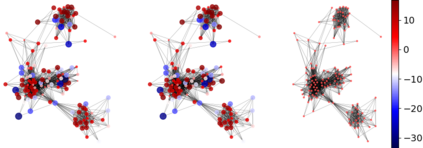
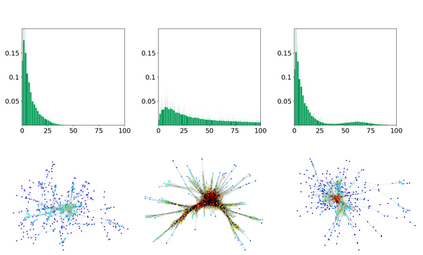
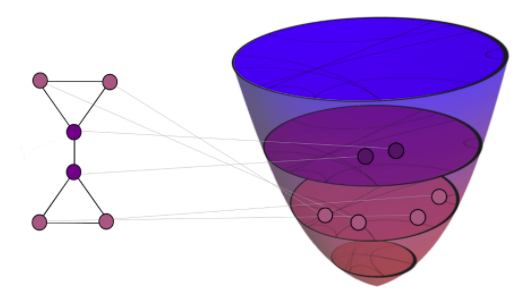
Graph embeddings, wherein the nodes of the graph are represented by points in a continuous space, are used in a broad range of Graph ML applications. The quality of such embeddings crucially depends on whether the geometry of the space matches that of the graph. Euclidean spaces are often a poor choice for many types of real-world graphs, where hierarchical structure and a power-law degree distribution are linked to negative curvature. In this regard, it has recently been shown that hyperbolic spaces and more general manifolds, such as products of constant-curvature spaces and matrix manifolds, are advantageous to approximately match nodes pairwise distances. However, all these classes of manifolds are homogeneous, implying that the curvature distribution is the same at each point, making them unsuited to match the local curvature (and related structural properties) of the graph. In this paper, we study graph embeddings in a broader class of heterogeneous rotationally-symmetric manifolds. By adding a single extra radial dimension to any given existing homogeneous model, we can both account for heterogeneous curvature distributions on graphs and pairwise distances. We evaluate our approach on reconstruction tasks on synthetic and real datasets and show its potential in better preservation of high-order structures and heterogeneous random graphs generation.
翻译:图形嵌入图 嵌入图, 图形的节点由连续空间的点表示, 用于 图表 ML 应用的广泛范围。 这种嵌入的质量关键地取决于空间的几何与图形的距离是否一致。 ELCLidean 空格对于许多类型的真实世界图形来说, 其等级结构和电法度分布与负曲线相关, 通常选择不善。 在这方面, 最近显示超曲线空间和更普通的方块, 如恒定曲线空格和矩阵元件等产品, 有利于近似结结节双向距离。 然而, 所有这些元件的种类都是同质的, 意味着每个点的曲度分布都是一样的, 使得它们不适合于图表的本地曲线( 及相关结构属性) 。 在本文中, 我们研究图表嵌入一个更宽的宽度交错的交错调和对等数的元件。 通过在任何给定的均匀模型中添加一个单一的额外维度层面, 我们既可以计算离质曲度的曲度曲线分布方法,, 也可以算出其高比例的合成图表结构结构的重建, 。