【AAAI 2019】双曲异构信息网络嵌入，Hyperbolic Heterogeneous Information Network Embedding

题目： Hyperbolic Heterogeneous Information Network Embedding

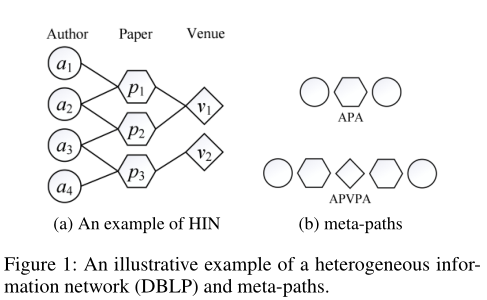
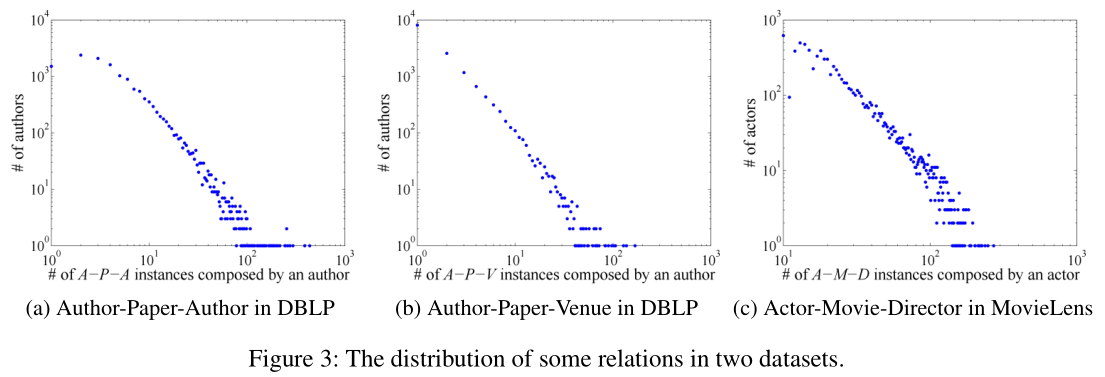
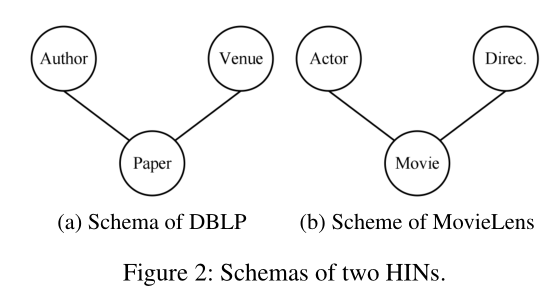
摘要： 异构信息网络嵌入(Heterogeneous information network, HIN)以将其投射到低维空间为目标，已经引起了相当多的研究关注。现有的HIN嵌入方法主要是在欧几里得空间中保留内部网络结构和语义相关性。然而，一个基本的问题是欧几里得空间是否是HIN的合适的或内在的等距空间?。近年来的研究认为，复杂网络的底层可能具有双曲几何，因为底层的双曲几何可以自然地反映复杂网络的一些特性，如层次结构和幂律结构。在本文中，我们首次尝试将HIN嵌入到双曲空间中。我们分析了两个实际HIN的结构，发现HIN中也存在幂律分布等性质。为此，我们提出了一种新的双曲异构信息网络嵌入模型。具体地说，为了捕获节点之间的结构和语义关系，我们采用元路径引导随机游走对每个节点的序列进行采样。然后利用双曲空间中的距离作为近似度量。双曲距离能满足三角不等式，并能很好地保持HIN中的传递性。我们的模型使节点及其邻域具有小的双曲线距离。进一步推导出有效的优化策略，迭代更新双曲嵌入。实验结果表明，该模型不仅在网络重构和链路预测任务上具有优越的性能，而且在HIN中通过可视化显示了捕获层次结构的能力。