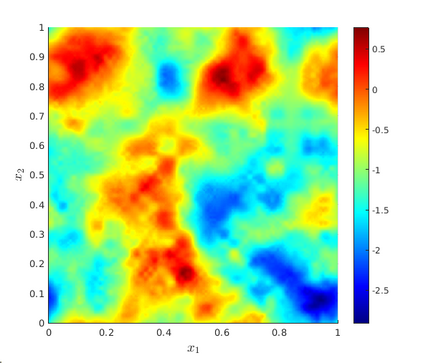
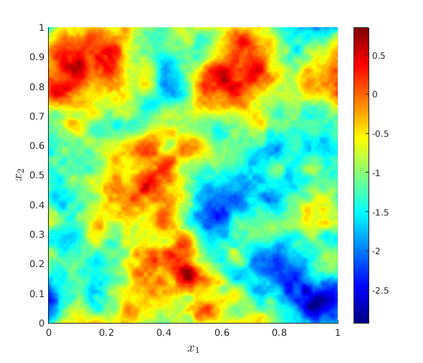
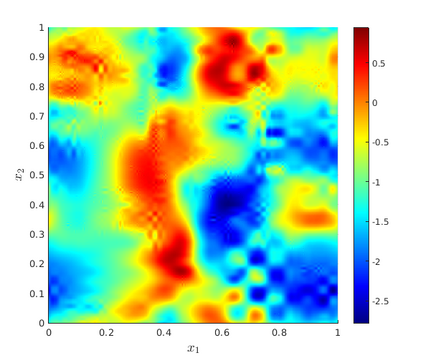
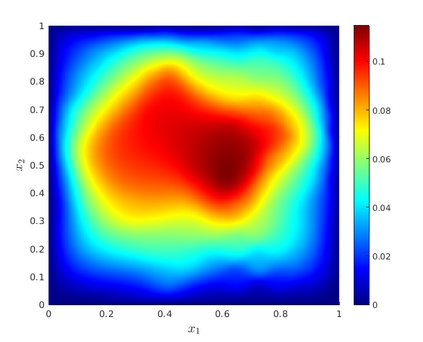
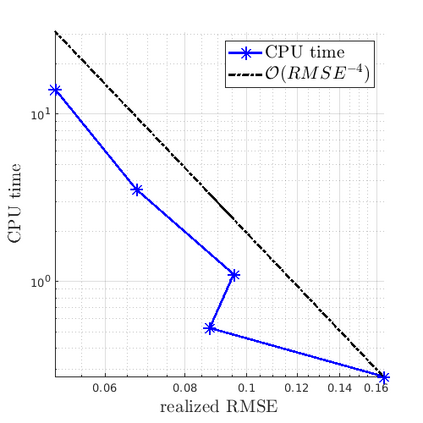
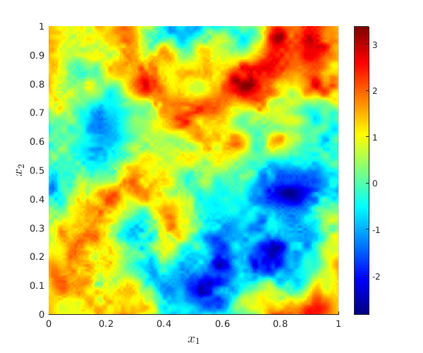
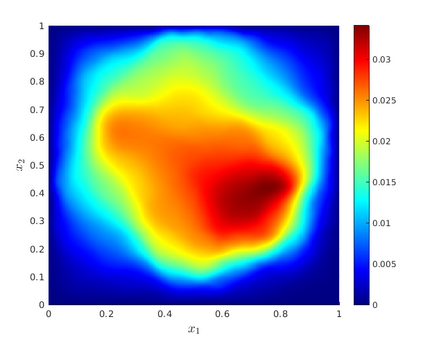
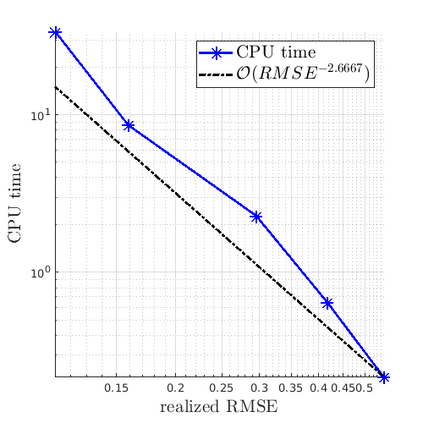
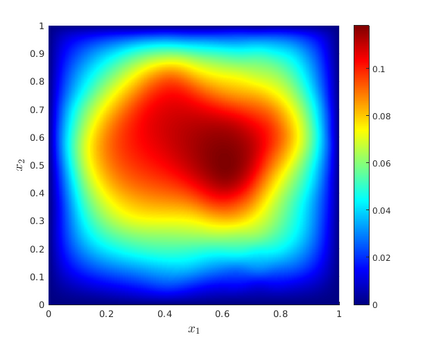
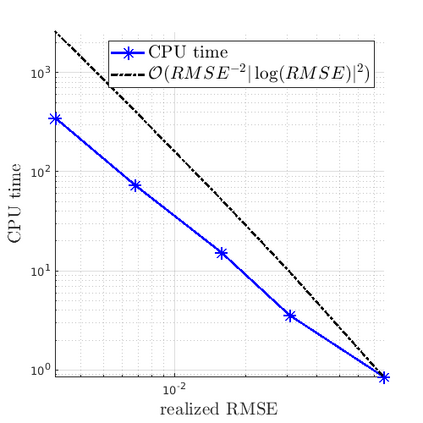
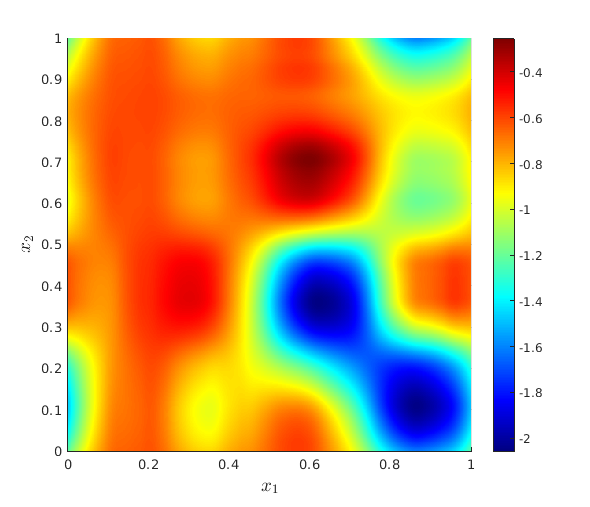
We develop a multilevel Monte Carlo (MLMC)-FEM algorithm for linear, elliptic diffusion problems in polytopal domain $\mathcal D\subset \mathbb R^d$, with Besov-tree random coefficients. This is to say that the logarithms of the diffusion coefficients are sampled from so-called Besov-tree priors, which have recently been proposed to model data for fractal phenomena in science and engineering. Numerical analysis of the fully discrete FEM for the elliptic PDE includes quadrature approximation and must account for a) nonuniform pathwise upper and lower coefficient bounds, and for b) low path-regularity of the Besov-tree coefficients. Admissible non-parametric random coefficients correspond to random functions exhibiting singularities on random fractals with tunable fractal dimension, but involve no a-priori specification of the fractal geometry of singular supports of sample paths. Optimal complexity and convergence rate estimates for quantities of interest and for their second moments are proved. A convergence analysis for MLMC-FEM is performed which yields choices of the algorithmic steering parameters for efficient implementation. A complexity (``error vs work'') analysis of the MLMC-FEM approximations is provided.
翻译:我们开发了一个多层次的蒙特卡洛(MLMC)-FEM 算法,用于多式域($\mathcal D\subset\mathb R ⁇ d$)的线性、椭圆性扩散问题,使用Besov-tree随机系数。这就是说,扩散系数的对数是从所谓的Besov-tree先前的对数中抽样的,这些对数最近被提议用来模拟科学和工程中的分形现象的数据。对椭圆形PDE的完全离散的FEM 的数值分析包括二次方位近似,并且必须考虑到(a) 非统一路径的上下系数框,以及(b) Besov-tree系数的低路径常态性。可以接受的非参数对应随机函数,显示随机的分形现象在科学和工程中的分形,但并不涉及样本路径的单形支持的微分数几何几何几何几何几何几何几何测法。MMC 最佳的复杂度和趋同比率估计利息数量及其第二个时段的精度,对Msov-L的精确度进行了EMF的精度分析。