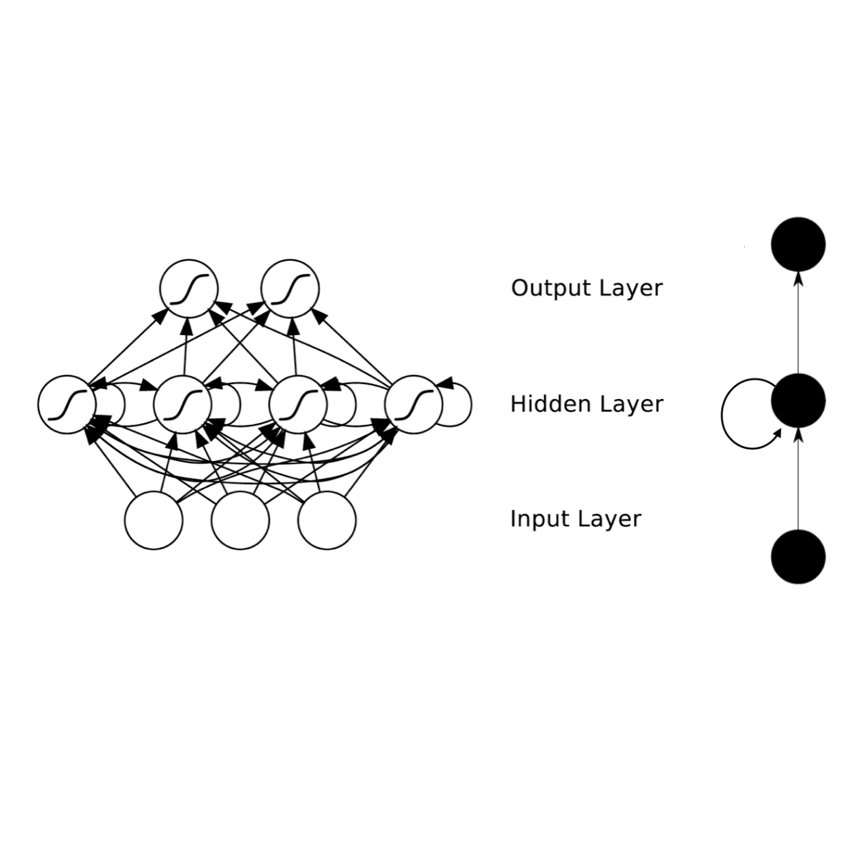
We consider the Bayesian optimal filtering problem: i.e. estimating some conditional statistics of a latent time-series signal from an observation sequence. Classical approaches often rely on the use of assumed or estimated transition and observation models. Instead, we formulate a generic recurrent neural network framework and seek to learn directly a recursive mapping from observational inputs to the desired estimator statistics. The main focus of this article is the approximation capabilities of this framework. We provide approximation error bounds for filtering in general non-compact domains. We also consider strong time-uniform approximation error bounds that guarantee good long-time performance. We discuss and illustrate a number of practical concerns and implications of these results.
翻译:我们认为贝叶斯最佳过滤问题:即从观察序列中估计潜在时间序列信号的某些有条件统计数据; 古典方法往往依赖于假设或估计过渡和观察模型的使用; 相反,我们制定通用的经常性神经网络框架,并试图直接从观测投入到理想的估测员统计数据中了解循环图解; 本条的主要重点是这一框架的近似能力; 我们为一般非契约领域的过滤提供近似误差界限; 我们还考虑强有力的时间统一近似误差界限,以保证良好的长期性能; 我们讨论并举例说明这些结果的一些实际关切和影响。