Retrospective Approximation for Smooth Stochastic Optimization

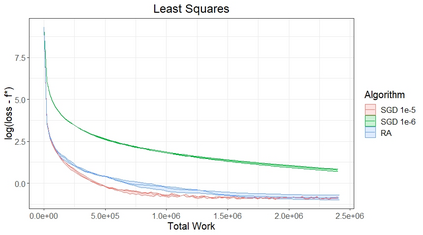
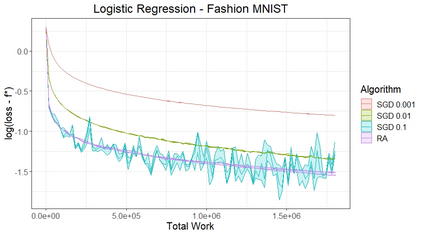
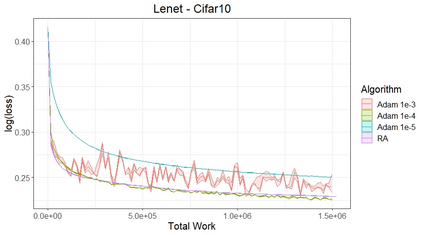
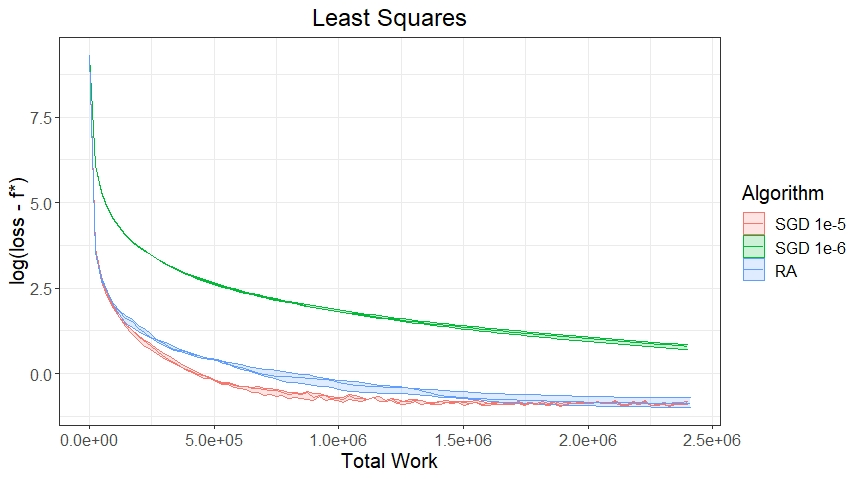
Stochastic Gradient (SG) is the defacto iterative technique to solve stochastic optimization (SO) problems with a smooth (non-convex) objective $f$ and a stochastic first-order oracle. SG's attractiveness is due in part to its simplicity of executing a single step along the negative subsampled gradient direction to update the incumbent iterate. In this paper, we question SG's choice of executing a single step as opposed to multiple steps between subsample updates. Our investigation leads naturally to generalizing SG into Retrospective Approximation (RA) where, during each iteration, a "deterministic solver" executes possibly multiple steps on a subsampled deterministic problem and stops when further solving is deemed unnecessary from the standpoint of statistical efficiency. RA thus rigorizes what is appealing for implementation -- during each iteration, "plug in" a solver, e.g., L-BFGS line search or Newton-CG, as is, and solve only to the extent necessary. We develop a complete theory using relative error of the observed gradients as the principal object, demonstrating that almost sure and $L_1$ consistency of RA are preserved under especially weak conditions when sample sizes are increased at appropriate rates. We also characterize the iteration and oracle complexity (for linear and sub-linear solvers) of RA, and identify a practical termination criterion leading to optimal complexity rates. To subsume non-convex $f$, we present a certain "random central limit theorem" that incorporates the effect of curvature across all first-order critical points, demonstrating that the asymptotic behavior is described by a certain mixture of normals. The message from our numerical experiments is that the ability of RA to incorporate existing second-order deterministic solvers in a strategic manner might be important from the standpoint of dispensing with hyper-parameter tuning.