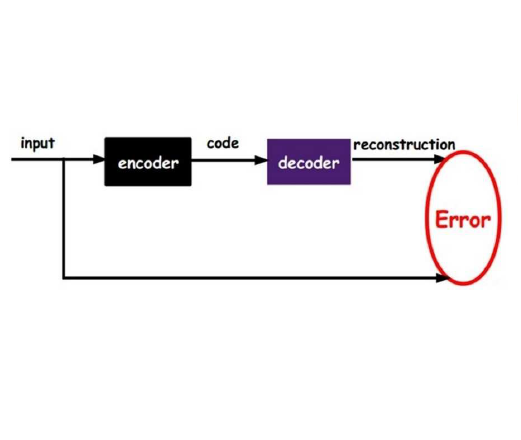
Shape encoding and shape analysis are valuable tools for comparing shapes and for dimensionality reduction. A specific framework for shape analysis is the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework, which is capable of shape matching and dimensionality reduction. Researchers have recently introduced neural networks into this framework. However, these works can not match more than two objects simultaneously or have suboptimal performance in shape variability modeling. The latter limitation occurs as the works do not use state-of-the-art shape encoding methods. Moreover, the literature does not discuss the connection between the LDDMM Riemannian distance and the Riemannian geometry for deep learning literature. Our work aims to bridge this gap by demonstrating how LDDMM can integrate Riemannian geometry into deep learning. Furthermore, we discuss how deep learning solves and generalizes shape matching and dimensionality reduction formulations of LDDMM. We achieve both goals by designing a novel implicit encoder for shapes. This model extends a neural network-based algorithm for LDDMM-based pairwise registration, results in a nonlinear manifold PCA, and adds a Riemannian geometry aspect to deep learning models for shape variability modeling. Additionally, we demonstrate that the Riemannian geometry component improves the reconstruction procedure of the implicit encoder in terms of reconstruction quality and stability to noise. We hope our discussion paves the way to more research into how Riemannian geometry, shape/image analysis, and deep learning can be combined.
翻译:暂无翻译