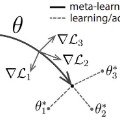
In few-shot learning scenarios, the challenge is to generalize and perform well on new unseen examples when only very few labeled examples are available for each task. Model-agnostic meta-learning (MAML) has gained the popularity as one of the representative few-shot learning methods for its flexibility and applicability to diverse problems. However, MAML and its variants often resort to a simple loss function without any auxiliary loss function or regularization terms that can help achieve better generalization. The problem lies in that each application and task may require different auxiliary loss function, especially when tasks are diverse and distinct. Instead of attempting to hand-design an auxiliary loss function for each application and task, we introduce a new meta-learning framework with a loss function that adapts to each task. Our proposed framework, named Meta-Learning with Task-Adaptive Loss Function (MeTAL), demonstrates the effectiveness and the flexibility across various domains, such as few-shot classification and few-shot regression.
翻译:在几近的学习情景中,挑战在于如何概括和很好地运用新的无形实例,因为每项任务只有很少的贴标签例子。模型-不可知元学习(MAML)作为具有代表性的微小学习方法之一,因其灵活性和对各种问题的适用性而赢得了欢迎。然而,MAML及其变体往往采用简单的损失功能,而没有任何附带损失功能或正规化条件,可以帮助实现更好的概括化。问题在于每个应用程序和任务可能需要不同的辅助损失功能,特别是在任务多种多样和不同的情况下。我们不试图为每项应用程序和任务手工设计辅助损失功能,而是采用新的、适合每项任务的损失功能的元学习框架。我们拟议的框架名为“Meta-Learning with TAT-Apative损失函数”(METAL),显示了不同领域的效力和灵活性,例如:微小的分类和微小的回归。