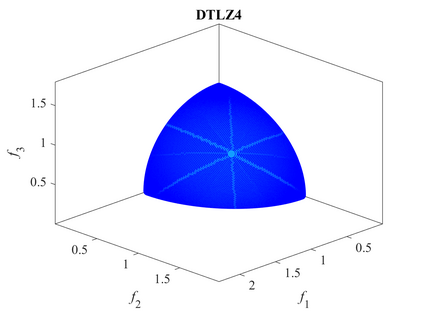
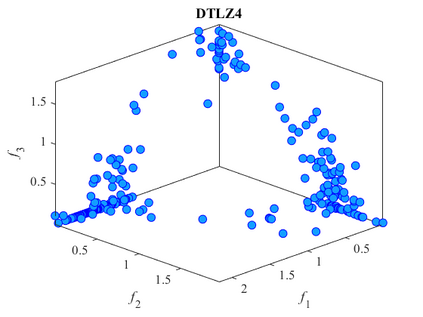
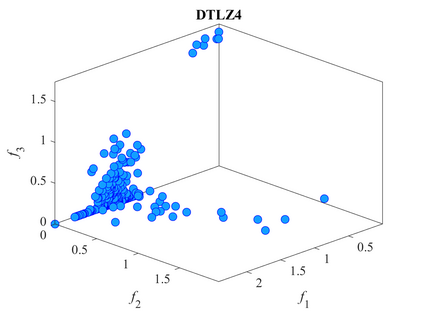
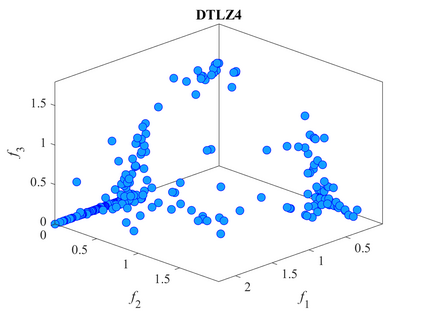
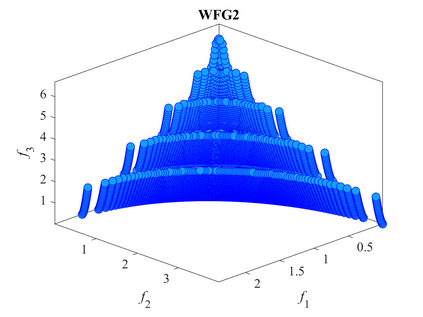
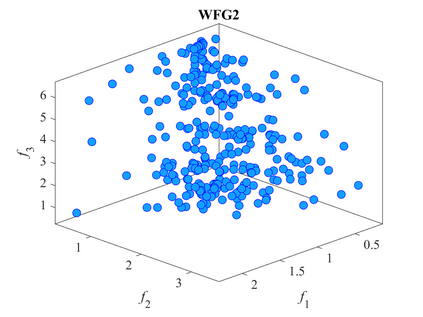
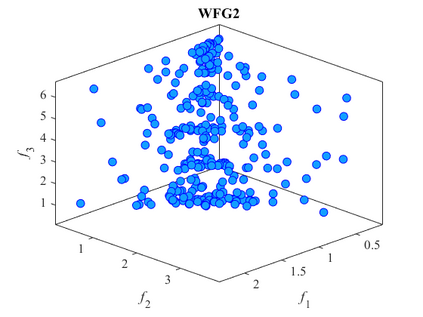
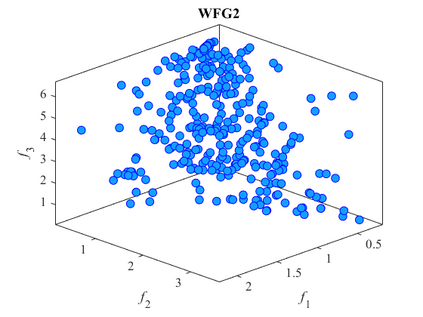
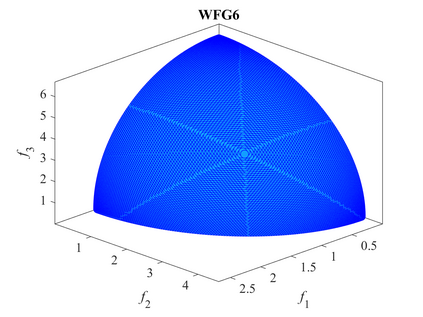
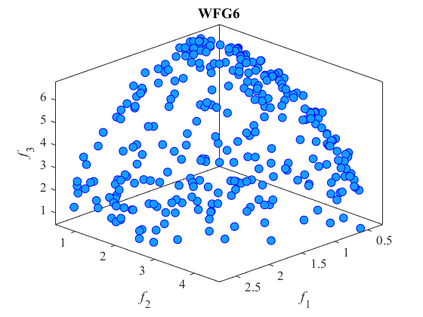
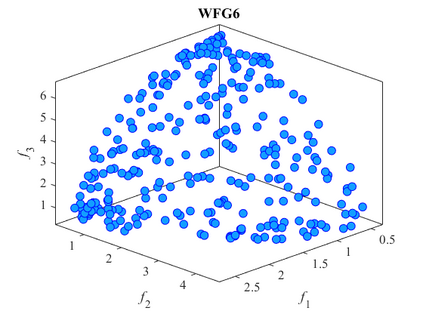
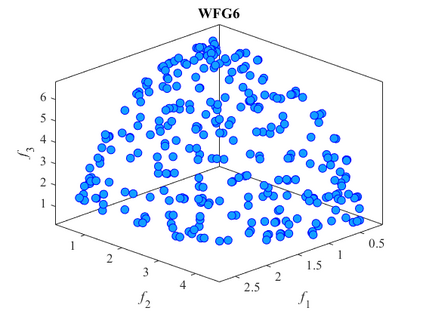
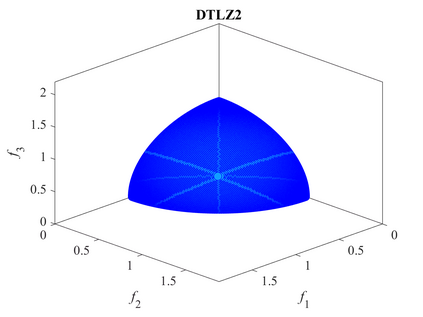
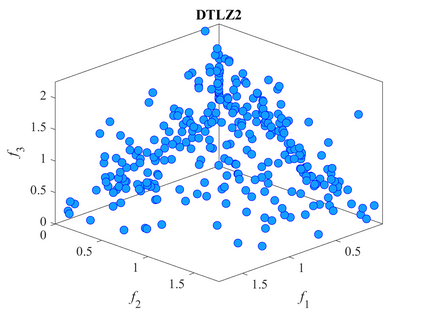
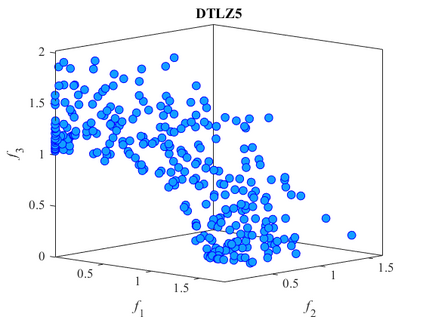
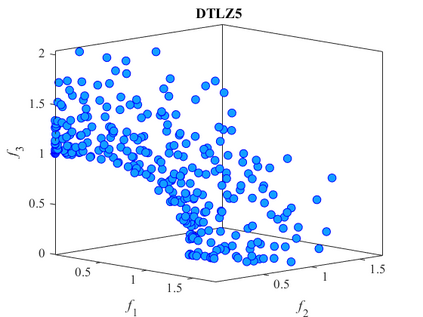
Multi-objective optimization problems whose objectives have different evaluation costs are commonly seen in the real world. Such problems are now known as multi-objective optimization problems with heterogeneous objectives (HE-MOPs). So far, however, only a few studies have been reported to address HE-MOPs, and most of them focus on bi-objective problems with one fast objective and one slow objective. In this work, we aim to deal with HE-MOPs having more than two black-box and heterogeneous objectives. To this end, we develop a multi-objective Bayesian evolutionary optimization approach to HE-MOPs by exploiting the different data sets on the cheap and expensive objectives in HE-MOPs to alleviate the search bias caused by the heterogeneous evaluation costs for evaluating different objectives. To make the best use of two different training data sets, one with solutions evaluated on all objectives and the other with those only evaluated on the fast objectives, two separate Gaussian process models are constructed. In addition, a new acquisition function that mitigates search bias towards the fast objectives is suggested, thereby achieving a balance between convergence and diversity. We demonstrate the effectiveness of the proposed algorithm by testing it on widely used multi-/many-objective benchmark problems whose objectives are assumed to be heterogeneously expensive.
翻译:目标具有不同评价成本的多目标优化问题在现实世界中是常见的。这些问题现在被称为具有不同目标的多目标优化问题(HE-MOPs ) 。然而,到目前为止,只报告了若干项研究来针对HE-MOPs,其中多数侧重于一个快速目标和一个缓慢目标的双目标问题。在这项工作中,我们的目标是与两个以上黑箱和不同目标的HE-MOs打交道。为此,我们为HE-MOs制定了一种多目标的贝叶西亚进化优化方法,利用HE-MOs中廉价和昂贵目标的不同数据集来缓解不同目标评估成本造成的搜索偏差。为了最佳利用两种不同的培训数据集,一种是对所有目标都进行评价的解决方案,另一种是只对快目标进行评价的解决方案。此外,我们提出了两个单独的高叶进程模型。此外,我们提出了一个新的购置功能,可以减少搜索对快目标的偏差,从而实现趋同和多样性之间的平衡。我们通过测试广泛使用的多/曼基目标,我们用其假设为具有成本效益。