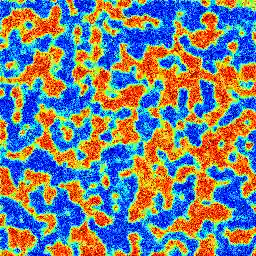
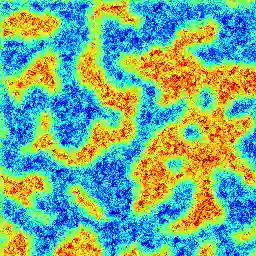
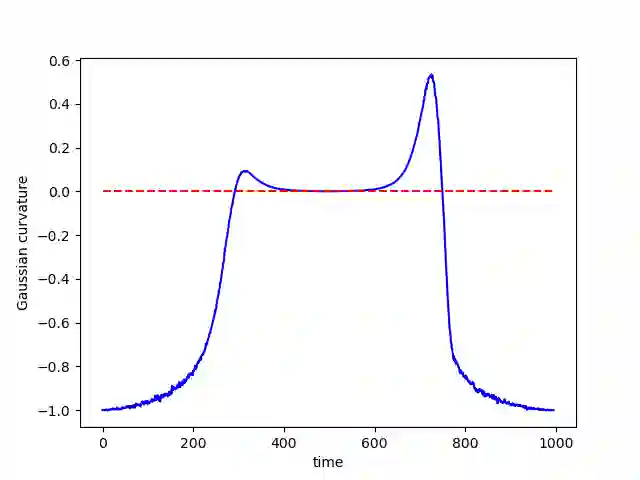
Random field models are mathematical structures used in the study of stochastic complex systems. In this paper, we compute the shape operator of Gaussian random field manifolds using the first and second fundamental forms (Fisher information matrices). Using Markov Chain Monte Carlo techniques, we simulate the dynamics of these random fields and compute the Gaussian curvature of the parametric space, analyzing how this quantity changes along phase transitions. During the simulation, we have observed an unexpected phenomenon that we called the \emph{curvature effect}, which indicates that a highly asymmetric geometric deformation happens in the underlying parametric space when there are significant increase/decrease in the system's entropy. This asymmetric pattern relates to the emergence of hysteresis, leading to an intrinsic arrow of time along the dynamics.
翻译:随机字段模型是用于研究随机复杂系统的数学结构。 在本文中, 我们使用第一和第二种基本形式( Fisher 信息矩阵) 计算高森随机字段元件的形状操作器。 我们使用 Markov 链子 Monte Carlo 技术, 模拟这些随机字段的动态, 并计算高萨参数空间的曲线, 分析此数量在阶段转换过程中的变化 。 在模拟中, 我们观察到一个我们称之为 emph{ curvure effect} 的意外现象, 这表明当系统昆虫出现大幅增长/ 下降时, 基础参数空间发生了高度不对称的几何形变形。 这种不对称模式与歇斯氏体的出现有关, 导致动态中的时间的内在箭头。