图神经网络的困境，用微分几何和代数拓扑解决

会员服务 ·

图神经网络的困境，用微分几何和代数拓扑解决

2022 年 3 月 27 日 机器之心

选自towardsdatascience

作者：Michael Bronstein

机器之心编译

编辑：Juniper

微分几何和代数拓扑在主流机器学习中并不常见。在本系列文章中，作者展示了如何使用这些领域的工具重新解释图神经网络并解决一些常见困境。

本文的作者是 Twitter 首席科学家、DeepMind 人工智能教授 Michael Bronstein。以下是博客原文。

对称，无论从广义还是狭义的角度讲，都是人类一直以来试图理解和创造秩序与美的一种观念。

——Hermann Weyl

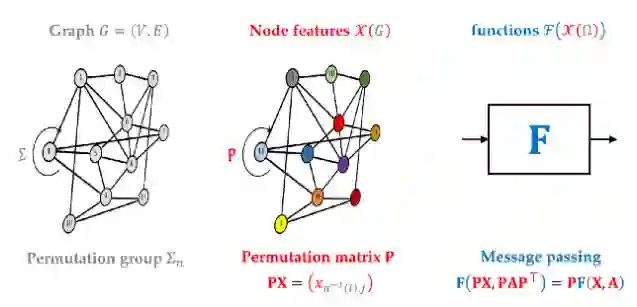
Hermann Weyl 这种诗意的描述强调了对称性在科学中的基石作用。Felix Klein 在 1872 年的「Erlangen Programme」中用对称群表征几何。这不仅是数学上的一个突破，即统一了「几何大家庭」，还推进了现代物理理论的发展，这些理论可以完全从对称性的第一原理推导出来。几何深度学习领域也出现了类似的原则，通过群不变性和等变性能够推导出大多数流行神经网络架构的通用蓝图。

图神经网络可以被认为是几何深度学习蓝图的一个特例，其构建模块是具有对称群的域（在这种情况下是具有置换群的图）、域上的信号（节点特征）和此类信号的群等变函数（消息传递）。

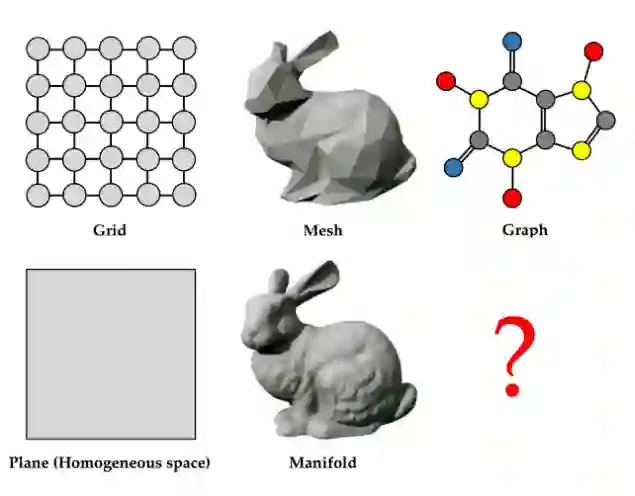
几何深度学习蓝图可以应用于不同的领域，例如 grid、mesh 或图 (graph)。然而，前两者具有明确的连续形式的类比对象，grid 可以被认为是欧几里得空间或更一般的均匀空间（如球体）的离散化，mesh 则是二维流形的常见离散化），图却没有直接的连续形式的类比。这种不可类比有点令人不安，因此我们决定仔细研究用于图学习的连续模型。

图神经网络扩散。图神经网络 (GNN) 通过在图上执行某种形式的消息传递来学习。其中，特征通过边从一个节点传递到另一个节点。这种机制与图上的扩散过程有关，可以用称为「扩散方程」的偏微分方程 (PDE) 形式表示。我们最近在一篇论文中展示了这种具有非线性可学习扩散函数的 PDE 的离散化（称为 GRAND），泛化了一大类 GNN 架构，例如图注意力网络（GAT。

PDE 的思维方式提供了多种优势，例如可以利用兼具稳定性和收敛性的高效数值求解器（例如隐式、多步、自适应和 multigrid 方案）。其中一些求解器在流行的 GNN 架构中没有直接的类比，可能会促成一些新型图神经网络设计。由于我们考虑的扩散 PDE 可以看作是一些相关能量的梯度流，因此这种架构可能比典型架构更易于解释。

同时，虽然 GRAND 模型提供连续时间来代替传统 GNN 中的层，但方程的空间部分仍然是离散的，并且依赖于输入图。重要的是，在这个扩散模型中，域（图）是固定的，其上定义的某些属性会演化。

微分几何中常用的一个不同概念是几何流（geometric flow），域本身的属性不断演化。我的博士生导师 Ron Kimmel 等研究者 20 世纪 90 年代在图像处理领域就采用了这个想法。他们将图像建模为嵌入在联合位置和颜色空间中的流形，并通过 PDE 对它们进行推导演化，以最小化嵌入的谐波能量。这样的偏微分方程称为贝尔特拉米流（Beltrami flow），具有各向同性非欧几里得扩散的形式，并产生保边图像去噪。

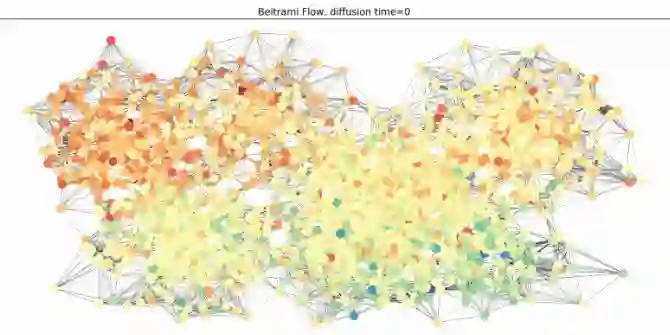
我们将这种范式应用于「Beltrami 神经扩散（BLEND）」框架中的图。图的节点现在由位置坐标和特征坐标来表征，这两个坐标都是经过演化的，并且都决定了扩散性。在这种思维模式下，图本身就变成了一个辅助角色：它可以从位置坐标生成（例如作为 k - 最近邻图）并在整个演化过程中重新连接。下图说明了这种同时演化的过程。

图的表达能力

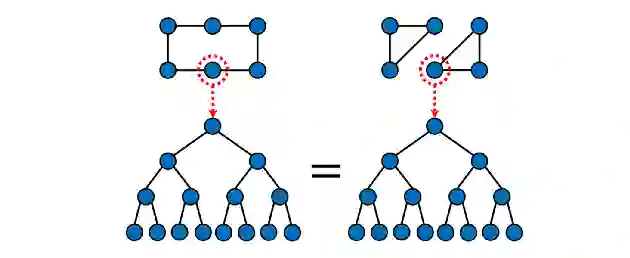
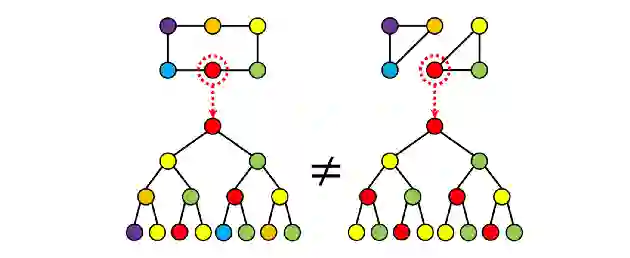
在最近的工作中，人们对图神经网络（GNN）的表达能力给予了极大的关注。消息传递的 GNN 等价于 Weisfeiler-Lehman 图同构测试（一种通过迭代颜色细化来确定两个图是否在结构上等价 (同构) 的经典方法）。这个检验是一个必要但不充分条件：事实上，一些非同构图可能会通过 Weisfeler-Lehman 测试。下图说明了 GNN 传递消息过程中该测试「看到」了什么：两个高亮显示的节点看起来没有什么区别，然而这两个图显然具有不同的结构：

位置编码 。解决这个问题的一个常见方法是通过为节点分配一些额外的特征来给节点「着色」，这些特征保证了图中节点的角色或「位置」。由于位置编码在 Transformer 中已得到普及，因此位置编码成为增加图神经网络表达能力的常用方法。

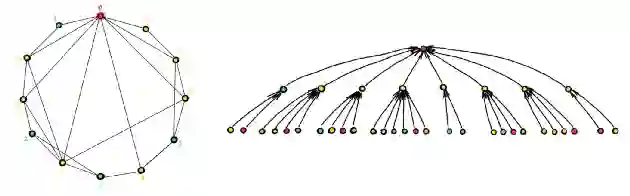
位置编码为图的节点分配了额外的特征，允许消息传递获得比 Weisfeiler-Lehman 测试更高的表达能力。然而，对于位置编码，并没有一个「规范」的选择。

也许最直接的方法是赋予每个节点一个随机特征；然而，这种方法虽然可以更具表达性，但泛化能力较差（因为不可能在两个图中重现随机特征）。图拉普拉斯算子的特征向量提供了图的领域保持嵌入，并已成功用作位置编码。最后，我们（与 Giorgos Bouritsas 和 Fabrizio Frasca 合著）在一篇论文中表明，图的子结构计数可以用作位置或「结构」编码的一种形式，这说明它比基本的 Weisfeiler-Lehman 测试更强大。

然而，位置编码有多种选择，如何选择以及哪种方法在哪种情况下效果更好，都没有明确的答案。我相信像 BLEND 这样的几何流可以根据这个问题来解释：通过非欧几里得扩散来演化图的位置坐标，位置编码可以适用于下游任务。因此，答案是「视情况而定」：最佳位置编码是手头数据和任务的函数。

高阶消息传递 。表达性的另一种选择是放弃根据节点和边来考虑图，而是把图看作单元复合体（cell complex）对象的示例，单元复合体是代数拓扑领域的主要研究对象之一。在这种方法中，节点是 0-cell，边是 1-cell。不必止步于此：我们可以构造如下图所示的 2-cells（面），这使得上述示例中的两个图可以完美区分：

在我最近与 Cristian Bodnar 和 Fabrizio Frasca 合作的两篇论文中，我们表明可以构建一个「提升变换」，用高阶单元来增强图，从而在这些单元上可以执行更复杂的分层消息传递形式。该方案可被证明比 Weisfeiler-Lehman 测试的表达能力更强，并且在计算化学领域给出了有望的结果：比建模为图，建模为单元复合体表现更好。

「over-squashing」现象

GNN 的另一个常见问题是「over-squashing」现象，或者由于输入图的某些结构特征，消息传递无法有效地传播信息。oversquashing 通常发生在体积呈指数增长的图中，例如小世界网络以及依赖于远程信息的问题。换句话说，GNN 作用的输入图并不总是对消息传递友好。

「小世界」图中快速增长的邻居数量通常是 GNN 中观察到的过度挤压现象的根源。

从实验可以观察到，将输入图与计算图解耦并允许在不同的图上传递消息有助于缓解这一问题。这种技术通常被称为「图重新布线（graph rewiring）」。

事实上，许多流行的 GNN 架构都实现了某种形式的图重构，可以采用邻域采样（最初在 GraphSAGE 中提出以应对可扩展性）或多跳滤波器的形式。上面讨论的拓扑消息传递也可以看作是重新布线的一种形式，远距离节点之间的信息流可以认为是通过高阶单元的「捷径」。Alon 和 Yahav [23] 表明，即使像使用全连接图这样简单的方法也可能有助于改善图 ML 问题中的 over-squashing。

Klicpera 等研究者宣称「扩散改进了图学习」，提出了一个通用的 GNN 预处理步骤（DIGL），包括通过扩散过程来去噪图的连通性。总体而言，尽管进行了重要的实验研究，但 over-squashing 现象一直令人难以捉摸。我们最近在一篇论文中表明：导致 over-squashing 的瓶颈可归因于图的局部几何特性。具体来说，通过定义 Ricci 曲率的图类比，我们可以证明罪魁祸首是 negatively-curved 边。因此出现了一种类似于「反向 Ricci 流」的图重新布线过程，该过程去除有问题的边并生成一个更易于消息传递的图，同时在结构上与输入图相似。

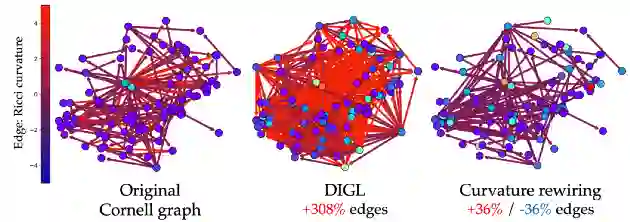
使用基于扩散的方法（DIGL，中）和基于曲率的方法（Ricci，右）重新连接康奈尔图（左）的示例。基于曲率的方法显著减少了瓶颈，同时更接近于原始图结构。

总结

这些例子表明，微分几何和代数拓扑为图机器学习中重要且具有挑战性的问题带来了新的视角。在本系列的后续文章中，我将更详细地展示如何使用这些领域的工具来解决上述图神经网络问题。第二部分将讨论代数拓扑如何提高 GNN 的表达能力。第三部分将讲解几何扩散偏微分方程。第四部分将展示 over-squashing 现象与图曲率有何相关，并提供一种受 Ricci 流启发的图重新布线的新型几何方法。