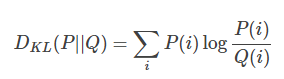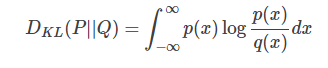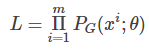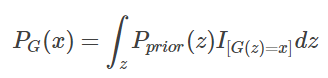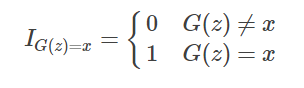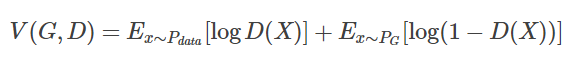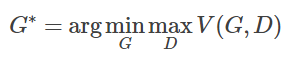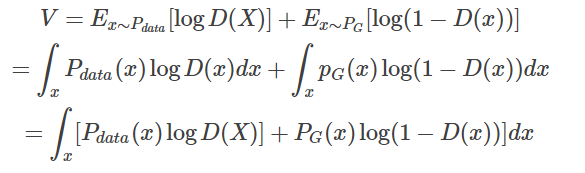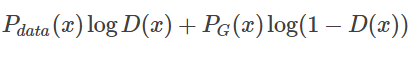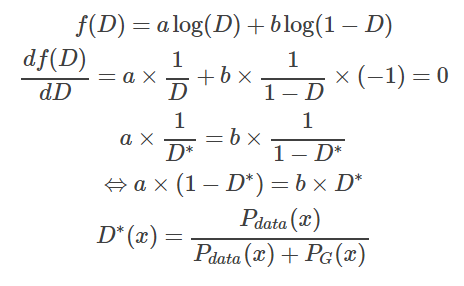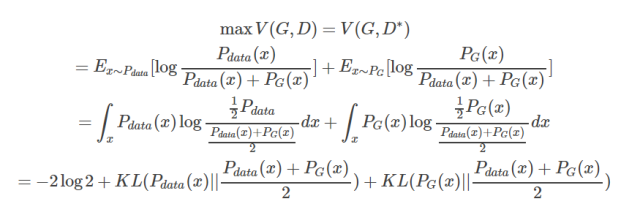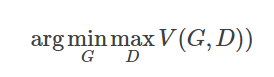GAN的数学原理

  GAN的数学推导  

作者：Sherlock

来源：机器学习算法与自然语言处理

前面我们讲了一下GAN的基本思想，最近看了一下GAN的论文，又恰好看到了李宏毅老师的课程，感觉里面的数学推导很有意思，所以准备写下来以备之后查阅。

首先需要一点预备知识，KL divergence，这是统计中的一个概念，是衡量两种概率分布的相似程度，其越小，表示两种概率分布越接近。 对于离散的概率分布，定义如下

对于连续的概率分布，定义如下

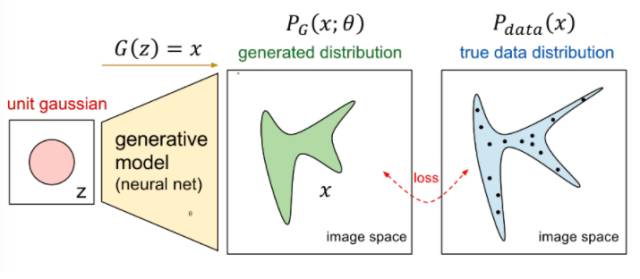
根据我们之前讲的内容，我们要做的事情就如下图所示

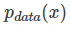
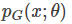
我们想要将一个随机高斯噪声z通过一个生成网络G得到一个和真的数据分布差不多的生成分布。

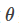
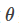
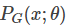
其中的参数是网络的参数决定的，我们希望找到 使得和尽可能接近。

Maximun Likelihood Estimation

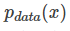
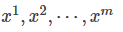
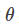
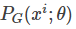
我们从真实数据分布 里面取样m个点，，根据给定的参数我们可以计算如下的概率 ，那么生成这m个样本数据的似然(likelihood)就是

我们想要做的事情就是找到  θ∗来最大化这个似然估计

而  PG(x;θ)如何算出来呢？

里面的I表示示性函数，也就是

这样我们其实根本没办法求出这个  PG(x) 出来，这就是生成模型的基本想法。

Basic Idea of GAN

• Generator G

• G是一个生成器，给定先验分布  Pprior(z)我们希望得到生成分布  PG(x)，这里很难通过极大似然估计得到结果

• Discriminator D

• D是一个函数，来衡量  PG(x) 与  Pdata(x)之间的差距，这是用来取代极大似然估计

首先定义函数V(G, D)如下




我们可以通过下面的式子求得最优的生成模型


是不是感觉很晕，为什么定义了一个V(G, D)然后通过求max和min就能够取得最优的生成模型呢？




首先我们只考虑 maxDV(G,D)，看其表示什么含义。




在给定G的前提下，我们要取一个合适的D使得V(G, D)能够取得最大值，这就是简单的微积分。




对于这个积分，要取其最大值，我们希望对于给定的x，积分里面的项是最大的，也就是我们希望取到一个最优的  D∗最大化下面这个式子




在数据给定，G给定的前提下， Pdata(x)与PG(x) 都可以看作是常数，我们可以分别用a,b来表示他们，这样我们就可以得到如下的式子




这样我们就求得了在给定G的前提下，能够使得V(D)取得最大值的D，我们将D代回原来的V(G, D)，得到如下的结果

看到这里我们其实就已经推导出了为什么这么衡量是有意义的，因为我们取D使得V(G,D)取得max值。




这个时候这个max值是由两个KL divergence构成的，相当于这个max的值就是衡量  PG(x)与Pdata(x)的差异程度，所以这个时候，我们取

就能够取到G使得这两种分布的差异性最小，这样自然就能够生成一个和原分布尽可能接近的分布。




同时这样也摆脱了计算极大似然估计，所以GAN本质是改变了训练的过程。




博客地址：https://sherlockliao.github.io/2017/06/20/gan_math/

---

☞  哈尔莫斯：怎样做数学研究

☞  扎克伯格2017年哈佛大学毕业演讲

☞  线性代数在组合数学中的应用

☞  你见过真的菲利普曲线吗？

☞  支持向量机(SVM)的故事是这样子的

☞  深度神经网络中的数学，对你来说会不会太难？

☞  编程需要知道多少数学知识？

☞  陈省身——什么是几何学

☞  模式识别研究的回顾与展望

☞  曲面论

☞  自然底数e的意义是什么？

☞  如何向5岁小孩解释什么是支持向量机（SVM）？

☞  华裔天才数学家陶哲轩自述

☞  代数，分析，几何与拓扑，现代数学的三大方法论

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域。

稿件一经采用，我们将奉上稿酬。

投稿邮箱：math_alg@163.com