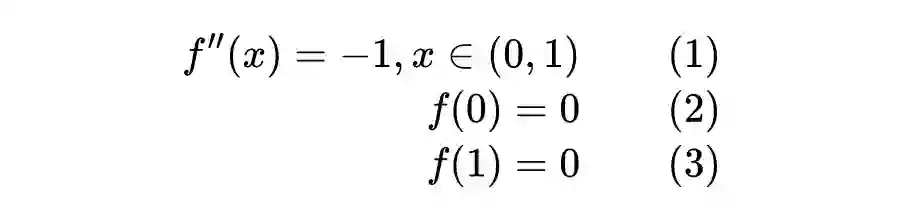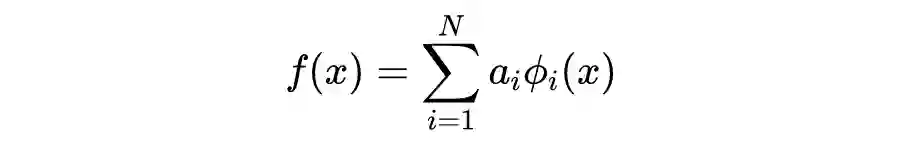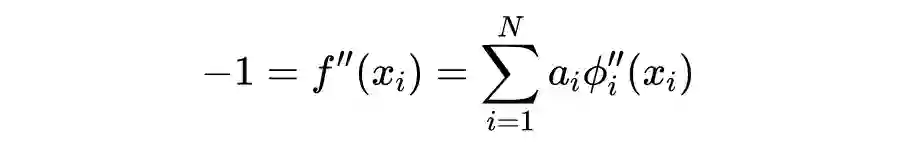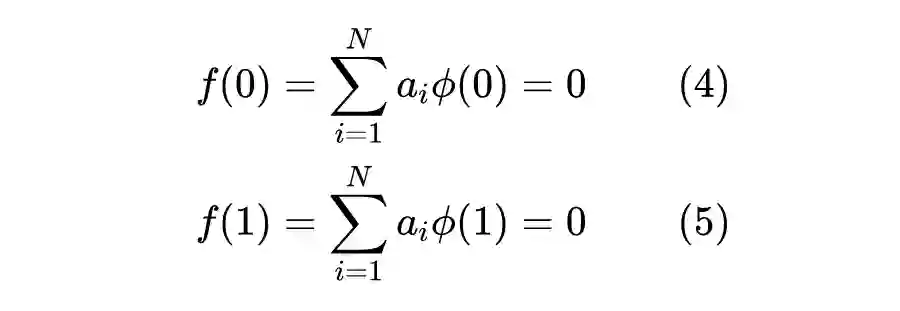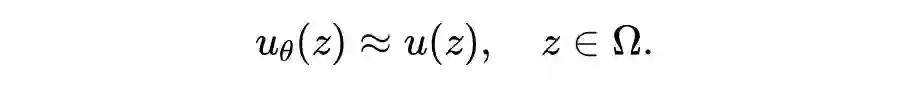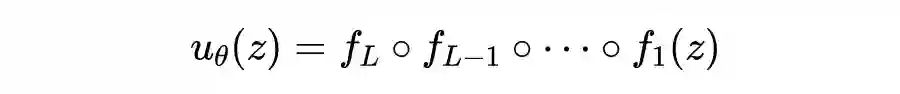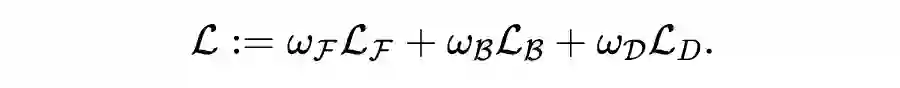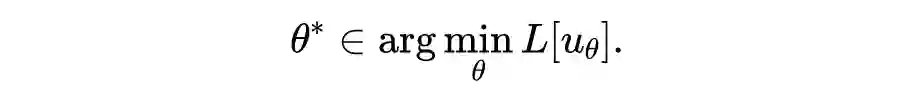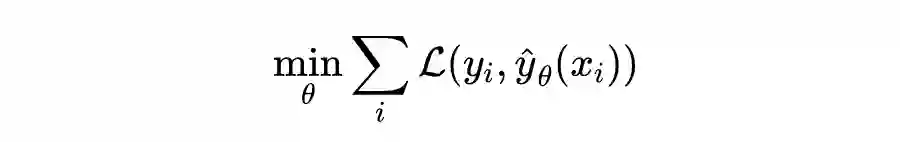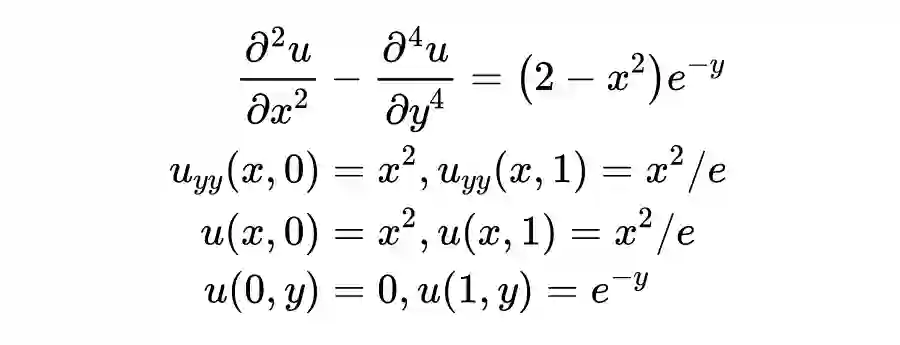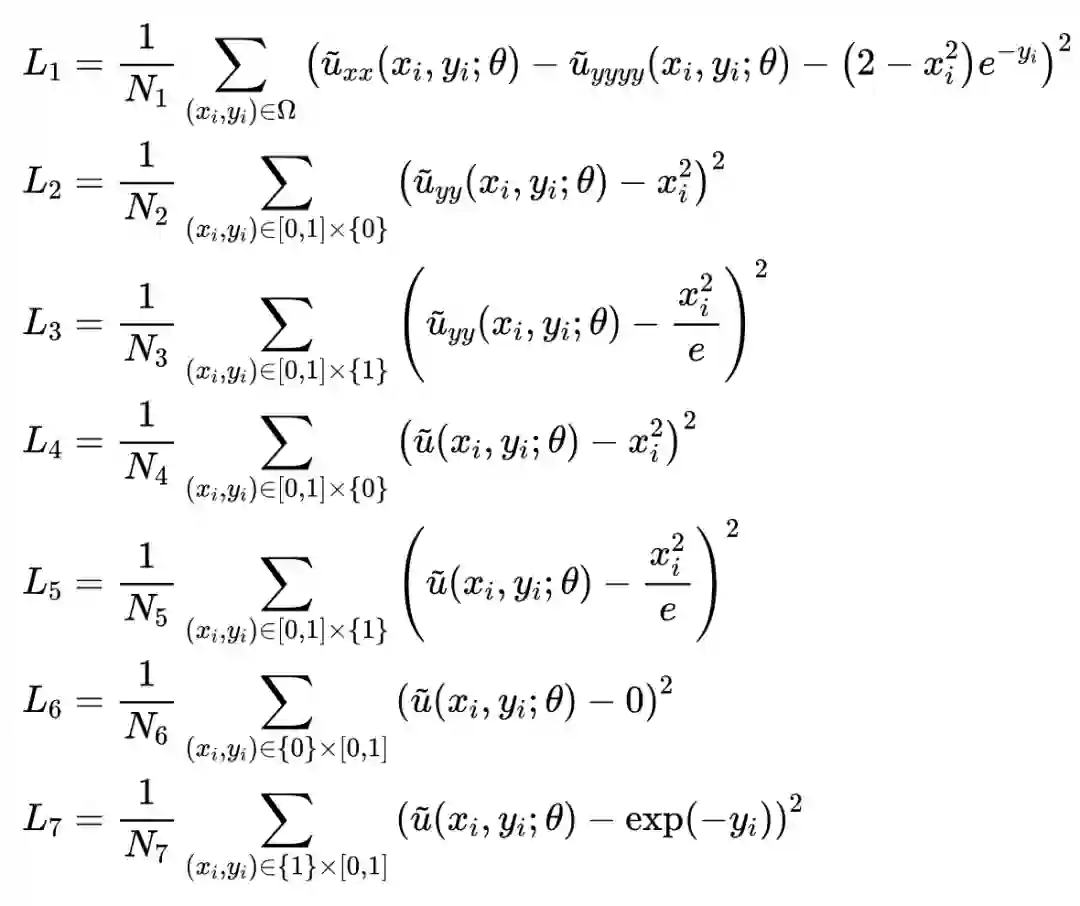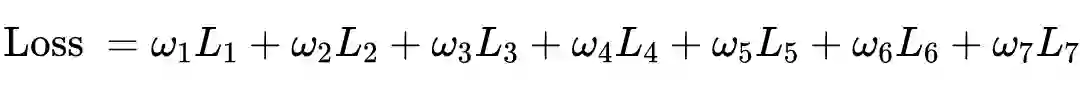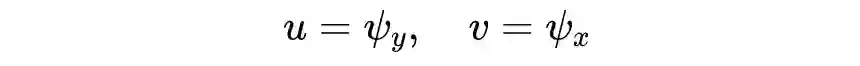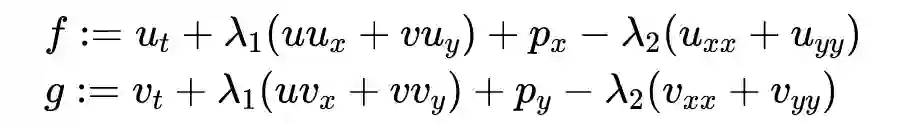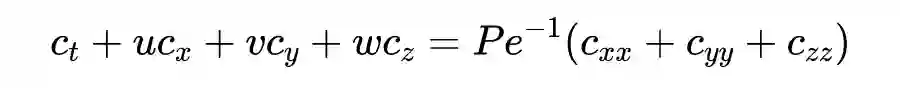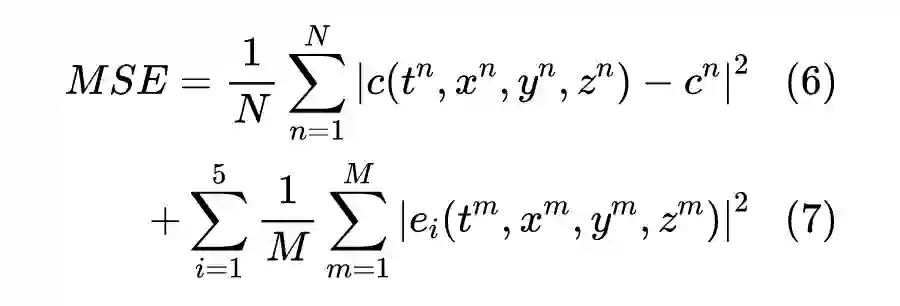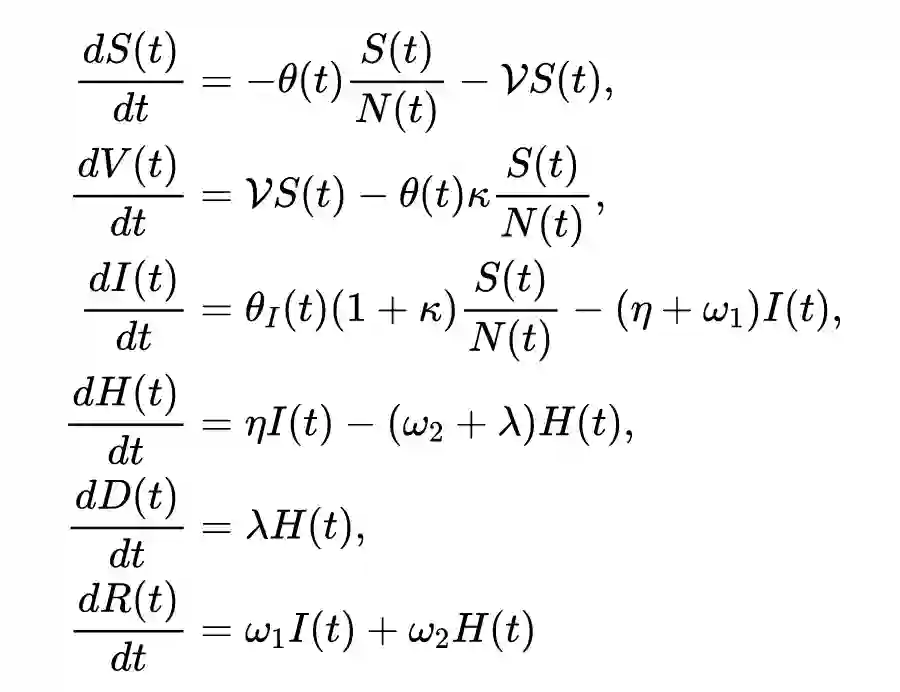内嵌物理知识神经网络(PINN)是个坑吗?

从无网格方法到内嵌物理知识的神经网络
内嵌物理知识神经网络 (Physics Informed Neural Network,简称 PINN) 是一种科学机器在传统数值领域的应用方法,特别是用于解决与偏微分方程 (PDE) 相关的各种问题,包括方程求解、参数反演、模型发现、控制与优化等。
先简单概括,PINN 的原理就是通过训练神经网络来最小化损失函数来近似 PDE 的求解,所谓的损失函数项包括初始和边界条件的残差项,以及区域中选定点(按传统应该称为“配点”)处的偏微分方程残差。训练完成后进行推断(Inference)就可以得到时空点上的值了。
当然了,结果大家都知道,浅层神经网络在学习复杂的特征时可能会力不从心,网络宽度的增加也可能会使线性系统变得非常病态,基函数的超参选取是个问题,配点的选择当然也有讲究,无网格法有无网格法的解决方式。但如果要从神经网络,也就是 PINN 这条路子上走的话,将单层的 RBF-net 增加为多层感知机(MLP)就是件非常自然的事情了。
上面的基展开方法也可以延伸至一般伪谱方法。从数据的角度看,所谓的基就是特征,既然这种线性表征是可行的,那么利用神经网络来进行非线性表征也挺合理。
其中:
-
是包含了空间和时间的坐标; -
表示方程的解; -
是方程所在的区域; -
算子描述了控制方程; -
是控制方程的参数; -
算子描述了初值或者边界条件; -
算子描述了观测数据的方式; -
是观测数据指标集。
相比传统微分方程数值求解的描述,这里多出了第三行式子,也就是对于数据的使用,这也是 PINN 的特点之一。当然,这三个条件也不一定全都出现,比如边界条件消失,从传统数值方法的角度来看甚至不能满足定解条件。
Wang, Nanzhe, Haibin Chang, and Dongxiao Zhang. "Theory-guided auto-encoder for surrogate construction and inverse modeling." Computer Methods in Applied Mechanics and Engineering 385 (2021): 114037.
注意这跟之前提到的 Kansa 方法在计算上有了重大区别,对于线性微分方程,Kansa 方法通常也会导出线性方程组(矩阵),从而可以使用线性方程求解器对方程进行求解。但 PINN 这种神经网络不行,即使对于线性方程,也不得不使用非线性求解器(迭代优化器),比如 L-BFGS,或者神经网络训练中用得更多的 SGD、Adam 等。非线性问题的求解通常比线性问题难,这是 PINN 计算效率上一个避不开的障碍。
从这么看来,PINN 确实不是太过于新奇的东西,前人肯定想到过,这也确实如此。至少在 1994 年的文献中已经有使用 MLP 求解二维 Poisson 方程的例子:
Dissanayake, M. W. M. G., and Nhan Phan‐Thien. "Neural‐network‐based approximations for solving partial differential equations." communications in Numerical Methods in Engineering 10.3 (1994): 195-201.
当年或许还没有诸如 Pytorch、Tensorflow 或者 RTX 3090 之类的软硬工具,数值计算科学家们大概还沉迷于 Fortran 艺术中,“思维没有现在这么活络”,加上大数据的时代并没有到来,因此对这个方法并没有太大需求,导致了在后续一段时间内也一直没有太大发展。直到 2018 年开始,也就是 Raissi 他们在 Arxiv 挂出 PINN 不久,这篇文章开始迎接远超二十多年来积累到的引用量。
Raissi, Maziar, Paris Perdikaris, and George Em Karniadakis. "Physics informed deep learning (part i): Data-driven solutions of nonlinear partial differential equations." arXiv preprint arXiv:1711.10561 (2017).
上面这篇文章并没有总结早期基于神经网络的 PDE 求解器,比如忽略了前面 94 年那篇。如果想了解早期的神经网络发展,倒是可以参考 Lu 的一个综述:
Lu, Lu, et al. "DeepXDE: A deep learning library for solving differential equations." SIAM Review 63.1 (2021): 208-228.
好了,先小结一下以上内容。
大家都知道 PINN 是一种(深度)网络,在定义时空区域中给定一个输入点,在训练后在微分方程的该点中产生估计的解。
-
结合对控制方程的嵌入得到残差,利用残差构造损失项就是 PINN 的一项不太新奇的新奇之处了。本质原理就是将方程(也就是所谓的物理知识)集成到网络中,并使用来自控制方程的残差项来构造损失函数,由该项作为惩罚项来限制可行解的空间。 -
用 PINN 来求解方程并不需要有标签的数据,比如先前模拟或实验的结果。从这个角度,对 PINN 在深度学习中的地位进行定位的话,大概是处于无监督、自监督、半监督或者弱监督的地位,这几个不尽相同的说法在不同语境下都有文献提过。 PINN 算法本质上是一种无网格技术,通过将直接求解控制方程的问题转换为损失函数的优化问题来找到偏微分方程解。

连接数据与物理知识
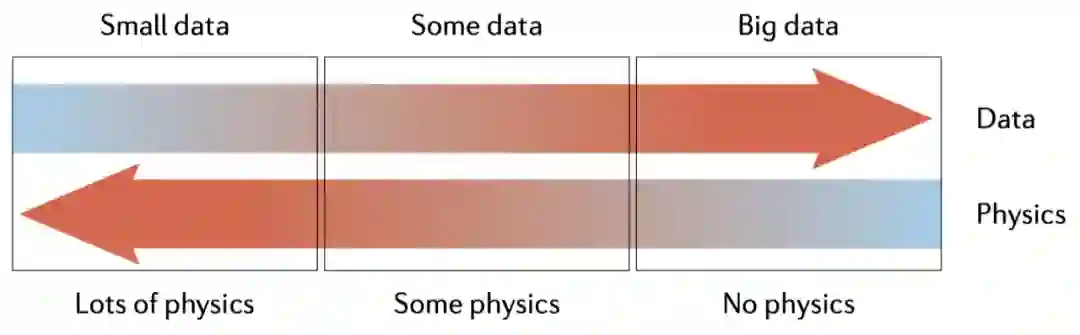
如果把 PINN 当作是单纯的数值求解器,通常来讲,不管从速度或者精度,PINN 在性能上并不能跟传统方法(有限差分、有限元、有限体积等大类方法)抗衡。那么这种方法能火起来必然有其特色,比如 PINN 好就好在这种方法或者思想可以弥补科学机器学习领域中单纯数据驱动的弱点。如果把传统数值格式认为是单纯物理知识驱动,那么 PINN 或者更广义一点的内嵌物理知识机器学习就是数据驱动与知识驱动的融合方法。
先说为什么单纯数据驱动会出问题。首先,纯数据驱动的模型可能非常适合处理大量观测值的应用,但由于外推或观测偏差可能导致泛化性能差,其推断可能并不符合物理,也就是不可信。
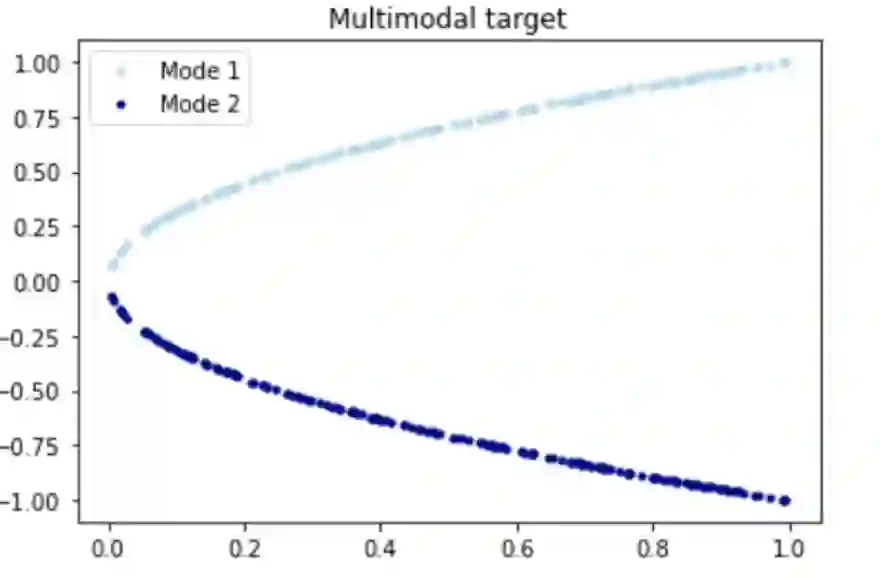
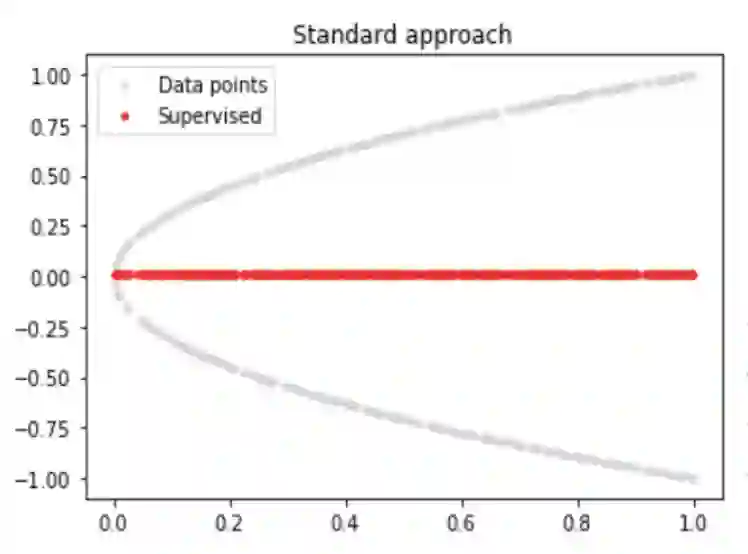
这里加一点吐槽:一些机器学习文章宣称求解 PDE 得到了成百上千倍的加速,其实忽略了大量的数据集生成时间或者网络训练时间,只考虑了推断时间,于是相比传统方法产生了成百上千倍加速。这当然不是说这样做没有应用用途,但作为标题吸引读者然后带来失望对领域发展就不太好了。

基于PyTorch的PINN求解
import torch
# 定义区域及其上的采样
def interior(n=1000):
x = torch.rand(n, 1)
y = torch.rand(n, 1)
cond = (2 - x ** 2) * torch.exp(-y)
return x.requires_grad_(True),
y.requires_grad_(True), cond
# 定义内部损失
loss = torch.nn.MSELoss()
def gradients(u, x, order=1):
if order == 1:
return torch.autograd.grad(u, x,
grad_outputs=torch.ones_like(u),
create_graph=True,
only_inputs=True, )[0]
else:
return gradients(gradients(u, x), x,
order=order - 1)
def l_interior(u):
x, y, cond = interior()
uxy = u(torch.cat([x, y], dim=1))
return loss(gradients(uxy, x, 2) -
gradients(uxy, y, 4), cond)同理构造其他六个区域上的损失函数,这里就不详细展开了,后面附有完整代码的链接:
-
l_down_yy -
l_interior -
l_down_yy -
l_up_yy -
l_down -
l_up
然后就可以构造出总的损失函数:
之后就可以利用 Adam 啊之类的训练求解了。
u = MLP()
# neuron number 2, 32, 32, 32, 32, 1
# with tanh()
opt = torch.optim.Adam(params=u.parameters())
for i in range(10000):
opt.zero_grad()
l = l_interior(u) \
+ l_up_yy(u) \
+ l_down_yy(u) \
+ l_up(u) \
+ l_down(u) \
+ l_left(u) \
+ l_right(u)
l.backward()
opt.step()xc = torch.linspace(0, 1, 100)
xx, yy = torch.meshgrid(xc, xc)
xx = xx.reshape(-1, 1)
yy = yy.reshape(-1, 1)
xy = torch.cat([xx, yy], dim=1)
u_pred = u(xy)
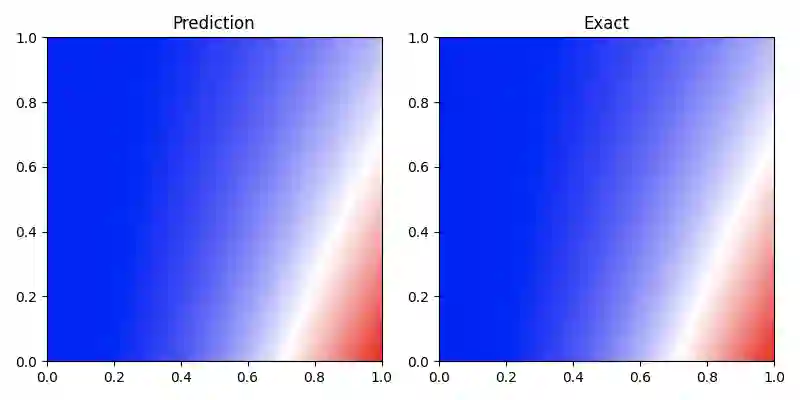
print("Max abs error is: "), print(float(torch.max(torch.abs(u_pred - xx * xx * torch.exp(-yy)))))最后经过一段不太短时间的训练,最大误差数量级大概在 1E-3 左右,精度不算太高,速度也不算快,不过即没付出什么格式设计之类的脑力,也没付出调参的体力,性价比还能接受。完整代码可参考:
https://github.com/zwqwo/PINN_scratch/blob/main/PINN.py
-
Wang, Sifan, Yujun Teng, and Paris Perdikaris. "Understanding and mitigating gradient flow pathologies in physics-informed neural networks." SIAM Journal on Scientific Computing 43.5 (2021): A3055-A3081.(参数梯度流的角度) -
Liu, Dehao, and Yan Wang. "A Dual-Dimer method for training physics-constrained neural networks with minimax architecture." Neural Networks 136 (2021): 112-125.(建模为极小极大问题,不断对大损失项进行惩罚) -
Xiang, Zixue, et al. "Self-adaptive loss balanced Physics-informed neural networks for the incompressible Navier-Stokes equations." arXiv preprint arXiv:2104.06217 (2021).(将权重与损失的方差关联,建模为概率模型)

流体力学中的PINN
计算流体力学(Computational Fluid Dynamics,CFD)是各种工程应用中逃不开的学科,说到这个学科,当然不可避免地会遇到 Navier-Stokes(NS)方程(组),或者在一定条件的各类特化数值模型。
对这个方程(或者其简化模型)进行求解已经有了非常多的商业软件,用 PINN 也能求解,但由于前面提及的 PINN 高度非线性非凸的本质,直接用于 NS 方程的求解或许并不是 PINN 的强项。
CFD 与其说是计算科学,更像是一门实验科学,需要物理实验数据来对解算的模型进行验证,还面临诸多困难。比如目前已有的各类 CFD 方法并不能很好地融合各类保真数据。在工程模型中,可能还涉及逆问题的求解,也就是边界条件和流体的各种参数未知的情形下,如何通过部分测量数据得到精确的模型参数和流场的重构。再者,CFD 网格质量对结果的影响比较大,计算中网格划分本身也是非常耗时的。最后,目前的 CFD 软件都非常庞大,比如 OpenFoam,对每一类问题都有专门的求解模块,拥有超过 10 万行的科学计算代码,其更新与维护也是一件难事。
刚好,PINN 有部分解决以上问题的能力。PINN 对各种数据的融合是非常自然的,不管是压强标量场的时空散点数据、速度矢量场的时空散点数据,还是示踪粒子的运动轨迹,都可以非常容易地融合到 PINN 的求解中。正如前文所提及的,对于 PINN 来讲,求解正问题与求解包含数据的逆问题在形式上并没有太大区别,这是它的巨大优势之一。PINN 作为一种无网格方法,也不需要网格(当然对应的如何选配点是个别的问题)。最后,PINN 的算法核心相对简单,只要 NS 方程能够描述,都能使用统一的形式进行处理,在更新和维护上也是相对容易的。
从以上的对比就可以发现 PINN 这种方法的“甜区”了,即在时空散点测量数据比较充足的情况下,进行 CFD 相关的参数估计、流场重建、代理模型构建等问题的求解。与传统的 CFD 求解器相比,PINN 在集成数据(流量的观测值)和物理知识(其实就是描述该物理现象的控制方程)方面更胜一筹。
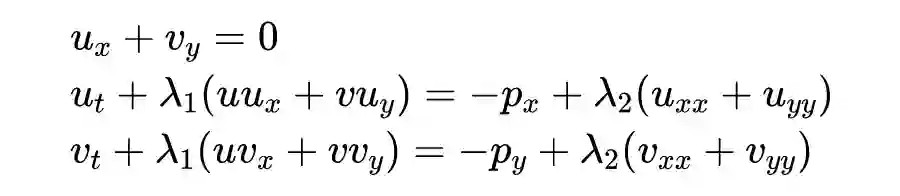
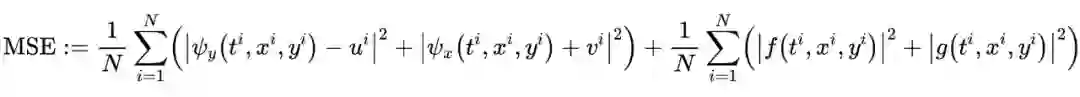
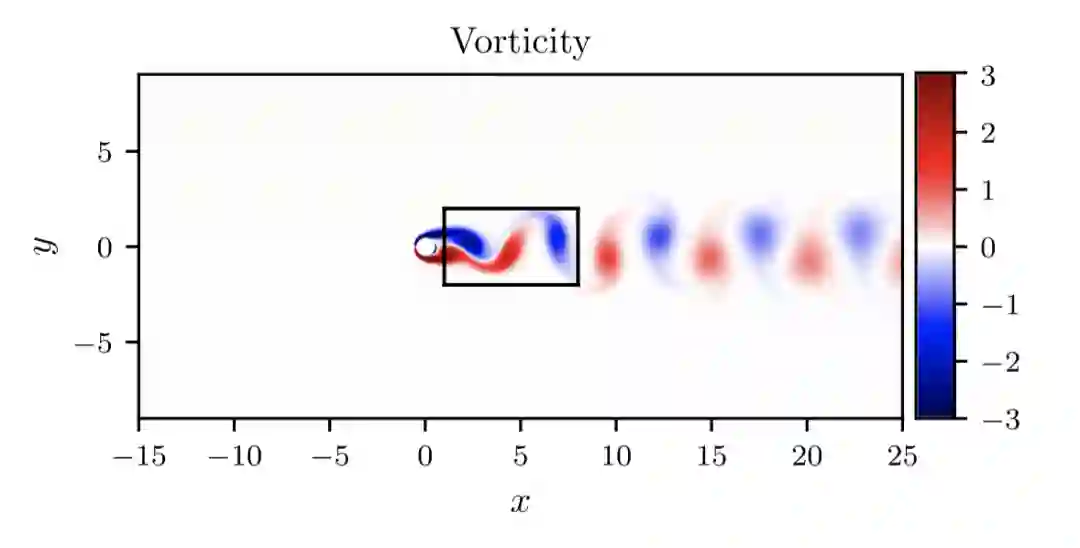
以上是一个比较初步的 PINN 在流场参数恢复中的作用,是 Raissi 在 17 年底文章中的例子。而后,又有了一系列工作。一个比较有前景的应用是流场可视化技术,从观察结果中推断出流场。
比较直接的是通过速度观测来重建全流场。在气动力学等学科的实验研究中,可以利用光学设备,通过粒子图像测速(Particle Image Velocimetry,PIV)和Particle Tracking Velocimetry(PTV)方法测量的得到多个散点速度。然而散点速度并不能满足需求,高分辨率的速度场对于可视化和后续分析是必不可少的。一个非常自然的想法就是通过类似图像插值来实现从散点到高分辨率流场的“超分辨”,但是这种方式处理得到的结果可能“并不符合物理规律”。
作为融合了物理知识的 PINN 方法,可以非常自然地从这些稀疏速度信息来重建分辨率的整体速度场。也就是极小化 NS 方程的损失项,同时得到速度场和压强场,使结果符合“物理规律”。PINN 在扩展 PIV/PTV 功能方面具有一定潜力:
Wang, Hongping, Yi Liu, and Shizhao Wang. "Dense velocity reconstruction from particle image velocimetry/particle tracking velocimetry using a physics-informed neural network." Physics of Fluids 34.1 (2022): 017116.
Raissi, Maziar, Alireza Yazdani, and George Em Karniadakis. "Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations." Science 367.6481 (2020): 1026-1030.

前面已经多次提及了,PINN 需要求解一个高度非线性、非凸的最优化问题,而且涉及到对输入变量的高阶自动微分,其实际求解速度与精度都不太够看。对于有一定数值计算背景的研究者,刚入手 PINN,或许会感慨这么慢的方法为何会存在。再加上正问题和逆问题对于 PINN 来讲,在问题形式上并没有太大区别,很多发表的文章只有正问题的求解案例,可能会导致产生一种 PINN 完全不如传统方法的感觉。前面已经提及了,PINN 的优势不再正问题求解上的速度和精度,而是在于融合数据和知识。
区域分解
融合传统格式
-
浅层网络
区域分解(Domain Decomposition)。在 PDE 的数值求解中,可能会遇到区域较复杂的问题。单个神经网络能表达的容量也是有极限的,要在更复杂的区域上对解进行表达,要么增大网络,也就是在一个网络上增加深度和宽度,但对 PINN 通常使用的 MLP 进行这样的操作可能会带来梯度爆炸或者梯度消失之类的问题,使得求解变得更为困难。因此,借用传统 PDE 求解中区域分解技术,让不同的网络对不同的区域进行学习,从而降低单个神经网络需要的复杂度和学习难度。
从并行计算的角度,将区域分解与 PINN 结合可以非常灵活地处理多尺度问题,充分利用硬件来进行并行实现,分配给不同的 GPU。通信成本的话,就看怎么设计算法了。如何让神经网络之间进行高效信息传递,最终合成可行解,这也是这类算法开发的关键所在。
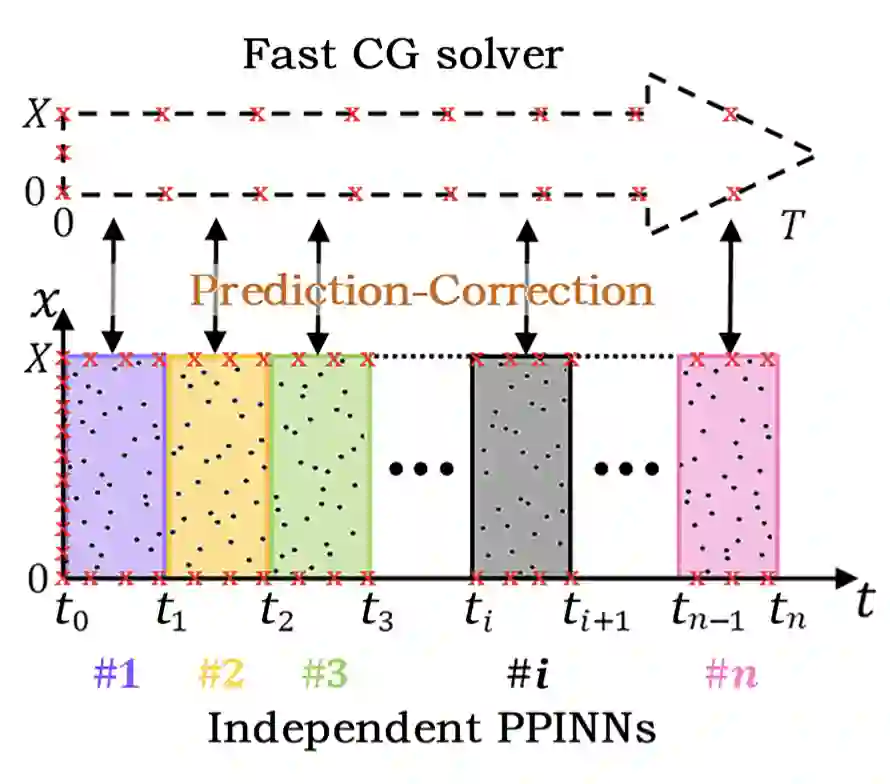
比如利用传统 Parareal 时域分割的方法进行并行化:
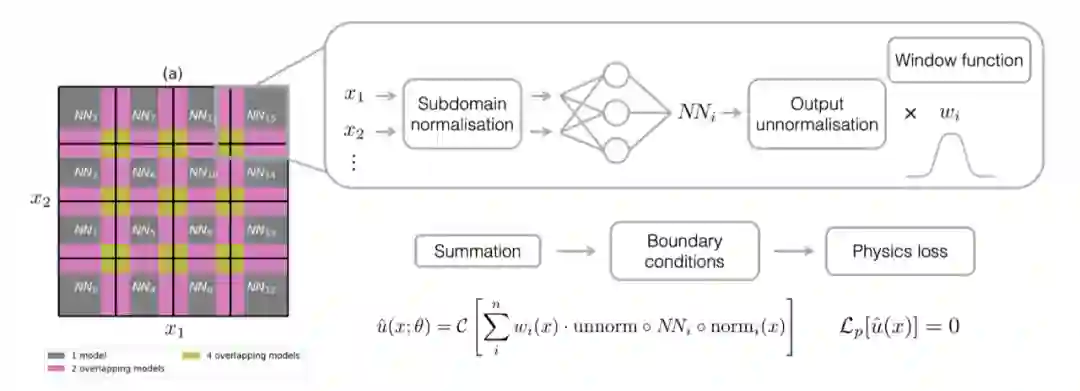
又比如空间上区域分割的并行方法:
如果把思维再往上提一层,所谓的分解,就是为了降低单个神经网络学习的复杂度。那么不仅可以从时空关系上,还可以对微分的阶数进行分解来降低复杂度,避免对单个神经网络求高阶导数:
对于一般的 PINN,其信息的矫正依赖于单点局部导数信息损失的反馈,这种依赖于单点的局部信息传播可能减速了 PINN 的训练。而(通常的)差分格式可以利用多点的局部信息,在多重网格方法下,其信息传播的速度还能得到加速,但差分格式需要均匀网格,对于较为复杂的边界,有限差分方法需要对边界进行逼近处理,过程比较繁琐繁琐而且会引入误差,这也是差分方法的最大局限之一。PINN 作为一种无网格方法,并不需要网格。因此,目前也出现了利用融合差分格式来加速信息传播的算法。比如:
Chen, Yuntian, et al. "Theory-guided hard constraint projection (HCP): A knowledge-based data-driven scientific machine learning method." Journal of Computational Physics 445 (2021): 110624.
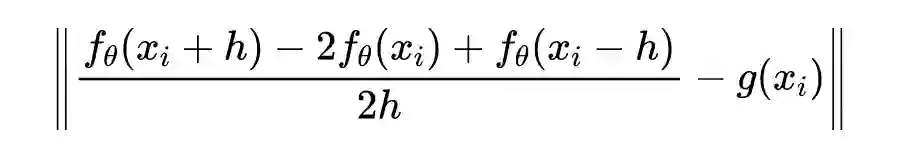
当然,融合网格方法与无网格方法也并不是什么新思想,如果回顾一下稍早的文章,就会发现这种融合有限差分格式(Hybrid Finite Difference,HFD)的技术已经被用于传统的无网格方法了:
Wen, P. H., and M. H. Aliabadi. "A hybrid finite difference and moving least square method for elasticity problems." Engineering analysis with boundary elements 36.4 (2012): 600-605.
提及 PINN,不少文献的综述里通常会把它归类到 Deep Learning 中,也就是需要多层的神经网络,多层的网络是造成 PINN 本身非线性非凸难以求解的主要原因。为了更快速地求解 PINN,又有研究者将目光放回到浅层网络中,也就是结合了极限学习机(Extreme Learning Machine,简称 ELM)的内嵌物理知识极限学习机(Physics Informed ELM,简称 PIELM),这种方法看起来非常粗暴,就一个隐藏层,而且隐藏层的输入参数进行随机初始化后被固定不再需要更新:
对比一下概念,其实也就是之前已经提到了 Kansa 无网格方法,或者 RBF-net 本身也算是一种浅层网络,PIELM 正是其后续发展的回溯,大概也符合否定之否定规律吧。
对于线性方程,可以看出 PIELM 仍然是线性的,也就是跟 Kansa 方法一致,采样后可以通过求解线性方程组或者线性最小二乘问题进行求解,这不用多想,可以猜到会比 PINN 的训练快很多。
非典型应用
相信大家已经对 PINN 已经在求解各种物理场仿真问题的应用有了一些印象。然而下一个内嵌物理又何必是物理?下面列举一些比较稍微比较少见的应用例子,仅用来说明 PINN 在传统物理场仿真之外的用途。
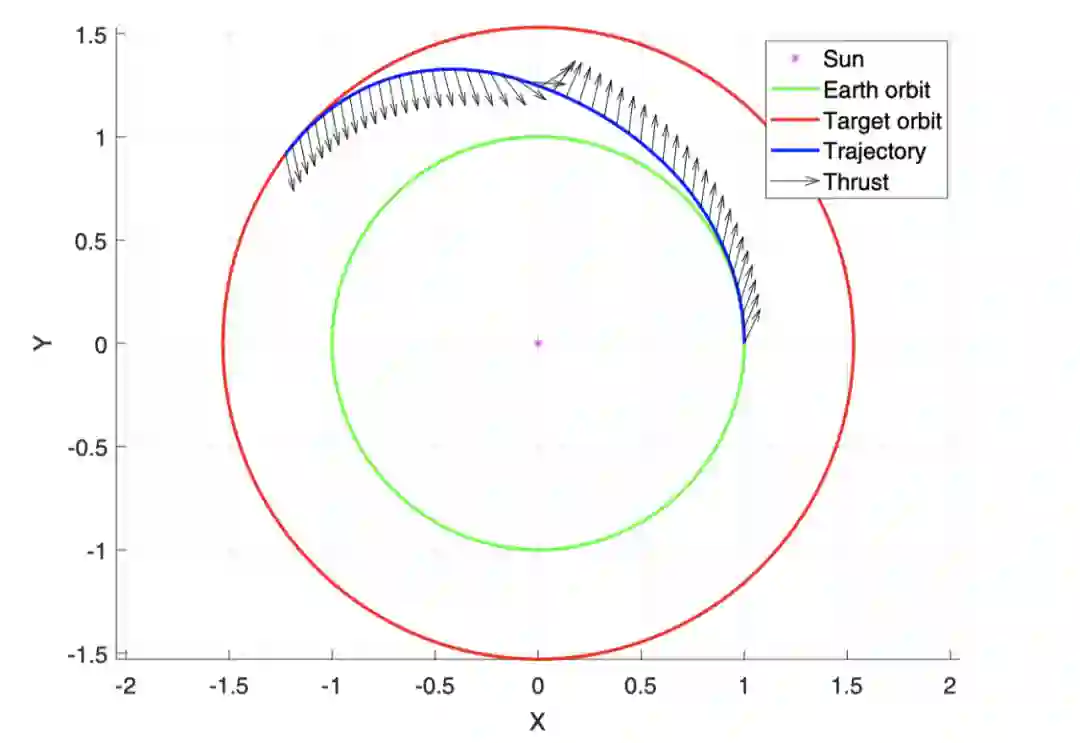
反过来说动力如果充足的话, 大概跟科幻片一样对准目标,然后“咻”一下就飞过去了,不用绕这些弯了。当飞行器从一颗行星轨道(比如地球)转移到另一颗行星轨道(比如火星)时,发射时机和轨道就需要特殊选择和设计优化。但不管事情有多复杂,总得遵循天体力学的运作原理,这些原理又被列成了方程,那么这些方程也就可以被作为物理知识嵌入到神经网络中了。比如这篇文章:
Schiassi, Enrico, et al. "Physics-Informed Neural Networks for Optimal Planar Orbit Transfers." Journal of Spacecraft and Rockets (2022): 1-16.
自从 Covid-19 病毒全球爆发以来,对其进行传染模型建模并且声称很快会结束的研究已经比较多了,不知道是模型本身的问题还是模型参数的问题,虽然以往的各种结果时不时打脸。总之,对于传染病模型,比如 Susceptible-Infected-Recovered(SIR)模型及其各种变体,参数的估计可能跟模型本身的样子可能同样重要。下面这篇文章就提出了一种变种模型,并且用 PINN 对模型的参数进行估计:
Treibert, Sarah, and Matthias Ehrhardt. "An Unsupervised Physics-Informed Neural Network to Model COVID-19 Infection and Hospitalization Scenarios." (2021).
众所周知,建模是容易的,关键是其中参数的设定。比如上面的模型一个有 8 个固定参数和 2 个随时间变化的参数,这两个时变的参数就交给 PINN 处理。通过对现有的六个维度的现实数据进行学习,利用可微分编程,结合了一种隐式有限差分格式实现对这两个时变参数的训练和估计。
抛开这个例子本身应用背景和前途不说,这也代表了 PINN 在动力系统参数估计中一些用途。
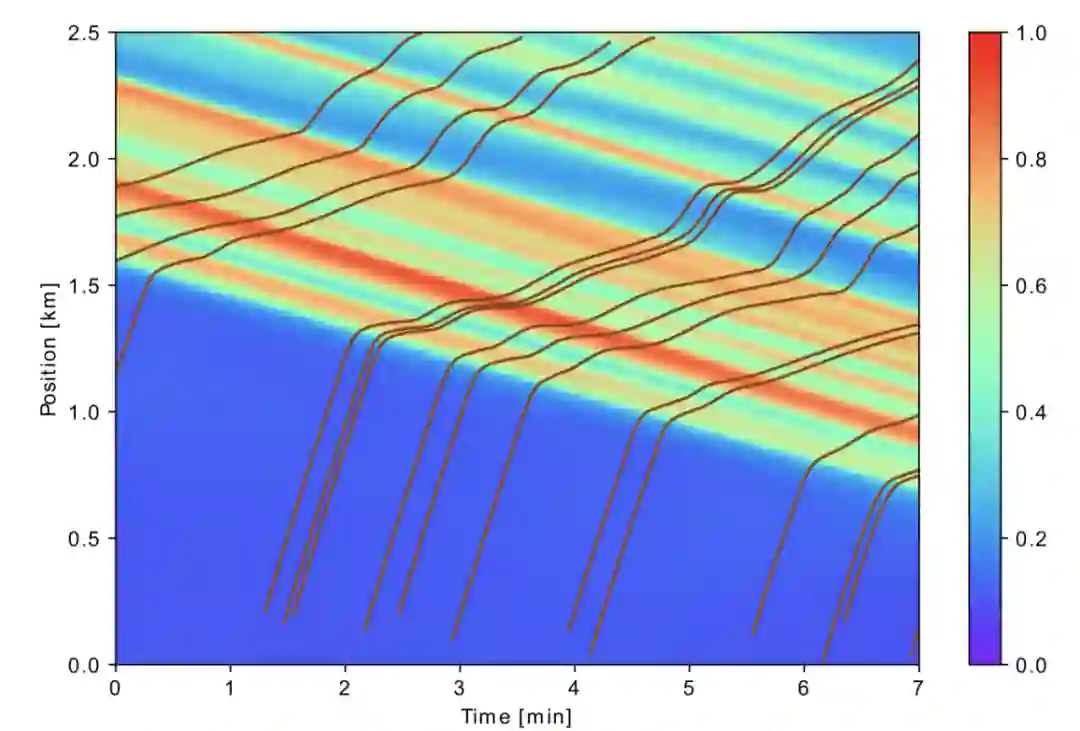
Barreau, Matthieu, et al. "Physics-informed learning for identification and state reconstruction of traffic density." arXiv preprint arXiv:2103.13852 (2021).
推断的图像显式了红色的高密度堵车处在后移,其上的曲线就是所谓的探测车辆轨迹,在密度高的地方会减速。

PINN的求解库
-
DeepXDE,布朗大学 Lu 博士开发的,就是 DeepONet 那位 Lu 博士。他们组是本次 PINN 潮流的先驱,应该算是第一款也是“官方”的 PINN 求解器。集成了基于残差的自适应细化(RAR),这是一种在训练阶段优化残差点分布的策略,即在偏微分方程残差较大的位置添加更多点。还支持基于构造实体几何 (CSG) 技术的复杂几何区域定义。 -
NeuroDiffEq,基于 PyTorch。NeuroDiffEq 通过硬约束来构造 NN 满足初始/边界条件,细分下来叫 PCNN(Physics Constrained Neural Network),由于要设计特定的边界,这种方式会受限于对边界的具体形式。 -
Modulus,Nvidia 公司发布的,之前叫做 SimNet,既然是显卡公司开发的,那么或许可以期待有比较好的硬件性能优化大型工业算例。 -
SciANN,基于 Keras 包封装的实现的。SciANN 里面有比较丰富的应用示例,包括弹性、结构力学和振动应用等。基于这个库有了不少文章。 -
NeuralPDE.jl,看名字就知道是基于 Julia 语言开发的,是 SciML 大项目的一部分。 -
ADCME,基于 TensorFlow 开发的,有一些非线性方程的例子,比如非线性弹性、NS 问题和 Burgers 方程。 -
TensorDiffEq,看名字就知道是基于 Tensorflow,特点是做分布式计算。主旨是通过可伸缩(scalable)计算框架来求解 PINN,明显是为大规模工业应用做铺垫。 -
IDRLnet,国内团队发布的基于 Pytorch 和 sympy 的开源求解器,包含了鲁棒参数估计、变分极小化问题(比如极小曲面计算)、积分方程求解、参数化代理模型等基础算例。 -
Elvet,可以求解 PDE 和变分极小化问题(如悬链线计算)的 Python 库。 -
Nangs,Python 框架,貌似没有更新了。 PyDEns,一个小型框架,貌似没有更新了。

未来
最后再谈谈未来吧。
首先,某些高维偏微分方程的数值求解在物理、工程和金融等各个学科的应用中具有重要意义,PINN 和其他使用物理先验知识的深度学习方法,由于有压缩表示能力,很可能成为解决高维偏微分方程的一种有效方法。
其次,作为“没有免费午餐”定理的一个方面,作为一种“通用方法”,与为特定偏微分方程设计的传统数值格式相比,PINN 在近似偏微分方程数值解的精度和速度方面仍然处于劣势。因此与传统格式的融合(Hybrid)、利用传统格式来加速 PINN 训练的各种研究也在如火如荼进行中。
参考文献
[1] Thuerey, Nils, et al. "Physics-based Deep Learning." arXiv preprint arXiv:2109.05237 (2021).
[2] Cai, Shengze, et al. "Physics-informed neural networks (PINNs) for fluid mechanics: A review." Acta Mechanica Sinica(2022): 1-12.
[3] Karniadakis, George Em, et al. "Physics-informed machine learning." Nature Reviews Physics 3.6 (2021): 422-440.
[4] Lu, Lu, et al. "DeepXDE: A deep learning library for solving differential equations." SIAM Review 63.1 (2021): 208-228.
[5] Cuomo, Salvatore, et al. "Scientific Machine Learning through Physics-Informed Neural Networks: Where we are and What's next." arXiv preprint arXiv:2201.05624 (2022).
特别鸣谢
感谢 TCCI 天桥脑科学研究院对于 PaperWeekly 的支持。TCCI 关注大脑探知、大脑功能和大脑健康。
更多阅读



#投 稿 通 道#
让你的文字被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个,让知识真正流动起来。
📝 稿件基本要求:
• 文章确系个人原创作品,未曾在公开渠道发表,如为其他平台已发表或待发表的文章,请明确标注
• 稿件建议以 markdown 格式撰写,文中配图以附件形式发送,要求图片清晰,无版权问题
• PaperWeekly 尊重原作者署名权,并将为每篇被采纳的原创首发稿件,提供业内具有竞争力稿酬,具体依据文章阅读量和文章质量阶梯制结算
📬 投稿通道:
• 投稿邮箱:hr@paperweekly.site
• 来稿请备注即时联系方式(微信),以便我们在稿件选用的第一时间联系作者
• 您也可以直接添加小编微信(pwbot02)快速投稿,备注:姓名-投稿
△长按添加PaperWeekly小编
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧