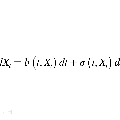Brown运动及分数Brown运动驱动的随机动力系统的概周期性、概自守性及遍历性研究

项目名称： Brown运动及分数Brown运动驱动的随机动力系统的概周期性、概自守性及遍历性研究

项目编号： No.11301090

项目类型： 青年科学基金项目

立项/批准年度： 2014

项目学科： 数理科学和化学

项目作者： 曹俊飞

作者单位： 广东第二师范学院

项目金额： 23万元

中文摘要： 概周期性、概自守性及遍历性等定性性质的研究一直是微分方程及动力系统理论和应用研究中一个既重要而又基本的问题。 本项目基于Guass过程驱动的随机微分方程的概周期性及概自守性研究，进一步研究不同来源，不同统计特性的Guass过程驱动的随机微分方程及其产生的随机动力系统的随机概周期型解和随机概自守型解的存在性、稳定性、几何结构和性质，以及概周期性、概自守性和遍历性以及不变测度之间的关系，建立由分数Guass过程驱动的随机微分方程及其产生的随机动力系统的概周期性、概自守性及遍历性理论。 并由此比较Gauss过程及分数Guass过程驱动的随机微分方程及其产生的随机动力系统的动力学性质异同，分析和讨论随机微分方程及随机动力系统与确定性微分方程及确定性动力系统的动力学行为的本质区别，研究随机因素给微分方程及微分动力系统带来的新问题和新现象。

中文关键词： Brown运动及分数Brown运动；随机微分方程；随机动力系统；确定微分动力系统；动力学性质

英文摘要： The qualitative properties such as almost periodicity, almost automorphy and ergodicity are always the basic and important problem of the theory and application of differential equations and dynamical systems. Based on the almost periodicity, almost automorphy of random stochastic differential equations driven by Gaussian process, we futher study the existence, stability, geometric structure and properties of almost periodic solution, almost automorphic solution, and the relationship between the almost periodicity, almost automorphy and ergodicity of stochastic differential equations and random dynamical systems driven by Gaussian process of different sources and statistical properties. Furthermore, we establish the theory of the almost periodicity, almost automorphy and ergodicity of stochastic differential equations and random dynamical systems driven by frational Gaussian process. Then we compare the qualitative properties of stochastic differential equations and random dynamical systems driven by Gaussian process and frational Gaussian process, analyze the essential difference between stochastic differential equations，random dynamical systems and deterministic differential equations，deterministic dynamical systems, and study the new problems and phenomena of differential equations and dynamical systems

英文关键词： Brown motion and fractional Brown motion；Stochastic differential equations；Random dynamical systems；Deterministic differential dynamical systems；Dynamical properties