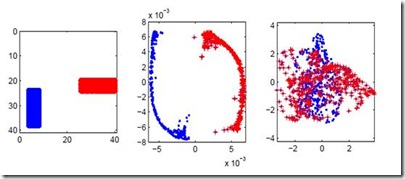
We propose a new nonlinear embedding -- Piecewise Flat Embedding (PFE) -- for image segmentation. Based on the theory of sparse signal recovery, piecewise flat embedding attempts to recover a piecewise constant image representation with sparse region boundaries and sparse cluster value scattering. The resultant piecewise flat embedding exhibits interesting properties such as suppressing slowly varying signals, and offers an image representation with higher region identifiability which is desirable for image segmentation or high-level semantic analysis tasks. We formulate our embedding as a variant of the Laplacian Eigenmap embedding with an $L_{1,p} (0<p\leq1)$ regularization term to promote sparse solutions. First, we devise a two-stage numerical algorithm based on Bregman iterations to compute $L_{1,1}$-regularized piecewise flat embeddings. We further generalize this algorithm through iterative reweighting to solve the general $L_{1,p}$-regularized problem. To demonstrate its efficacy, we integrate PFE into two existing image segmentation frameworks, segmentation based on clustering and hierarchical segmentation based on contour detection. Experiments on four major benchmark datasets, BSDS500, MSRC, Stanford Background Dataset, and PASCAL Context, show that segmentation algorithms incorporating our embedding achieve significantly improved results.
翻译:我们提出一个新的非线性嵌入(PFE) -- -- Papfise Flat 嵌入(PFE) -- -- 新的非线性嵌入(PFE) -- -- 用于图像分割。根据信号恢复少的理论,平平地嵌入(PFE)尝试(PFE),以恢复一个带稀疏区域边界和聚集值分散的零点常态图像常态图像代表。由此产生的平面嵌入(PFEE),以恢复一个带稀疏区域边界和分散的聚集值分布式图像常态(PFFE)代表(PFEE),以图解(PFEEE Eigenmap) 嵌入($L ⁇ 1,p}(0 <pleqq1) ) 的变异种。首先,我们设计了一个基于 Bregman 迭代碼的双阶段数字算($L1,}固定的平面缩嵌化(PSAS) 数据,我们进一步将这种算法概括化为解决一般的 $L1($1,PL1,p} 常规问题。为了展示其效率,我们将PFEFEFEFE 将PEBSDSBSDAR rolaldealdealdealdealaldealisalisal laved laction) 数据定位,在BDS 上,在BDS 上,在BDS AS AS AS AS 上大幅显示。