【泡泡读者来稿】VINS 论文推导及代码解析(一)
总体框架
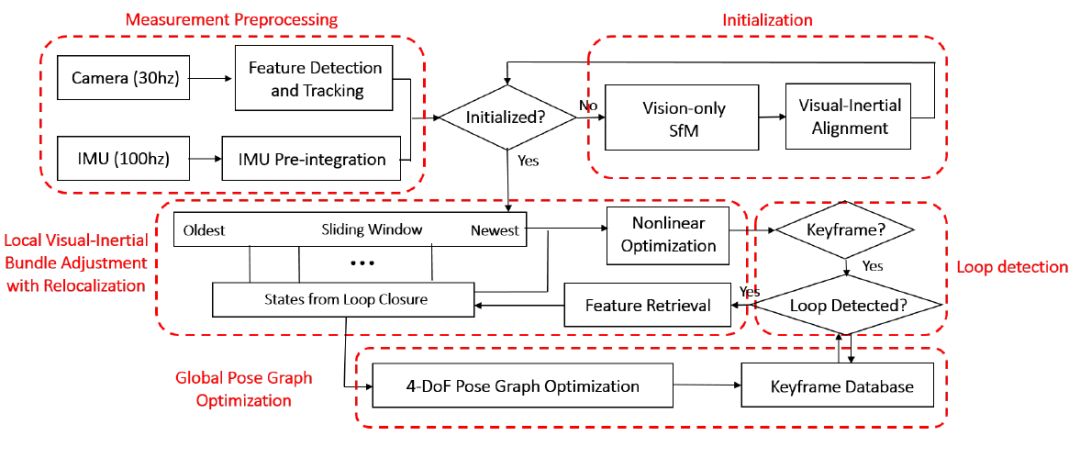
VINS 的功能模块可包括五个部分:数据预处理、初始化、后端非线性优化、闭环检测
及闭环优化。代码中主要开启了四个线程,分别是:1)前端图像跟踪 2)后端非线性优化(其中
初始化和 IMU 预积分在这个线程中) 3)闭环检测 4)闭环优化。
各个功能模块主要有如下作用。
图像和 IMU 预处理
图像:提取图像 Harris 角点,利用金字塔光流跟踪相邻帧,通过 RANSAC 去除异常点,最后将跟踪到的特征点 push 到图像队列中,并通知后端进行处理。
IMU:将 IMU 数据进行积分,得到当前时刻的位置、速度和旋转(PVQ),同时计算在后端优化中将用到的相邻帧的预积分增量,及预积分误差的 Jacobian 矩阵和协方差项。
初始化
首先,利用 SFM 进行纯视觉估计滑窗内所有帧的位姿及 3D 点逆深度,最后与 IMU 预积分进行对齐求解初始化参数。
后端滑窗优化
将视觉约束、 IMU 约束和闭环约束放在一个大的目标函数中进行非线性优化,求解滑窗内所有帧的 PVQ、bias 等。
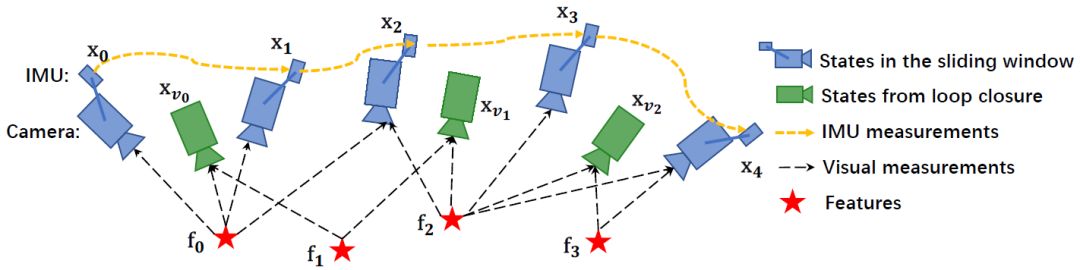
闭环检测和优化
利用 DBoW 进行闭环检测,当检测成功后进行重定位,最后对整个相机轨迹进行闭环优
化。
IMU 预积分
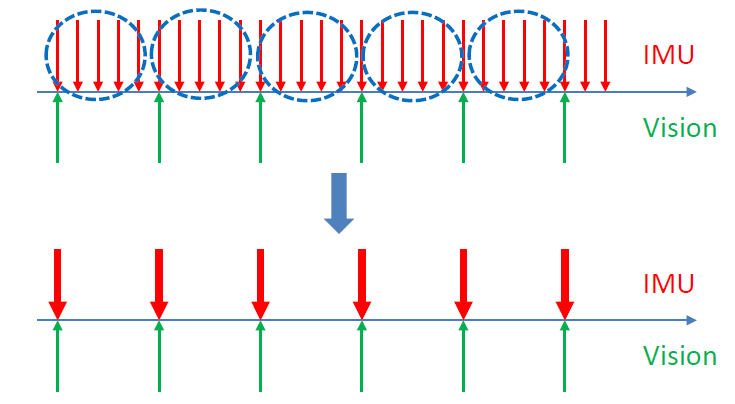
当前时刻 PVQ 的连续形式
将第 k 帧和第 k+1 帧之间的所有 IMU 进行积分,可得第 k+1 帧的位置、速度和旋转(PVQ),作为视觉估计的初始值,这里的旋转采用的四元数。
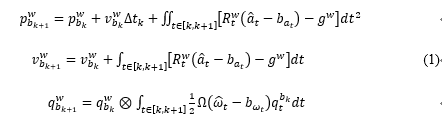
其中,hat a_t , hat omega_t 和为IMU测量的加速度和角速度,是在Body自身坐标系,world坐标系是IMU所在的惯导系,上式的旋转公式推导后期会提供参考附录。
当前时刻PVQ的连续形式
将第k帧和第k+1帧之间的所有IMU进行积分,可得第k+1帧的位置、速度和旋转(PVQ),作为视觉估计的初始值,这里的旋转采用的四元数。
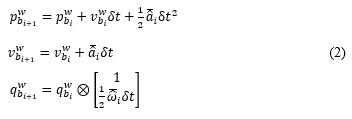
其中:
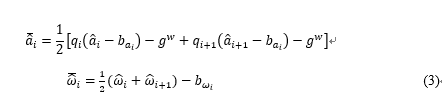
两帧之间PVQ增量的
连续形式
通过观察公式(1)可知,IMU的预积分需要依赖与第k帧的v和R,当我们在后端进行非线性优化时,需要迭代更新第k帧的v和R,这将导致我们需要根据每次迭代后值重新进行积分,这将非常耗时。因此,我们考虑将优化变量从第k帧到第k+1帧的IMU预积分项中分离开来,通过对公式(1)左右两侧各乘 R_w^{b_k} ,可化简为:
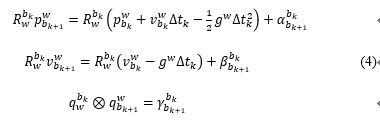
其中:
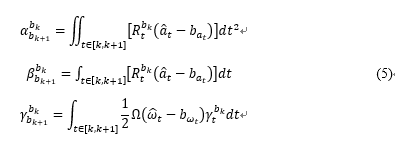
这样我们就得到了连续时刻的IMU预积分公式,可以发现,上式得到的IMU预积分的值只与不同时刻的 hat a_t 和 hat omega_t 相关。
这里我们需要重新讨论下公式(5)的预积分公式,以 hat alpha_{b_{k+1}}^{b_k} 为例,我们发现它是与IMU的bias相关的,而bias也是我们需要优化的变量,这将导致的问题是,当每次迭代时,我们得到一个新的bias,又得根据公式(5)重新对第k帧和第k+1帧之间的IMU预积分,非常耗时。这里假设预积分的变化量与bias是线性关系,可以写成:
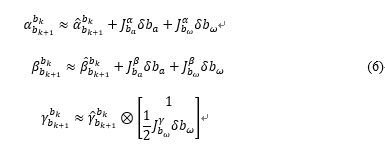
两帧之间PVQ增量的
欧拉法离散形式
下面给出离散时刻的IMU预积分公式,首先按照论文中采用的欧拉法,给出第i个IMU时刻与第i+1个IMU时刻的变量关系为:
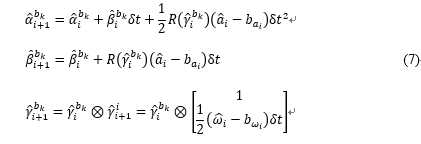
下面给出代码中采用的基于中值法的IMU预积分公式,这与Estimator::processIMU()函数中的IntegrationBase::push_back()上是一致的。注意这里跟公式(2)是不一样的,这里积分出来的是前后两帧之间的IMU增量信息,而公式(2)给出的当前帧时刻的物理量信息。
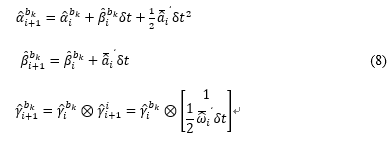
其中,
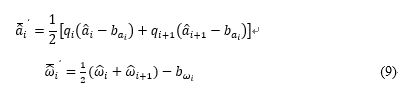
连续形式下PVQ增量的
误差、协方差及Jacobian
IMU在每一个时刻积分出来的值是有误差的,下面我们对误差进行分析。首先我们直接给出在t时刻误差项的导数为:
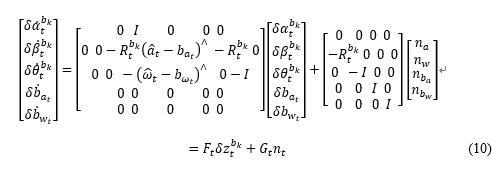
其中,
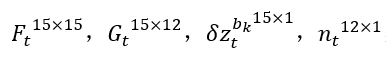
上式推导可参考附录。下面我们讨论它的作用,将其可以简写为:
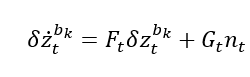
根据导数定义可知:
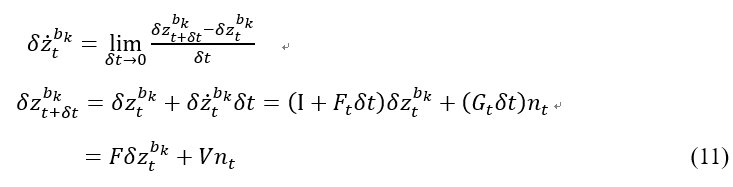
为了简化下一节中对离散形式的分析,上式中我们令
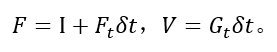
这里我们对公式(11)的IMU误差运动方程再说明,将上式和EKF对比可知,上式恰好给出了如EKF一般对非线性系统线性化的过程,这里的意义是表示下一个时刻的IMU测量误差与上一个时刻的成线性关系,这样我们根据当前时刻的值,可以预测出下一个时刻的均值和协方差,而公式(11)给出的是均值预测,协方差预测公式如下:
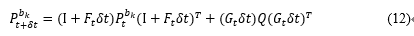
上式给出了协方差的迭代公式,初始值 P_{b_k}^{b_k}=0 。其中,Q为表示噪声项的对角协方差矩阵:
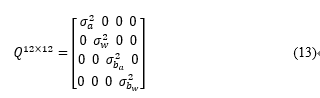
另外根据(11)式可获得误差项的Jacobian的迭代公式:

离散形式的PVQ增量
误差分析
我们首先直接给出PVQ增量误差在离散形式下的矩阵形式,为了与代码一致,我们修改下变量顺序,这和代码中midPointIntegration()函数是一致的。(但不知为何计算的V中与前四个噪声项相关的差个负号?)
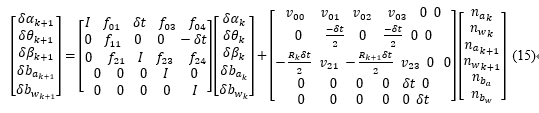
其中,推导可参考附录
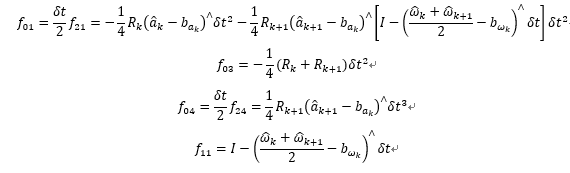
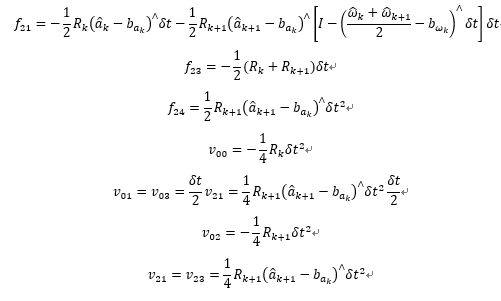
离散形式PVQ增量误差的
Jacobian和协方差
将公式(15)简写为:

则Jacobian的迭代公式为:

其中,Jacobian的初始值为 J_k = I 。这里计算出来的只是为了给后面提供对bias的Jacobian。
协方差的迭代公式为:
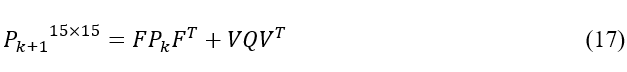
其中,初始值 P_k=0 。Q为表示噪声项的对角协方差矩阵:
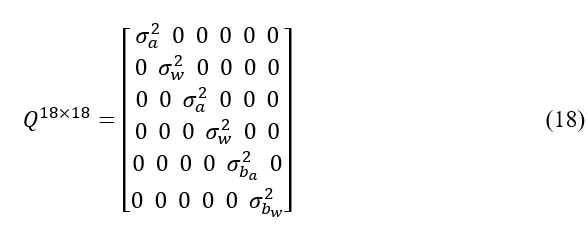
欢迎来到泡泡论坛,这里有大牛为你解答关于SLAM的任何疑惑。
有想问的问题,或者想刷帖回答问题,泡泡论坛欢迎你!
泡泡网站:www.paopaorobot.org
泡泡论坛:http://paopaorobot.org/bbs/


泡泡机器人SLAM的原创内容均由泡泡机器人的成员花费大量心血制作而成,希望大家珍惜我们的劳动成果,转载请务必注明出自【泡泡机器人SLAM】微信公众号,否则侵权必究!同时,我们也欢迎各位转载到自己的朋友圈,让更多的人能进入到SLAM这个领域中,让我们共同为推进中国的SLAM事业而努力!
商业合作及转载请联系liufuqiang_robot@hotmail.com


