【泡泡读者来稿】VINS 论文推导及代码解析（三）

2019 年 3 月 16 日 泡泡机器人SLAM

崔华坤，SLAM算法工程师，主要研究方向是VIO。2011年硕士毕业于北京工业大学，毕业后从事六年的三维显示研发，从最初的裸眼3D显示到现在的AR显示，期间做出一款国内尺寸最大的裸眼3D LED屏。对作者感兴趣的可以加微信:cuihuakun。

六、边缘化Marginalization和FEJ

边缘化和Schur补公式

根据前面讨论的基于高斯牛顿的非线性优化理论可知，可写成如下形式：

值得说明的是，上式中并非一定为相机位姿部分和路标部分，而是希望marg的部分和希望保留的部分。另外，VINS中的边缘化与G2O计算过程中的边缘化意义不大相同（虽然处理方法一致）：G2O中对路标点设置边缘化(pPoint->setMarginalized(true))是为了在计算求解过程中，先消去路标点变量，实现先求解相机位姿，然后再利用求解出来的相机位姿反过来计算路标点的过程，目的是为了加速求解，并非真的将路标点给边缘化掉；而VINS中则真正需要边缘化掉滑动窗口中的最老帧或者次新帧，目的是希望不再计算这一帧的位姿或者与其相关的路标点，但是希望保留该帧对窗口内其他帧的约束关系。

假设上式中的是我们要marg的变量，比如一个相机的pose，因此我们更关心如何只去求解我们希望保留的变量，而不再求解，同时我们又不能直接将和与其相关的路标点等信息直接删除掉，因为这样会减少约束，丢失信息。因此，采用如下Schur进行消元：

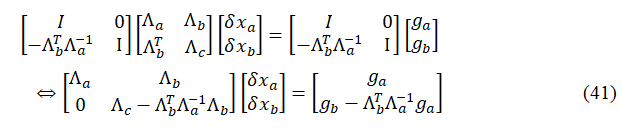
其中，就称为在中的Schur项，那么有了上面式子，我们就可以直接计算了：

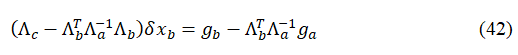
注意上式是从(40)式转化而来，我们并未丢失任何约束，因此不会丢失信息。值得说明的，上面的公式即为要保留变量的先验信息。

一个边缘化的例子

下面我们用一个具体例子来形象说明边缘化过程及其导致的矩阵稠密现象(fill-in)。假设有四个相机位姿，以及6个路标点(路标点用xyz的参数化），相机与路标点的边表示一次观测，相邻相机之间的边表示IMU约束，相互关系如下：

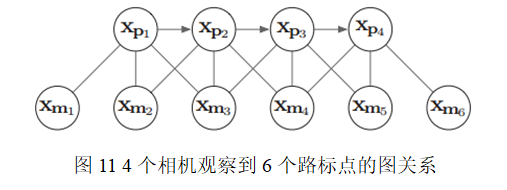
下面试图将给marg掉，然后再将给marg掉，看看H矩阵会如何变化。

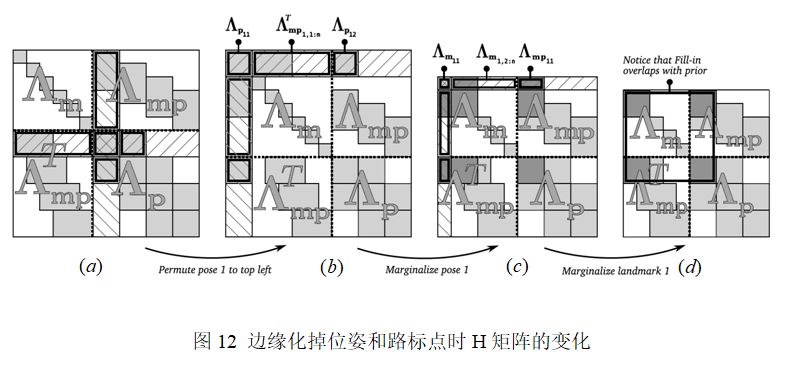
下面我们对上图进行详细说明，图(12-a)表示原始的H矩阵，注意这里的左上角为路标点相关部分，而右下角是pose相关部分。

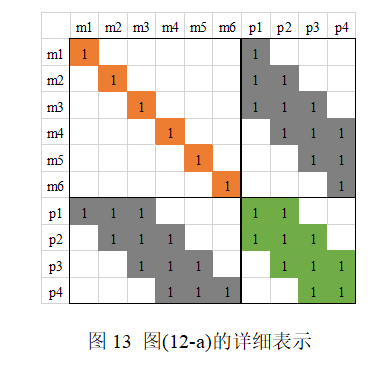
图(12-b)是把H矩阵中跟相关的部分移动到H矩阵左上角。

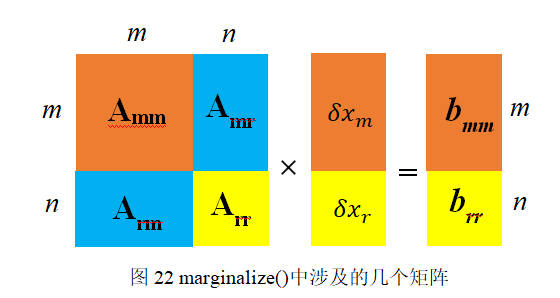
图(12-c)是把边缘掉后的H矩阵，实际上就是(42)式中对应的。这里详细说明下，我们从上面(40)式进行说明，这里的，

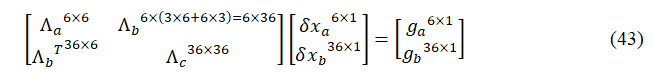
其中各矩阵的维度已在上式标明，也就是说图(12-c)的矩阵大小为36×36。我们可以看到，图(c)相对于图(b)变得更稠密了，即marg掉一个pose，会使得剩余的H矩阵有3个地方被fill-in，如图(c)中颜色加重区域。

这时图关系则变为：

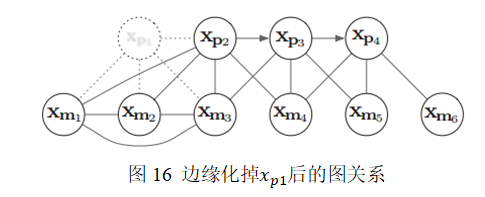
注意，观察图16可发现这时的、和彼此之间已经产生了新的约束关系，且也与产生了新的约束关系。

图(12-d)是marg掉后的H矩阵，详细如下所示：

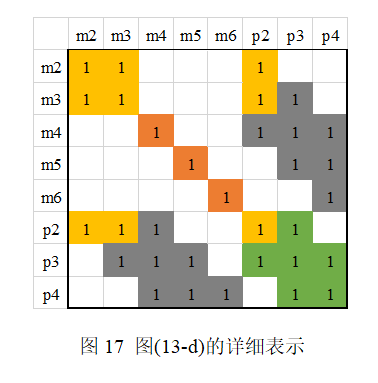
对应的图关系如下：

我们发现，marg掉后，并没有使H矩阵更稠密，这是因为之前并未与其他pose有约束关系，即并未被观察到，因此如果marg掉那些不被其他帧观测到的路标点，不会显著地使H矩阵变得稠密。而要marg掉的路标点中，对于那些被其他帧观测到路标点，要么就别设置为marg，要么就宁愿丢弃，这就是OKVIS中用到的策略。

VINS两种边缘化策略

marginalization_factor.cpp代码中有几个变量需要提前说明：

举例说明，当第一次marg掉最老帧时，parameter_block_size为所有变量及其对应的localSize，parameter_block_data为对应的数据（double*类型）。下面举例说明，假设最老帧即第0帧看到了k=68个路标点，那么代码中的parameter_block_size或parameter_block_data两个vector的大小均为：

pos=所有变量总localSize为：9×2 + 6×11 + 6 + 1 + 68 = 159

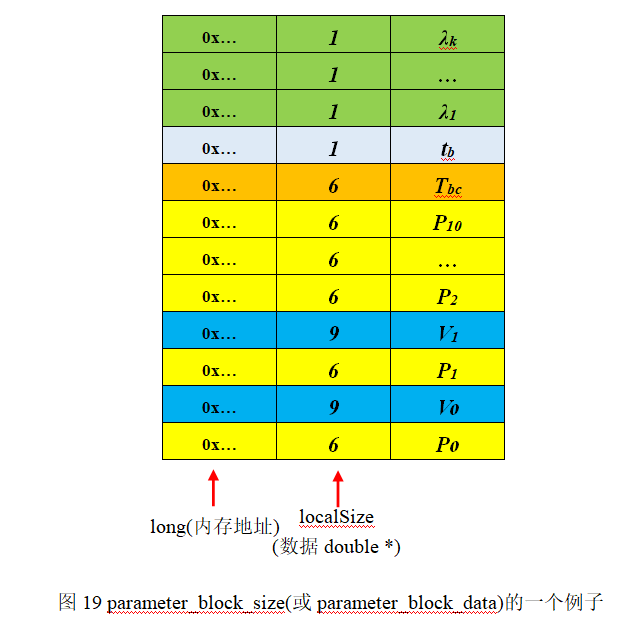
parameter_block_idx为需要marg掉的变量，我们仍然假设第0帧看到k=68个路标点，则parameter_block_idx的数组大小为：

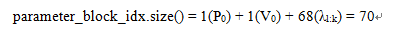
MarginalizationInfo::m表示需marg变量的总localSize，即为：

m = 6 + 9 + 68 = 83

那么，MarginalizationInfo::n表示需保留变量的总localSize为：

n = pos – m = 159 - 83 = 76

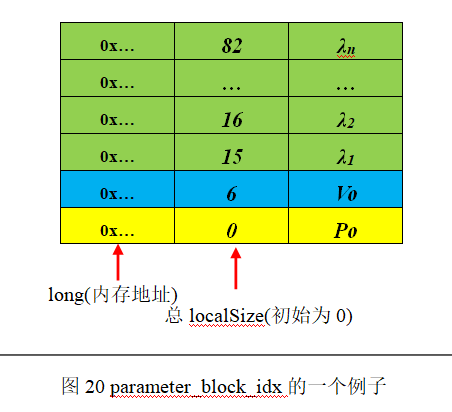
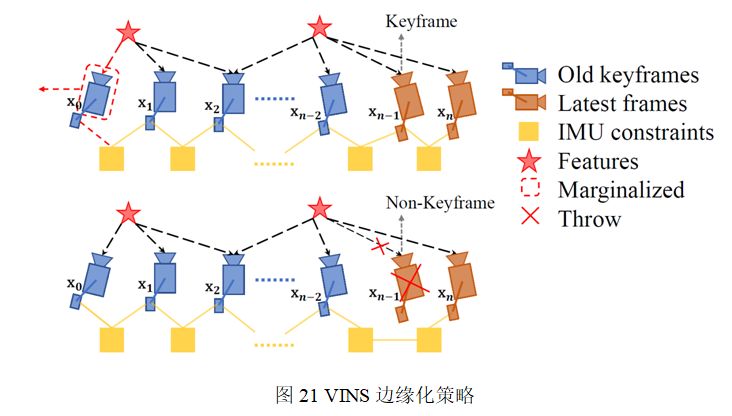
VINS根据次新帧是否为关键帧，分为两种边缘化策略：通过对比次新帧和次次新帧的视差量，来决定marg掉次新帧或者最老帧，对应到Estimator::optimization代码中详细分析：

1.当次新帧为关键帧时，MARGIN_OLD将marg掉最老帧，及其看到的路标点和相关联的IMU数据，将其转化为先验信息加到整体的目标函数中：

1）把上一次先验项中的残差项（尺寸为n）传递给当前先验项，并从中去除需要丢弃的状态量；

2）将滑窗内第0帧和第1帧间的IMU预积分因子（pre_integrations[1]）放到marginalization_info中，即图11中上半部分中x0和x1之间的表示IMU约束的黄色块；

3）挑选出第一次观测帧为第0帧的路标点，将对应的多组视觉观测放到marginalization_info中，即图11中上半部分中x0所看到的红色五角星的路标点；

4）marginalization_info->preMarginalize()：得到每次IMU和视觉观测(cost_function)对应的参数块(parameter_blocks)，雅可比矩阵(jacobians)，残差值(residuals)；

5）marginalization_info->marginalize()：多线程计整个先验项的参数块，雅可比矩阵和残差值，即计算公式(42)，其中与代码对应关系为：

2.当次新帧不是关键帧时，MARGIN_SECOND_NEW，我们将直接扔掉次新帧及它的视觉观测边，而不对次新帧进行marg，因为我们认为当前帧和次新帧很相似，也就是说当前帧跟路标点之间的约束和次新帧与路标点的约束很接近，直接丢弃并不会造成整个约束关系丢失过多信息。但是值得注意的是，我们要保留次新帧的IMU数据，从而保证IMU预积分的连贯性。

通过以上过程先验项就构造完成了，在对滑动窗口内的状态量进行优化时，把它与 IMU 残差项和视觉残差项放在一起优化，从而得到不丢失历史信息的最新状态估计的结果。

First Estimate Jacobian(FEJ)

因为迭代过程中，状态变量会被不断更新，计算雅克比时我们要fix the linearization point。所谓linearization point就是线性化时的状态变量，即求雅克比时的变量，因为计算雅克比是为了泰勒展开对方程进行线性化。我们要固定在点x0(marg时的状态变量)附近去计算雅克比，而不是每次迭代更新以后的x。

但是，VINS中并未使用FEJ的策略，这里我们进行简要说明：对于滑窗内剩余的优化变量，如倒数第二帧位姿T1，当边缘化掉最老帧T0后，会给T1加上新的约束。值得注意的是，这个新约束的线性化点是在marg掉T0时刻的T1的值，而当之后T1迭代更新后，该marg产生的约束并不会调整线性化点，即不会在新的T1处重新展开，这样会导致两次的线性化点不一致。但据作者描述因未发现明显的yaw不可观性变化导致的轨迹漂移，因此并未采用FEJ策略，反而加入FEJ后导致结果不佳。可以结合OC-EKF和MSCKF 2.0等一系列论文对FEJ进行深入研究，这里仅将FEJ的相关知识罗列在此。

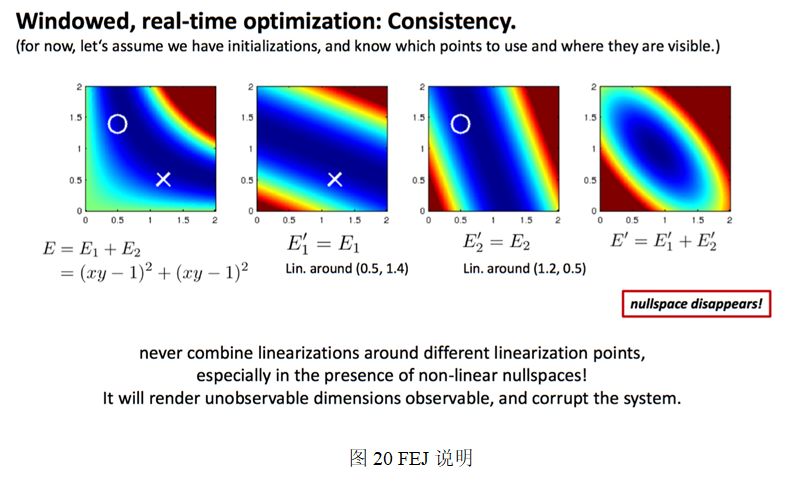
在刘毅(稀疏毅)，王京，晓佳等人讨论下，对这张图作出了如下解释：四张能量图中，第一张是说明能量函数E由两个同样的非线性函数E1和E2组成，我们令函数E=0，这时方程的解为xy=1，对应图中深蓝色的一条曲线。第二张能量函数图中的对应函数E1在点(0.5,1.4)处的二阶泰勒展开，第三张能量函数图中的对应函数E2在点(1.2,0.5)处的二阶泰勒展开。注意这两个近似的能量函数和是在不同的线性点附近对原函数展开得到的。最后一张图就是把这个近似得到的能量函数合并起来，对整个系统E的二阶近似。

从第四个能量函数图中，我们发现一个大问题，能量函数为0的解由以前的一条曲线变成了一个点，不确定性的东西变得确定了，专业的术语叫不可观的状态变量变得可观了，说明我们人为的引入了错误的信息。这个实验的实质在于，在不同的点线性化后，强行加起来，实际上引入了一些人为的约束，或者说引入了人为的“错误观测”，导致整个系统的崩溃。对应到marg的问题上，本来我们是在最初(initial)那个点附近进行线性化，但是在marg的过程，initial那个点变了，它一开始是有未marg的点的，marg之后，把那些点的信息给了留下的那些点，这就使得剩下那些点进行了一些偏移，他们和之前的状态不同了，这个时候再线性化，就会导致在不同的地方进行了线性化，这样就会像上面那个例子一样，引入了错误的信息，导致整个优化过程的崩溃。因此，marg时，被marg的那些变量的雅克比已经不更新了，而此时留在滑动窗口里的其他变量的雅克比要用和marg时一样的线性点，就是FEJ去算，不要用新的线性点了。

未完待续

欢迎来到泡泡论坛，这里有大牛为你解答关于SLAM的任何疑惑。

有想问的问题，或者想刷帖回答问题，泡泡论坛欢迎你！

泡泡网站：www.paopaorobot.org

泡泡论坛：http://paopaorobot.org/bbs/